Решение. Функция f(x) имеет четыре корня (в точках x, равных 1, 4, 7 и 9) и три экстремума в точках x = =2, x = 6

Решение.

Функция f(x) имеет четыре корня (в точках x, равных 1, 4, 7 и 9) и три экстремума в точках x = =2, x = 6, x = 8. Своих экстремумов функция достигает в тех точках, в которых первая производная обращается в нуль. Таким образом, сумма .

Решение.

Для решения задачи найдём значения функции в критических точках внутри заданного отрезка и значения функции на его концах.

. Критические точки x = 11 и x = -1. Внутри данного интервала лежит одна точка x = 11. Вычисляем значения функции: 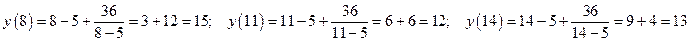. Наименьшее значение функции на данном интервале , наибольшее значение . Следовательно, .

Решение.

Интервалы возрастания-убывания функции определяют с помощью первой производной:

. Производная равна нулю в одной точке (x = 2) и знак производной зависит только от множителя (x - 2) (остальные множители положительны при любом значении x). Поэтому интервал убывания данной функции только один.