Федеральное агентство по образованию РФ
Тверской государственный технический университет
Кафедра «Безопасность жизнедеятельности и экология»
Мониторинг среды обитания
Методические указания
по выполнению расчетно-графической работы
Тверь 2009
Содержание
1. Требования к оформлению РГР………………………………………………….3
2. Методики расчета…………………………………………………………………3
3.Задания для выполнения расчетно-графической работы………………………..7
Требования к оформлению РГР
РГР выполняется в печатном виде на листах формата А4. Текст работы располагается только с одной стороны листа. Курсовая работа печатается шрифтом Times New Roman. Размер шрифта должен быть 14, а междустрочный интервал – полуторный. Размеры полей: правое - 10 мм, верхнее и нижнее - 20 мм, левое - 30 мм.
Методики расчета.
РАСЧЕТ РАЗБАВЛЕНИЯ СТОЧНЫХ ВОД В ВОТОТОКАХ И ВОДОЁМАХ
(Метод Фролова-Родзиллера)
Данный метод получил широкое распространение для больших и средних водотоков.
Основной механизм снижения концентрации загрязняющего вещества при сбросе сточных вод в водные объекты – разбавление. В практике расчетов используют понятие кратность разбавления. Кратность разбавления в водотоке у расчетного створа выражается зависимостью:
 (1)
(1)
где γ – коэффициент смешения, показывающий, какая часть воды водотока участвует в разбавлении; q – максимальный расход сточных вод, м3/с; Q – расчетный максимальный расход воды водотока в контрольном створе, м3/с.
В соответствии с этим методом коэффициент смешения находят по формуле (2):
 (2)
(2)
где L - расстояние по фарватеру водотока от места выпуска до расчетного створа, м; α – коэффициент, зависящий от гидравлических условий смешения:
 (3)
(3)
где ξ – коэффициент, зависящий от расположения выпуска сточных вод в водоток:
при выпуске у берега ξ =1,
при выпуске в фарватер (русловой выпуск) ξ =1,5;
φ – коэффициент извилистости водотока, т.е. отношение расстояния между рассматриваемыми створами водотока по фарватеру к расстоянию по прямой; D – коэффициент турбулентной диффузии:
 (4)
(4)
где g - ускорение свободного падения, м/с2; Cш – коэффициент Шези, м1/2/c, М – коэффициент, зависящий от Cш.
При условии: 10< Cш <60, M = 0,7 Cш + 6;
при Cш ≥600, М = 48 = const.
Произведение МCш имеет размерность м/с2.
При решении задач о распространении и транспорте растворенных и взвешенных веществ в естественных потоках используют уравнение В.М. Маккавеева:
 (5)
(5)
 (6)
(6)
где с – концентрация загрязняющего вещества в воде, мг/л; t - время, с; U – гидравлическая крупность взвешенных веществ, м/с (для растворенных веществ U =0 и уравнение записывается без последнего члена); Vx, Vy, Vz – компоненты скорости течения (м/с) относительно координат х, у, z. Ось х направлена по течению потока, ось у – от поверхности ко дну, ось z – по ширине потока.
Детальные методы решения уравнения турбулентной диффузии, позволяющие получать поле концентрации загрязняющего вещества в пределах всего рассматриваемого участка, от места сброса сточных вод до контрольного створа разработаны А.В. Караушевым.
Уравнение (7) может быть существенно упрощено, например, в случае рассмотрения задачи распространения загрязнения в воде в одной какой-либо плоскости (так называемая плоская задача). Для горизонтальной плоскости уравнение будет выглядеть следующим образом:
 (7)
(7)
Эта задача возникает, в частности, в том случае, когда по вертикальной оси перемешивание загрязняющих веществ с водой происходит очень быстро, поперечные течения отсутствуют и интересно проследить распространение загрязняющих веществ по ширине потока на различных расстояниях от места сброса сточных вод.
Используемые при расчете граничные условия основаны на принципе сохранения вещества, учитывающие, что перенос загрязняющего вещества через поверхность, ограничивающую поток жидкости, равен нулю, т.е. для береговой черты потока граничные условия запишутся в виде:
 (8)
(8)
Поскольку коэффициент D не может равняться нулю (D ≠0), то выражение (9) приобретает вид:
 (9)
(9)
Начальные условия могут задаваться либо в виде распределения концентрации загрязняющего вещества на начальном поперечнике, либо в виде расхода и концентрации поступающего в водный объект загрязняющего вещества с указанием места его поступления.
Уравнение (8) можно записать в форме конечных разностей. Содержащиеся в нем дифференциалы ∂ с, ∂х, ∂z заменяются конечными приращениями ∆с, ∆х, ∆z.
Уравнение (8) приобретает вид:
 (10)
(10)
Для расчета турбулентной диффузии всю расчетную область потока делим плоскостями, параллельными координатным, на расчетные клетки – элементы. По оси х число таких элементов k, по оси z – m. Каждому элементу присваивается свой индекс по соответствующим осям координат.
Изменение индекса на единицу показывает переход от одного элемента к соседнему. Значениям концентрации в каждом элементе присваиваются те же индексы (табл. 1)
Расчетное уравнение, позволяющее определять распространение концентрации загрязняющего вещества по длине и ширине потока, т.е. для условий плоской задачи, записывается в виде:
 (11)
(11)
Значения ∆х и ∆z связаны зависимостью:
 (12)
(12)
Таблица 1
Сетка для расчета турбулентной диффузии в условиях плоской задачи (вид на водоток сверху)
 Номер элемента Номер элемента
|  k k
| k+1 | k+2 |
| экстраполяционный | Ck1 экстр | ||
| Боковая стенка 1 | Сkp1 | Ck+1,1 | |
| Ck2 | |||
| m-2 | Ck,m-2 | ||
| m-1 | Ck,m-1 | ||
| m | Ck,m | Ck+1,m | |
| m+1 | Ck,m+1 | ||
| m+2 | Ck,m+2 |  ∆x ∆x
|  ∆z ∆z
|
x
z
Коэффициент турбулентной диффузии определяется по формуле (4).
Когда загрязняющее вещество достигает граничных поверхностей потока, для расчета диффузии необходимо учитывать особые условия у стенок, уравнение (10), которое в конечных разностях запишется в виде:
 (13)
(13)
Поле концентраций и расчетную сетку можно условно распространить и за пределы потока (за сетку), т.е. проэкстраполировать на концентрацию за ограничивающую водный поток поверхность.
При этом экстраполяционное значение концентрации Сk экстр в элементе, примыкающем к внешней поверхности стенки, и значение концентрации Сk,1 в элементе, находящемся в потоке и примыкающем к внутренней поверхности стенки, должны удовлетворять условию (14), что возможно
Сk экстр= Сk,1. (14)
Соотношение (15) определяет правило экстраполяции концентрации загрязняющего вещества. При определении диффузии экстраполяционные значения концентрации используют как действительные. При выполнении расчета на плане водного объекта обозначают место поступления сточных вод в водный объект (начальный створ). Ниже по течению поток схематизируется и делится на расчетные элементы. Скорость поступления сточных вод в водный объект в месте сброса Vст принимается равной скорости течения водотока Vср.
Вычисляется условная площадь поперечного сечения потока δ в месте его впадения при расходе сточных вод qст по формуле:
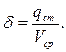 (15)
(15)
Определение ширины загрязненной струи потока b в нулевом створе производится по формуле:
 (16)
(16)
В соответствии с величиной b назначается ширина расчетного элемента ∆z.
Наиболее допустимая величина ∆z при береговом сбросе сточных вод находится из соотношения:
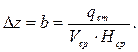 (17)
(17)
При выпуске сточных вод на некотором расстоянии от берега или в фарватере величина ∆z находится из соотношения:
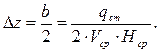 (18)
(18)
Необходимо соблюдать условие, при котором при назначении величины ∆z выполняется неравенство:
 (19)
(19)
где В – ширина потока.
Таким образом, при расчете турбулентной диффузии весь участок потока (от нулевого створа до расчетного или створа, который нас интересует по условию решаемой задачи) делят на клетки со сторонами ∆z и ∆х, получая расчетную сетку.
Клетки, попавшие в водоток со сточными водами в начальном поперечнике (нулевой створ), заполняются числами, выражающими концентрацию загрязняющего вещества в сточной воде, остальные клетки заполняют числами, отражающими естественную концентрацию загрязняющего вещества в водотоке (в частном случае это может быть нулевая концентрация).






