Модели случайных сигналов и помех [2, 28]

Наиболее распространенными моделями случайных сигналов и помех являются телеграфный сигнал, белый шум, гауссовский случайный процесс, гауссовский шум.

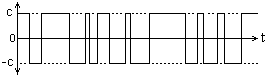Рис. 17.4.1. Телеграфный сигнал.

Телеграфный сигнал - это случайный процесс x_k(t), представляющий собой последовательность прямоугольных положительных и отрицательных импульсов со случайными длительностями и детерминированными значениями амплитуд c и -с, причем перемены знака внутри любого интервала (t, t+t) происходят с интенсивностью a в случайные моменты времени и не зависят от процессов в смежных временных интервалах. Если считать случайной величиной телеграфного сигнала значение n - количество перемен знака внутри интервала t, то распределение вероятностей значений n будет описываться законом Пуассона:

P(n) = (a|t|)² exp(-a|t|)/n! (17.4.1)

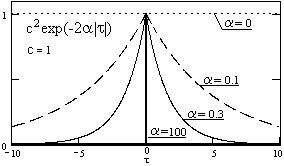Рис. 17.4.2. Функция корреляции сигнала.

При вычислении корреляционной функции телеграфного сигнала каждое отдельное произведение x_k(t)x_k(t+t) равно либо с², либо -с² в зависимости от совпадения или несовпадения знаков x_k(t) и x_k(t+t), причем вероятность с² равна сумме вероятностей Р(0)+Р(2)+Р(4)+..., а вероятность -с² определяется соответственно суммой вероятностей Р(1)+Р(3)+Р(5)+....

Следовательно:

R_x(t) = M{x_k(t)x_k(t+t)}= c² (-1)ⁿP(n) =

= c² exp(-a|t|) (-1)ⁿ(a|t)ⁿ/n! = c² exp(-2a|t|). (17.4.2)

Параметр a полностью определяет ковариационные и спектральные свойства телеграфного сигнала. При a Þ 0 характеристики сигнала приближаются к характеристикам постоянной составляющей, при a Þ ¥ - к характеристикам белого шума.

Интервал ковариации сигнала:

T_k = 2 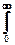(R_x(t)/c²) dt = 2/a. (17.4.3)

Отсюда следует, что чем больше a, тем меньше время ковариации процесса. При a Þ 0 T_k Þ ¥ и процесс вырождается в детерминированный (стремится к постоянной составляющей). При a Þ ¥ T_k Þ 0 и процесс вырождается в белый шум с некоррелированными отсчетами даже на соседних временных точках.

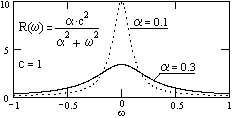Рис. 17.4.3. Спектр сигнала.

Двусторонняя спектральная плотность сигнала:

S_x(w) = 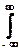R_x(t) exp(-jwt) dt = ac²/(a²+w²). (17.4.4)

Односторонняя спектральная плотность:

G_x(w)=2 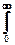R_x(t) exp(-jwt) dt= 2ac²/(a²+w²). (17.4.5)

Ширина спектра телеграфного сигнала:

B_k = 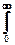G_x(w) dw/G_x(0) º 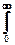S_x(w) dw/S_x(0) = ap. (17.4.6)

Отсюда следует, что спектр случайного процесса тем шире, чем меньше интервал ковариации процесса.

Белый шум является стационарным случайным процессом x(t) с постоянной спектральной плотностью G_x(f) = s², равной дисперсии значений x(t). Другими словами, все спектральные составляющие белого шума имеют одинаковую энергию (как белый цвет содержит все цвета видимого спектра).

По своему физическому смыслу спектральная плотность - это мощность процесса, которая приходится на 1 Гц полосы частот. Но тогда идеального белого шума на практике не может существовать, так как для него должно было бы выполняться условие:

R_x(0) = 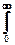G_x(f) df = (s²/2)×d(0) = ¥, (17.4.7)

т.е. мощность белого шума и его дисперсия равны бесконечности, а значения шума не коррелированны для любых |t| ¹ 0, так как корреляционная функция представляет собой идеальный дельта-импульс. Тем не менее многие помехи в радиотехнике, в технике связи и в других отраслях рассматривают как белый шум, если выполняется следующее соотношение между шириной спектров полезных сигналов и шумов

B_{k.сигнал}/B_k.шум << 1,

и спектральная плотность шумов слабо изменяется в интервале спектра сигнала.

Рис. 17.4.4. Функции корреляции белого шума в частотном интервале 0-В.

Если частотный диапазон спектра, на котором рассматриваются сигналы и помехи, равен 0-В, то спектральная плотность шума задается в виде:

G_x(f) = s², 0 £ f £ B; G_x(f) = 0, f > B, (17.4.8)

при этом корреляционная функция шума определяется выражением:

R_x(t) = s²B×sin(2pBt) / 2pBt. (17.4.9)

Эффективная шумовая ширина спектра:

B_k = R_x(0)/G_x(f)_max = B. (17.4.10)

Эффективное шумовое время ковариации:

T_k = 2 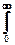|R_x(t)|dt /R_x(0). (17.4.11)

Реальное шумовое время ковариации целесообразно определить по ширине главного максимума функции R_x(t), в котором сосредоточена основная часть энергии шумов, при этом T_k = 1/В и B_kT_k = 1, т.е. соотношение неопределенности выполняется.

Как следует из всех этих выражений и наглядно видно на рис. 17.4.4, при ограничении частотного диапазона в шумах появляется определенная ковариация между значениями и чем меньше частотный диапазон шумов, тем больше их радиус ковариации. По существу, ограничение частотного диапазона шумов определенным диапазоном эквивалентно фильтрации белого шума частотным фильтром с соответствующей шириной полосы пропускания, при этом, в полном соответствии с выражением (17.3.7), корреляционная функция импульсного отклика фильтра переносится на шум.

Гауссовский шум возникает при суммировании статистически независимых белых шумов и имеет следующую функцию корреляции:

R_x(t) = a exp(-2ps²t²). (17.4.12)

Спектральная плотность шумов:

S_x(f) = (a/s 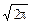) exp(-f²/2s²), - ¥ < f < ¥. (17.4.13)

Эффективные шумовые ширина спектра и время ковариации:

B_k = s 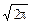/2 = 1.25s, T_k = 1/s 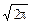= 0.4/s. (17.4.14)

Соотношение неопределенности превращается в равенство: B_kT_k = 1/2.

Гауссовские случайные процессы преобладают в практических задачах. Случайный процесс x(t) называется гауссовским, если для любого набора фиксированных моментов времени t_n случайные величины x(t_n) подчиняются многомерному нормальному распределению. Плотность вероятностей мгновенных значений x(t) эргодического гауссовского процесса определяется выражением:

p(x) = (s_x 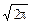)^-1 exp(-(x-m_x)²/2s²). (17.4.15)

Среднее значение и его оценка по достаточно большому интервалу Т:

m_x = 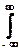xp(x) dx, m_x » (1/T) 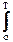x(t) dt.

При нулевом среднем (или при центрировании функции x(t) для упрощения расчетов) дисперсия не зависит от t и равна:

s_x² = 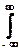x² p(x) dx.

Оценка дисперсии при больших Т:

s_x²» (1/T) 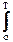x²(t) dt = 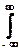S_x(f) df = 2 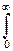S_x(f) df = 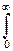G_x(f) df. (17.4.16)

Следовательно, плотность вероятностей гауссовского процесса полностью характеризуется спектральной плотностью, по которой можно определить значение дисперсии процесса. На вид спектральных плотностей и соответствующих им ковариационных функций никаких ограничений не накладывается.

 

литература

1. Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Высшая школа, 1988.- 448 с.

2. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.

25. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 608 с.

26. Вероятностные методы в вычислительной технике: Учебное пособие для вузов./ А.В.Крайников и др. - М.: Высшая школа, 1986. - 312 с.

26. Вероятностные методы в вычислительной технике: Учебное пособие для вузов./ А.В.Крайников и др. - М.: Высшая школа, 1986. - 312 с.

27. Гурский Е.И. Теория вероятностей с элементами математической статистики: Учебное пособие для вузов. - М.: Высшая школа, 1971.- 328 с.

28. Игнатов В.А. Теория информации и передачи сигналов. - М.: Советское радио, 1979.