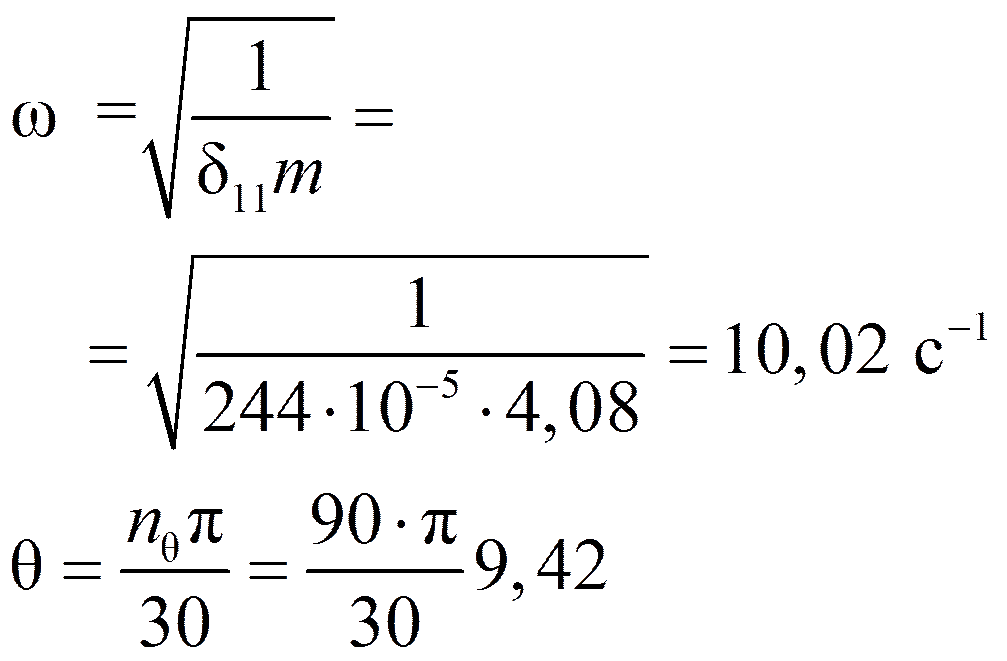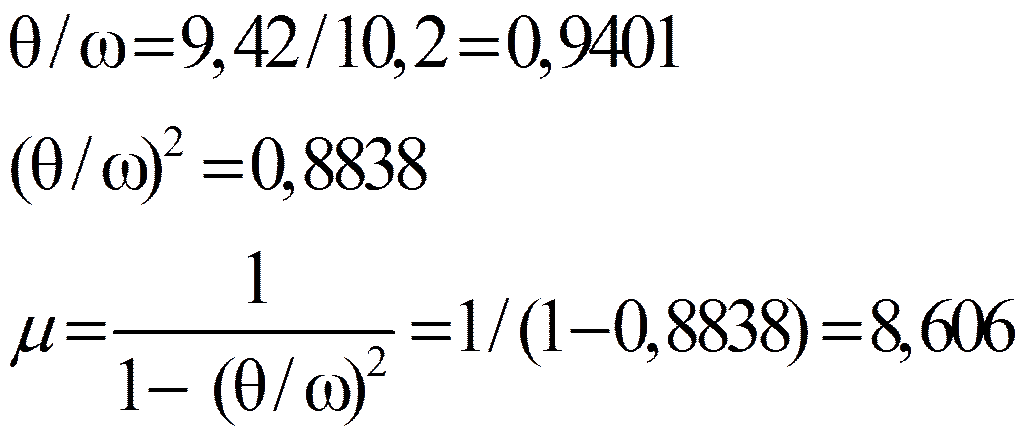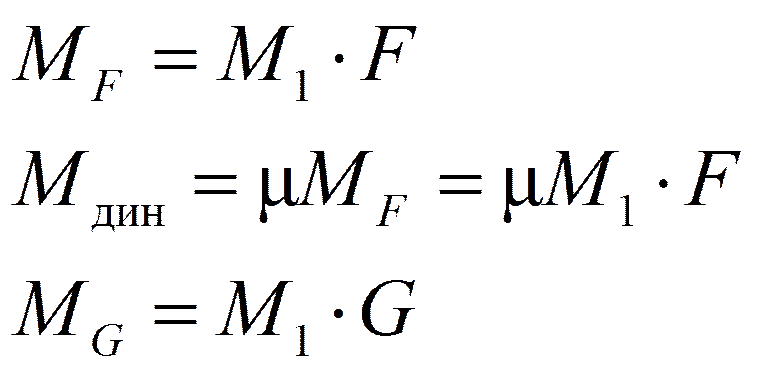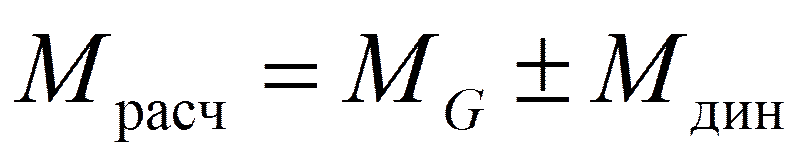Динамика
Введение
В.1. Виды динамических нагрузок
· вибрационная;
· ударная;
· подвижная;
· кратковременная (импульс);
· сейсмическая.
В.2. Виды колебаний
· свободные;
· вынужденные.
В.3. Степени свободы масс
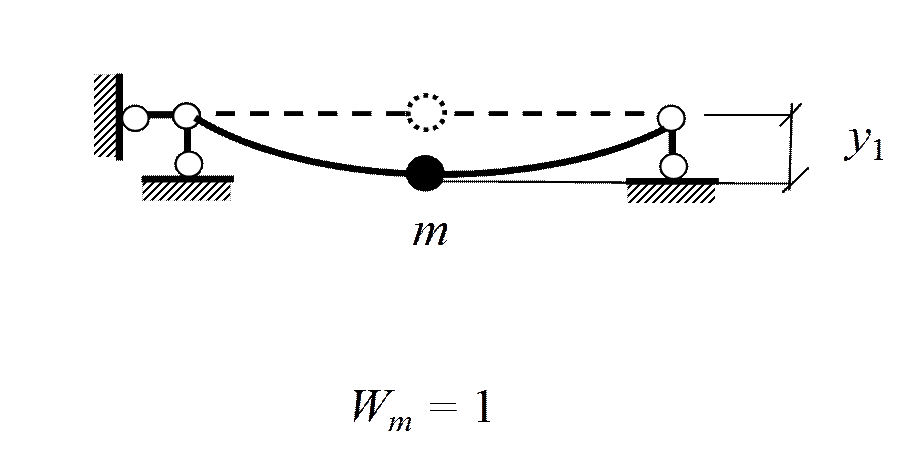
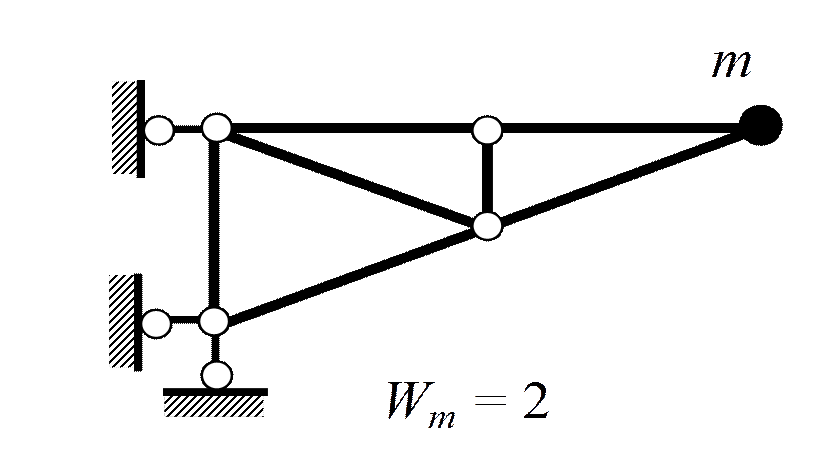
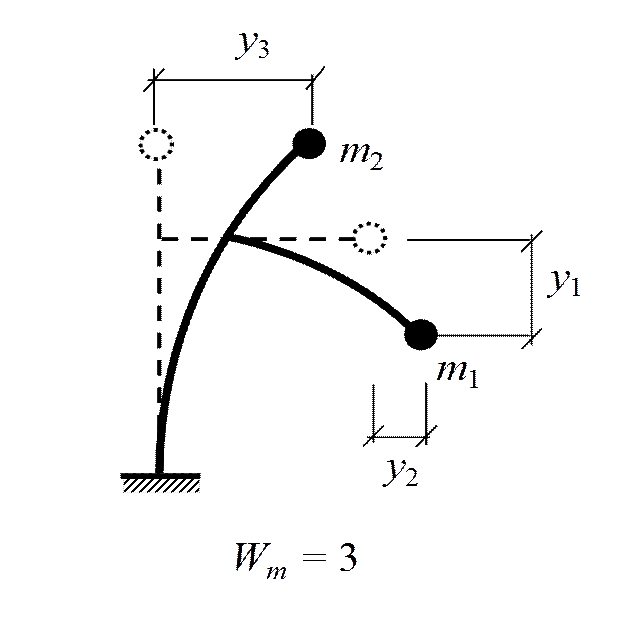

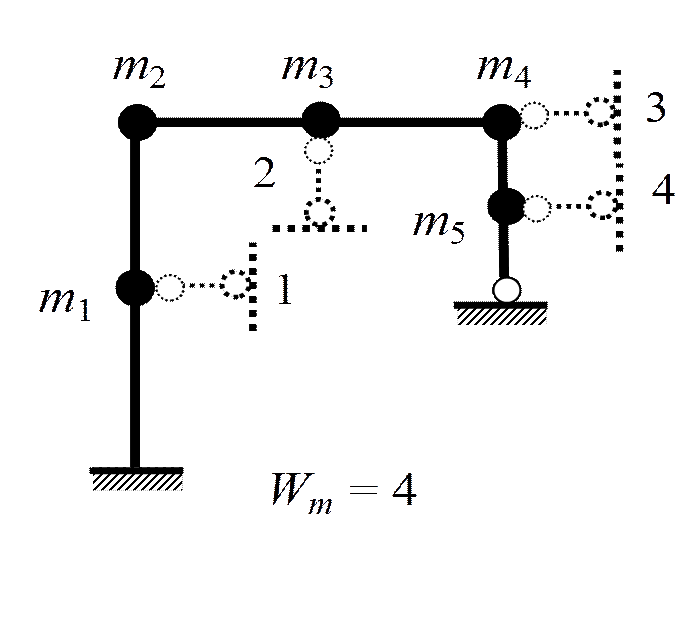
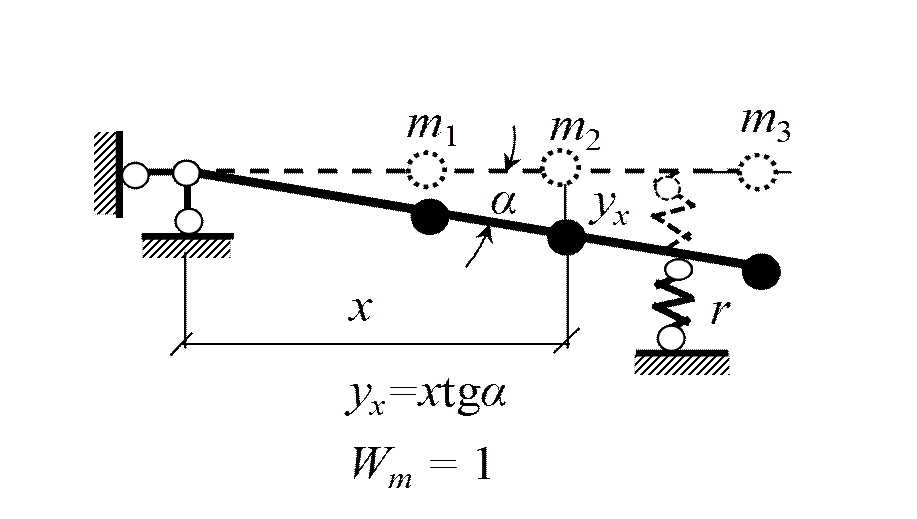


1. Колебания упругих систем с одной степенью свободы
1.1.Свободные
колебания

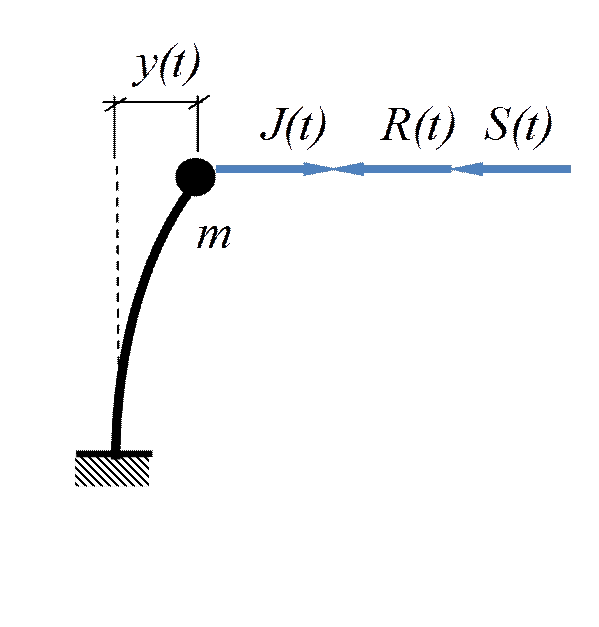


R(t) + S(t) – J(t) = 0
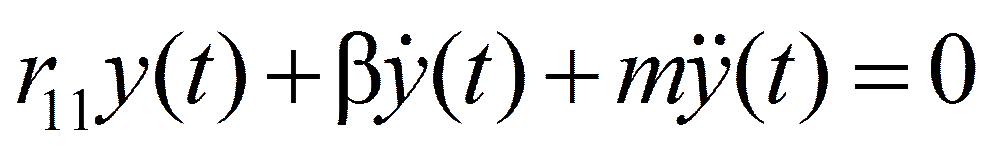
2 k =β/ m; ω2 = r11/ m
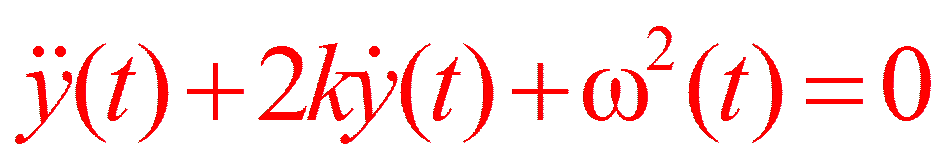
.
Свободные незатухающие колебания
S(t)= 0
2 k= 0


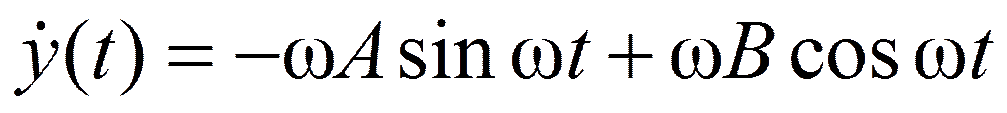
При
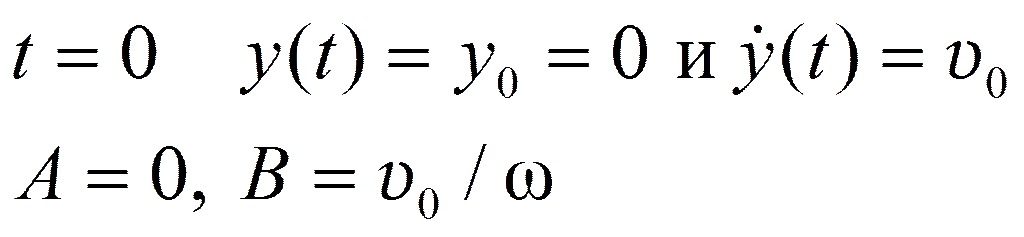
 .
.
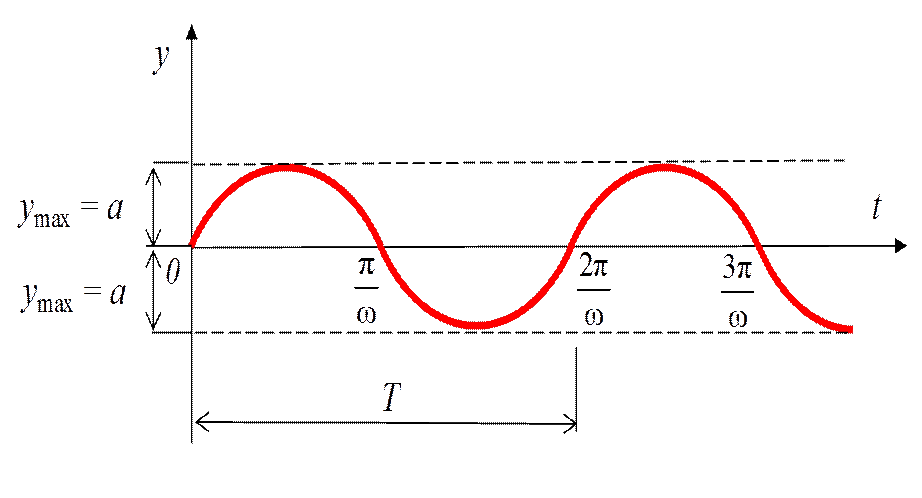
a 2 a
T = 2π/ω
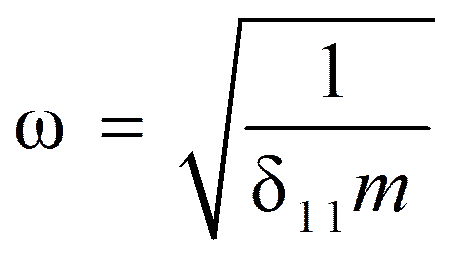
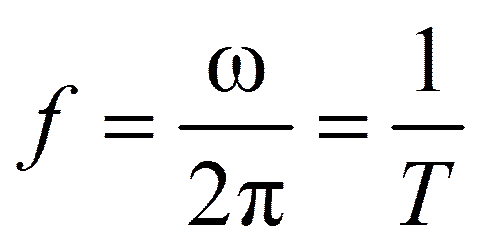
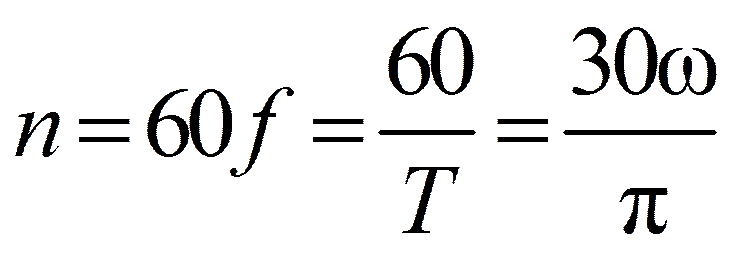 .
.
Свободные затухающие колебания
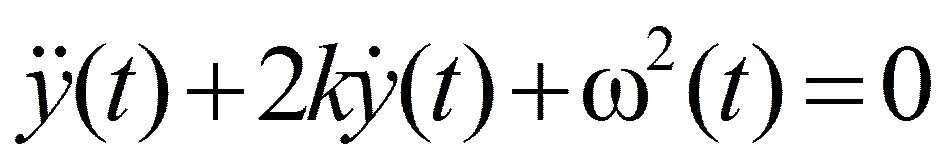
При
 ,
,
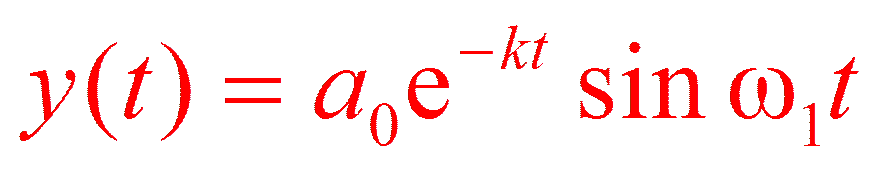

a 0= v 0/ω1
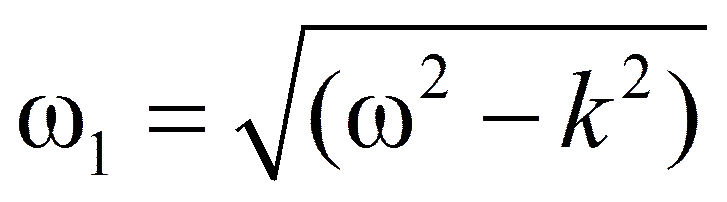

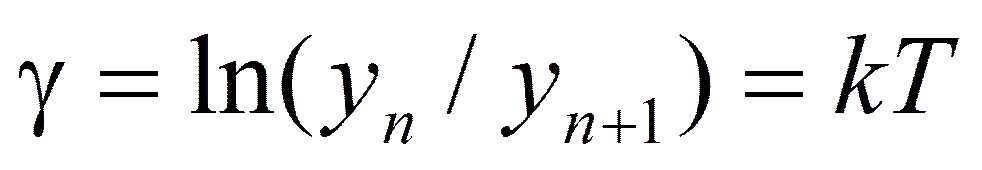
Значения коэффициентов поглощения ψ = 2 kT
| Амплитуда инерционной силы, кН | Железобетон | Кирпичная кладка | Дерево | Сталь прокатная |
| < 1 | 0,314 | 0,251 | 0,188 | 0,063 |
| ≥ 1 | 0,628 | 0,503 | 0,314 | 0,157 |
При ω1 ≈ ω
T = 2π/ω1
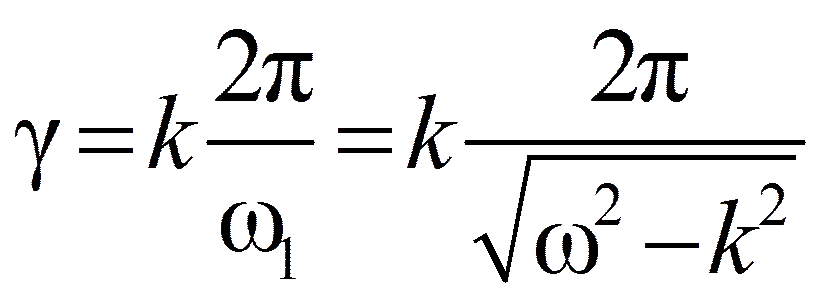
. 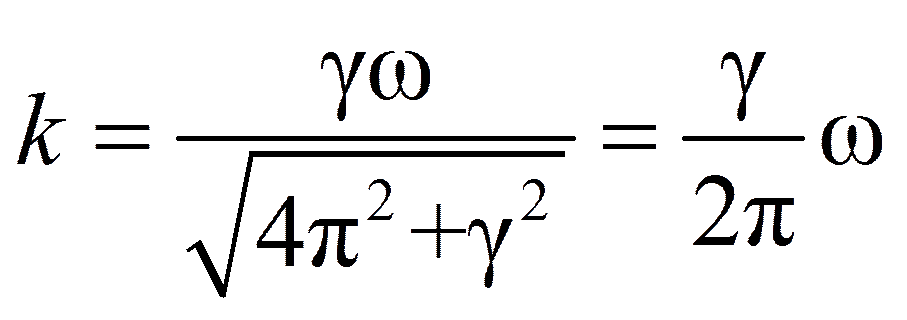
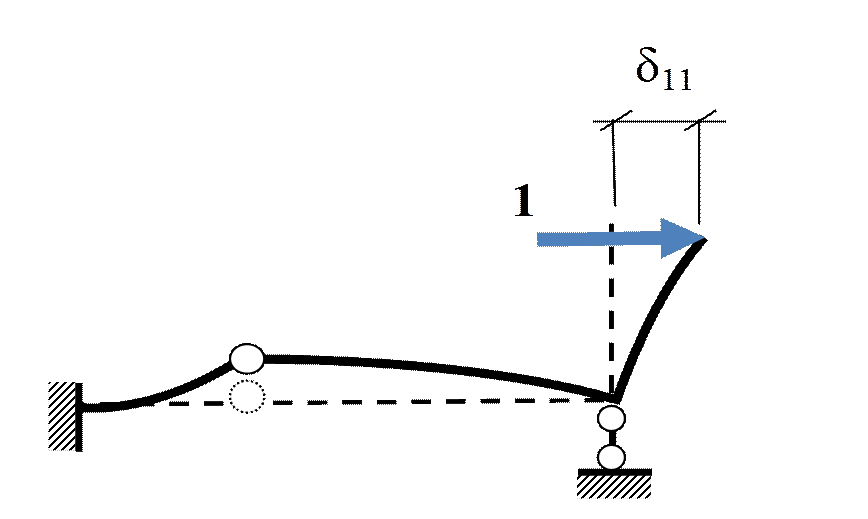
Пример 1. Определить ω, T, n, f
при EI = 3150 кН·м2, m =0,25 т.

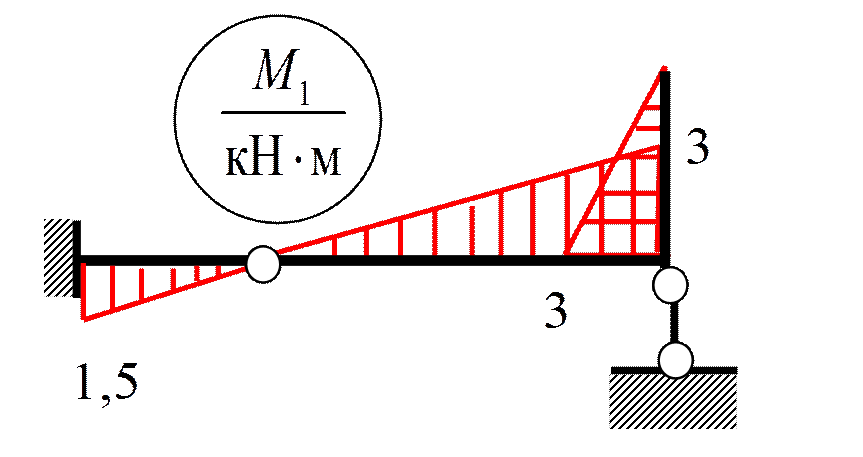



Пример 2. Определить ω и T,
при EI = 16200 кН·м2, m =3 т.
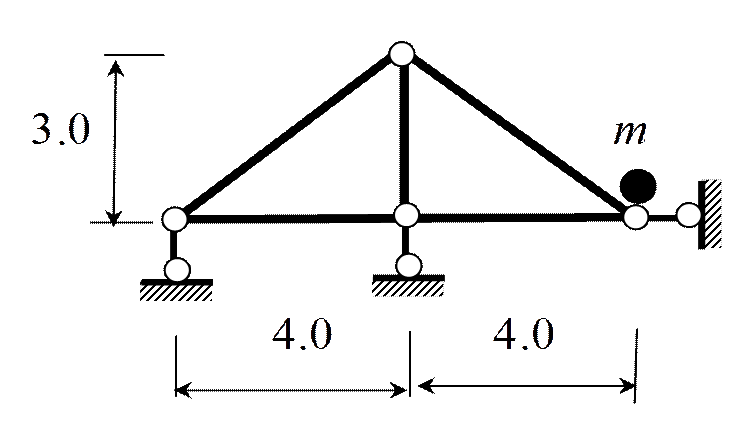
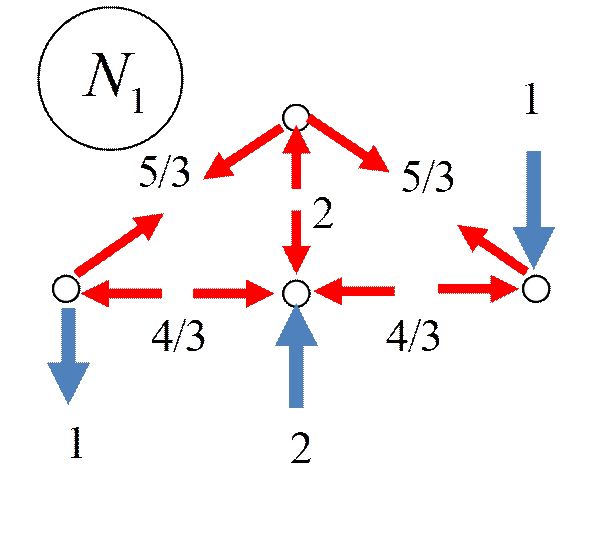
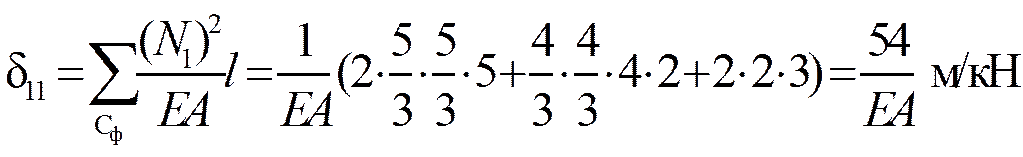

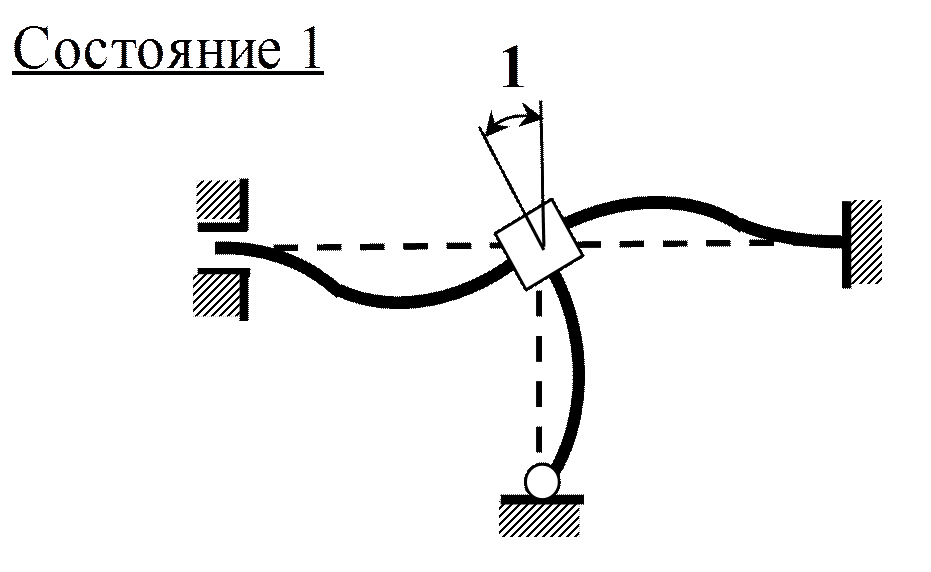
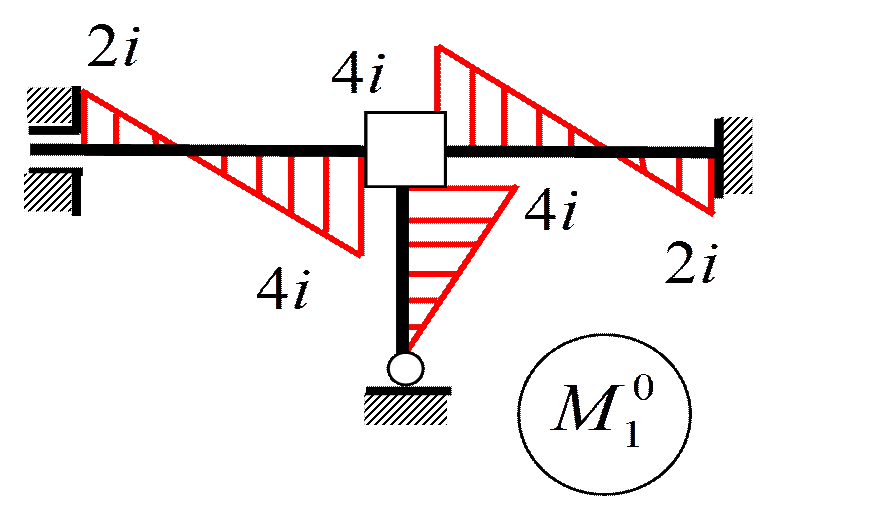
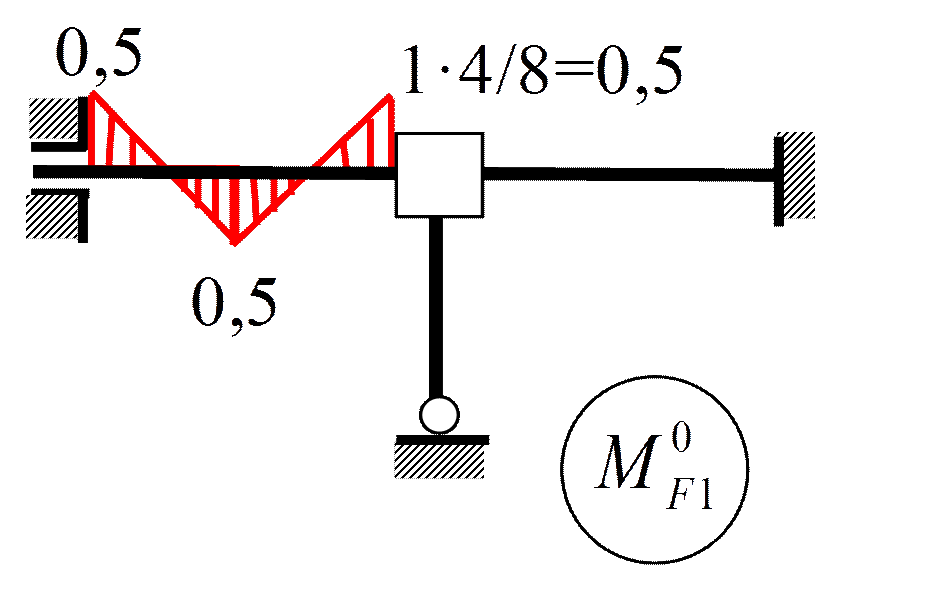
Пример 3. Определить ω
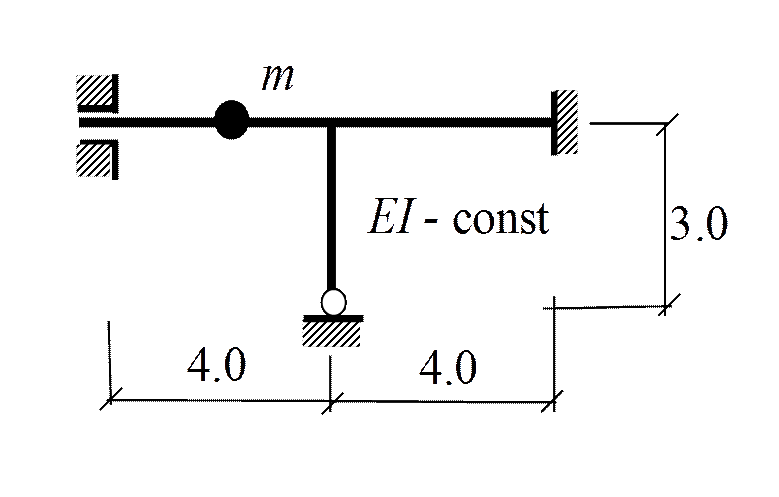

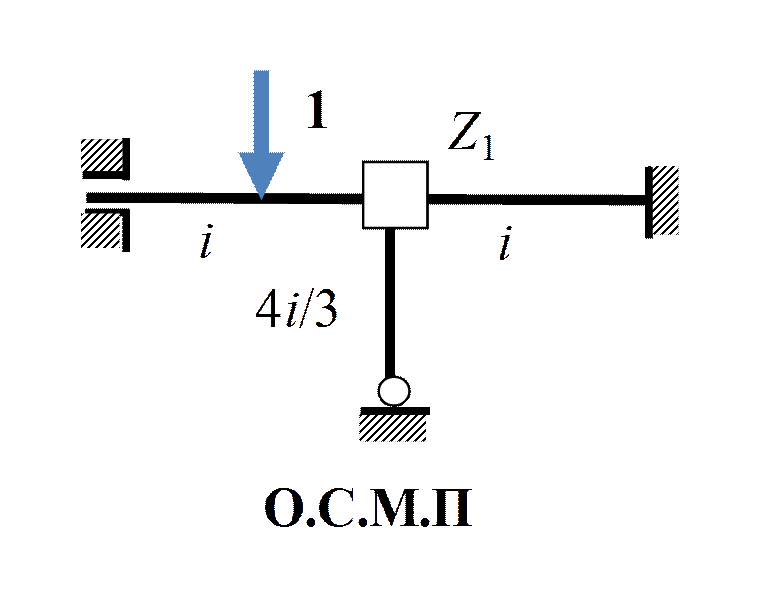
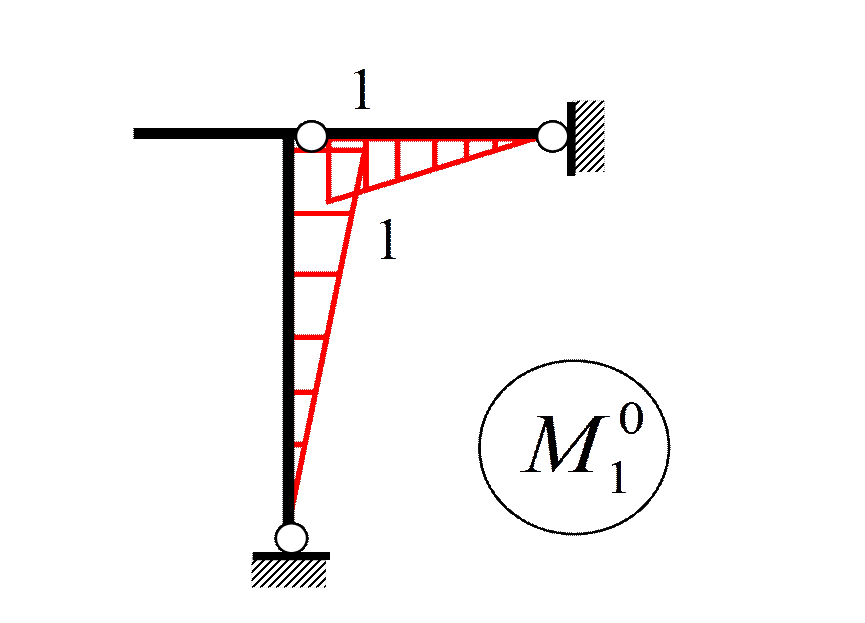
r 11 Z 1+ r 1 F =0
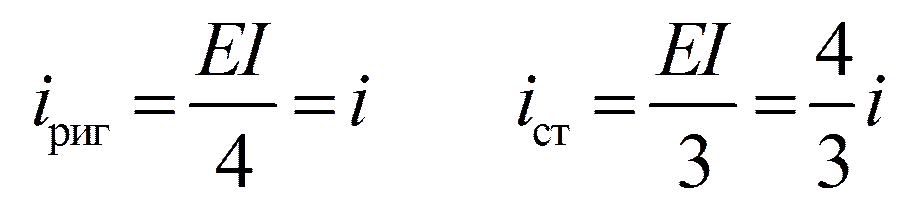
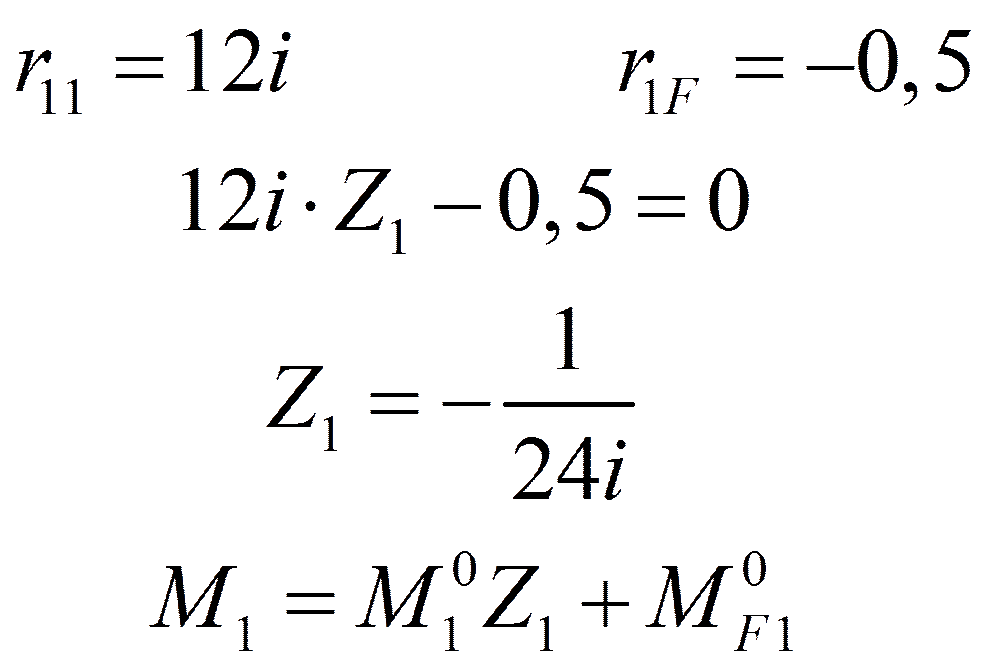
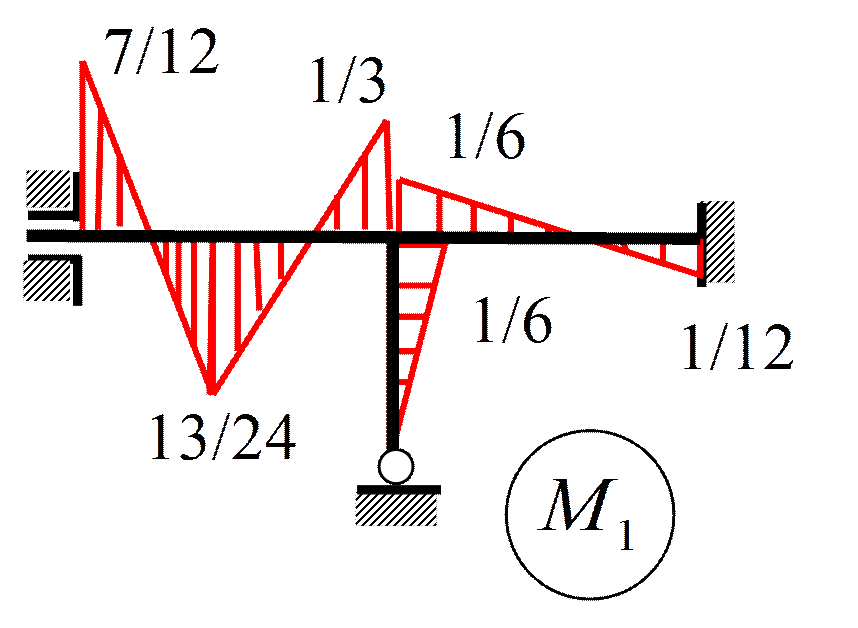
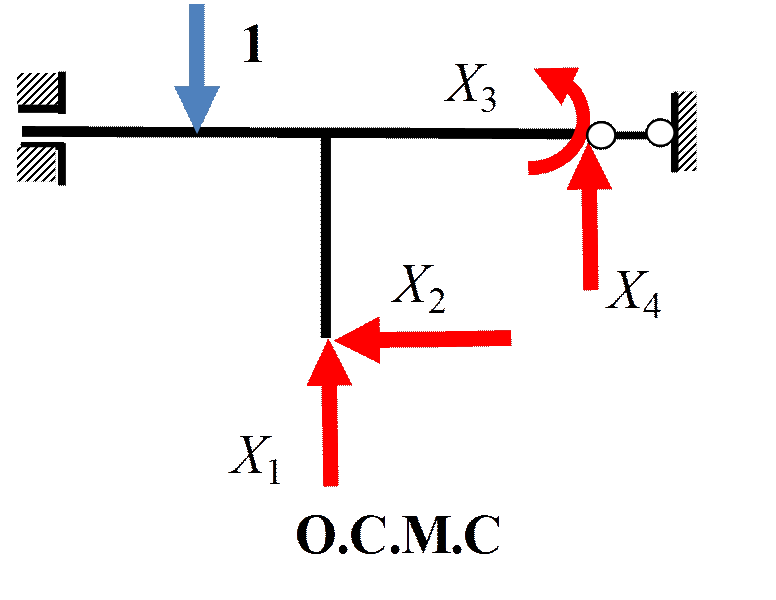

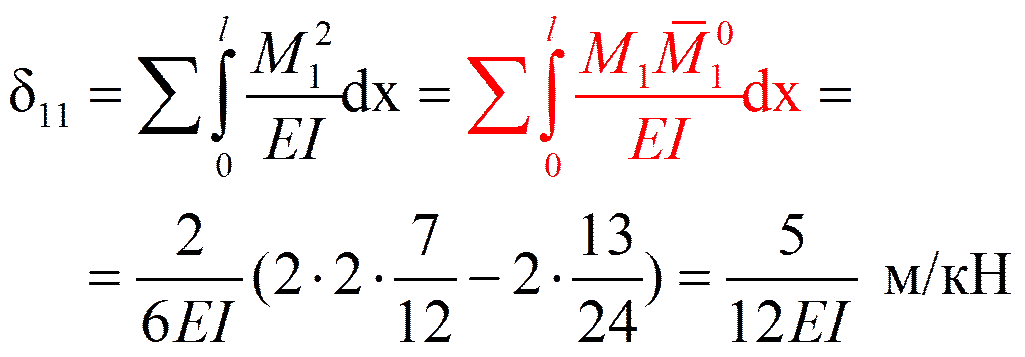

1.2.Вынужденные колебания
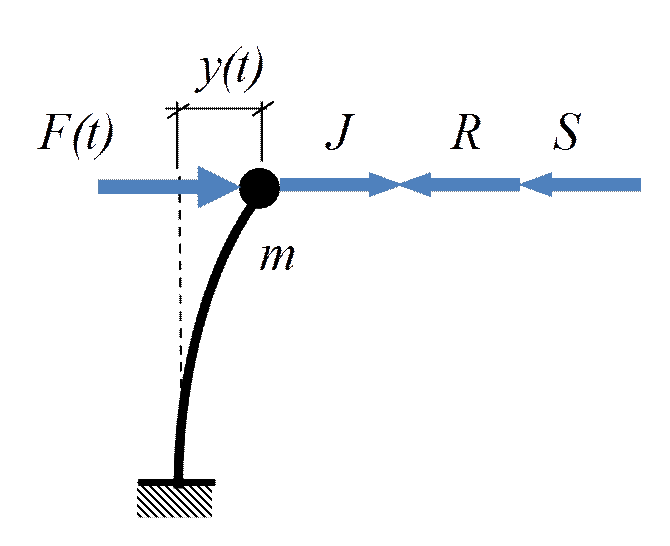
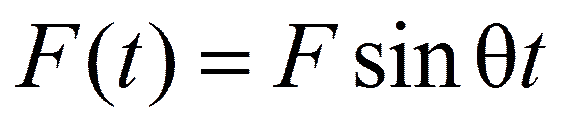
R + S − J −F sinθ t= 0
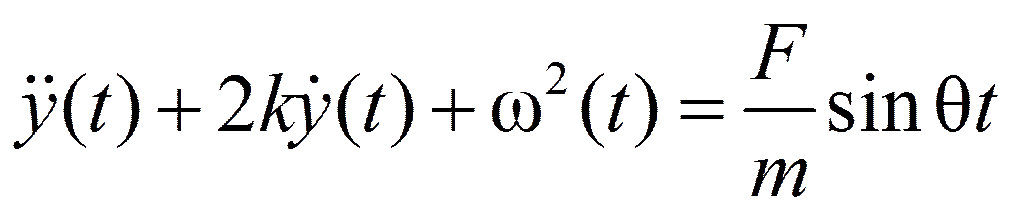 .
.
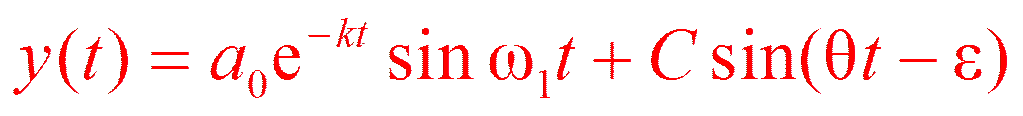
При t = 0

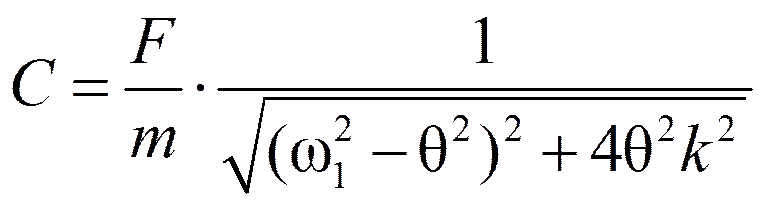
Или, т.к.


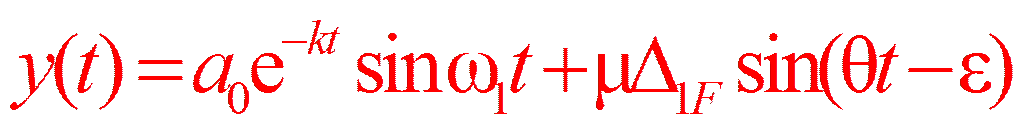

y дин = μ Δ1F.
M дин = μ MF;
Q дин = μ QF;
N дин = μ NF;
σ дин = μ σF и т.д.
ω1 ≈ ω
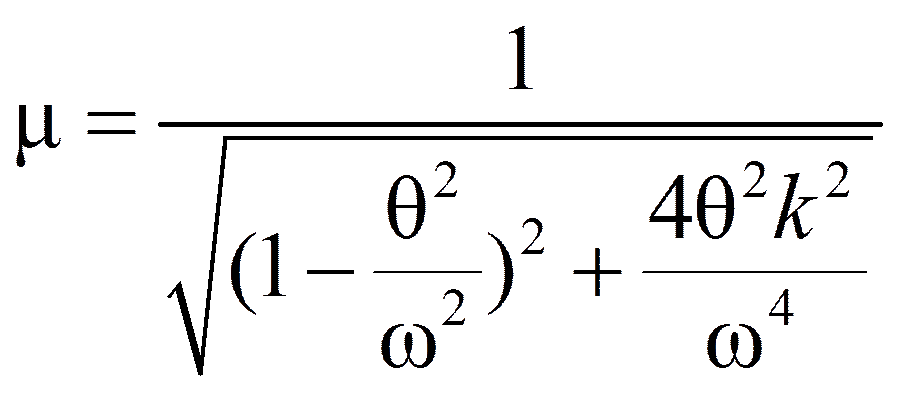
либо
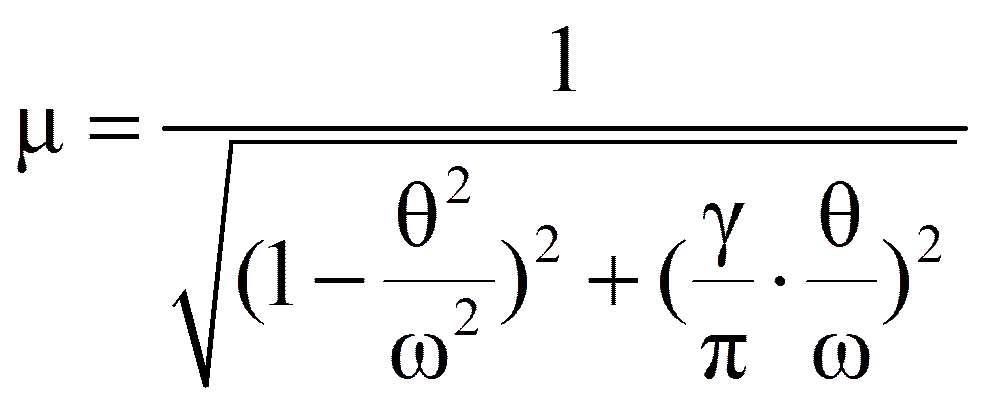

при θ= ω
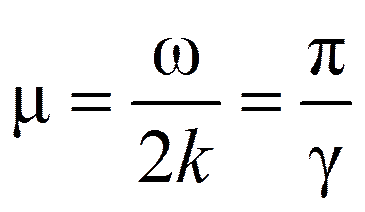 .
.
при (θ/ω)2 = 1 – γ2/2π2
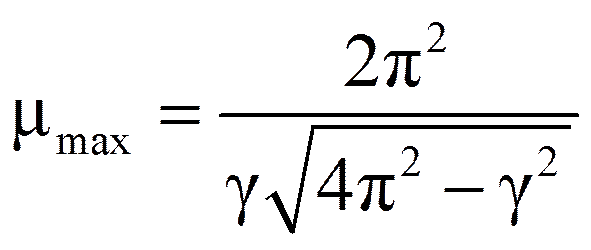
при k= 0
 .
.

Пример 4.
Проверить прочность наиболее опасного сечения и определить максимальный прогиб в балке при работе двигателя массой m = 3,5 т. Число оборотов n = 500 об / мин.
Масса неуравновешенных частей двигателя m 1 = 0,146 т, их эксцентриситет относительно оси вращения e = 0,0228 м.
Балка: сталь С245 (Ry = 245 МПа),
сечение – дв. № 30
(Iz = 7080 см4, Wz = 472 см3)
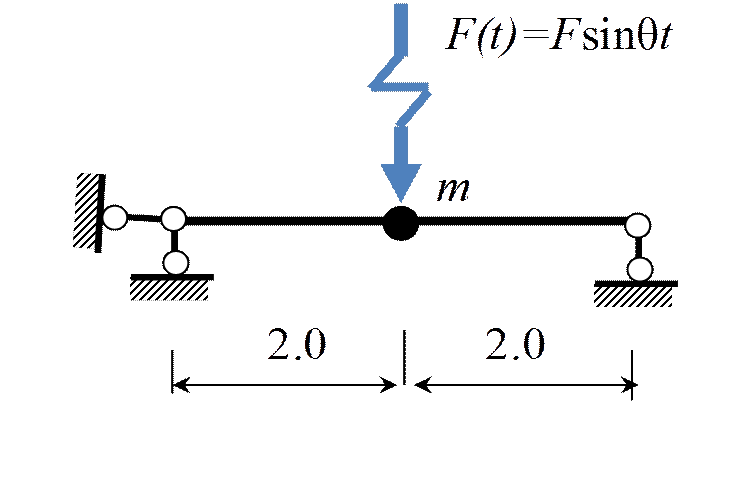
EI = 2,06·108·7080·10-8 = 14585 кН·м2



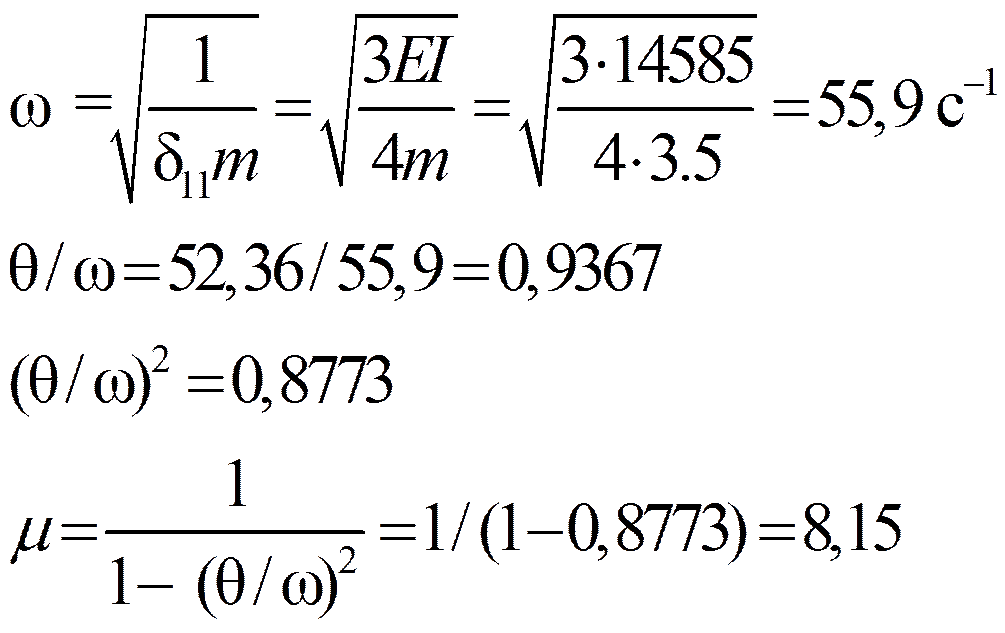

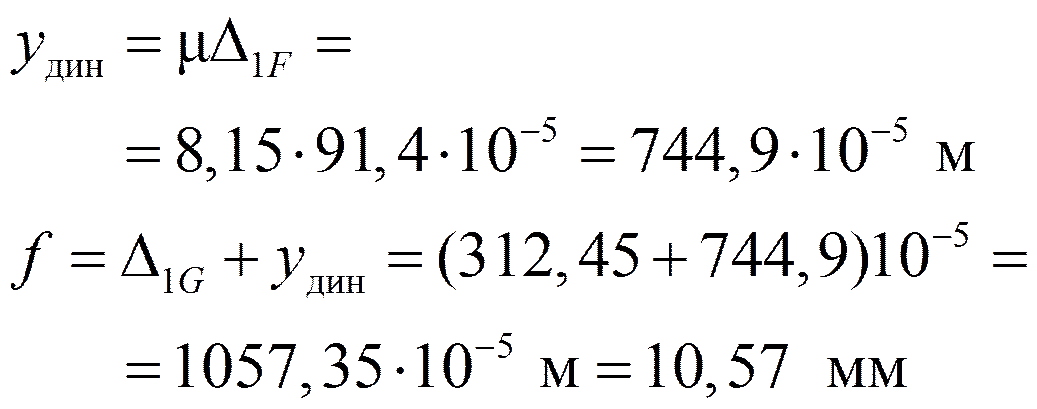
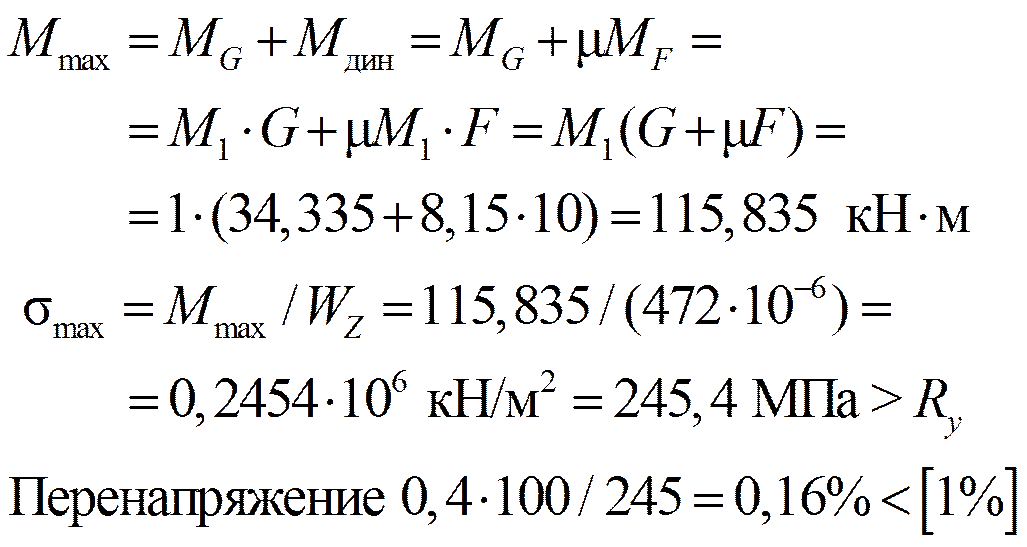
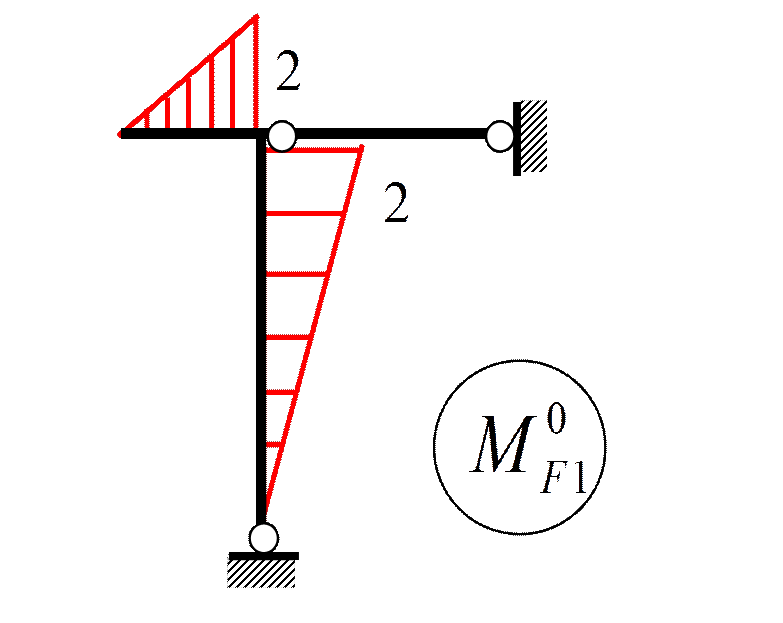
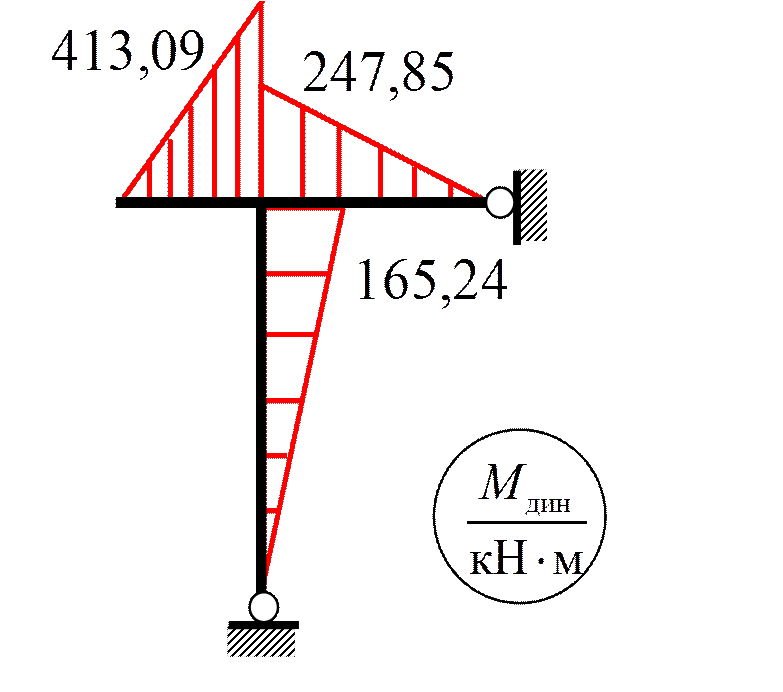
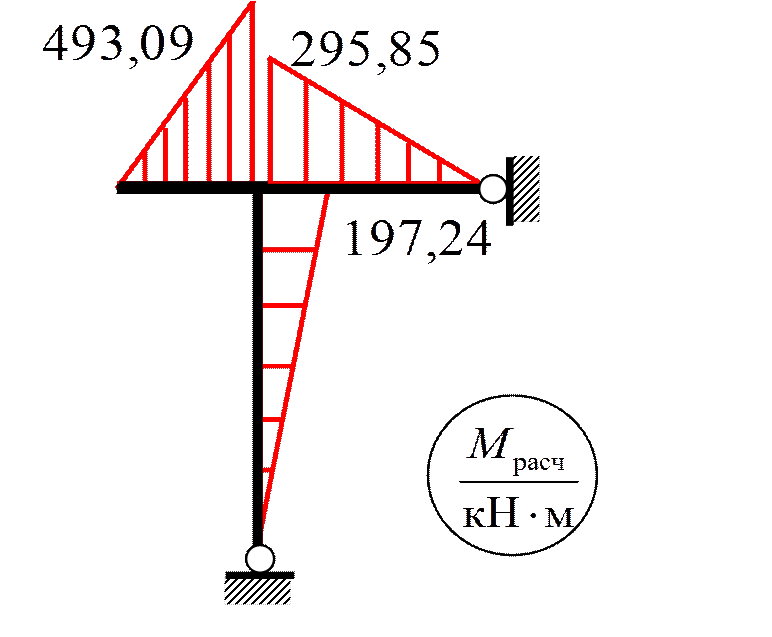
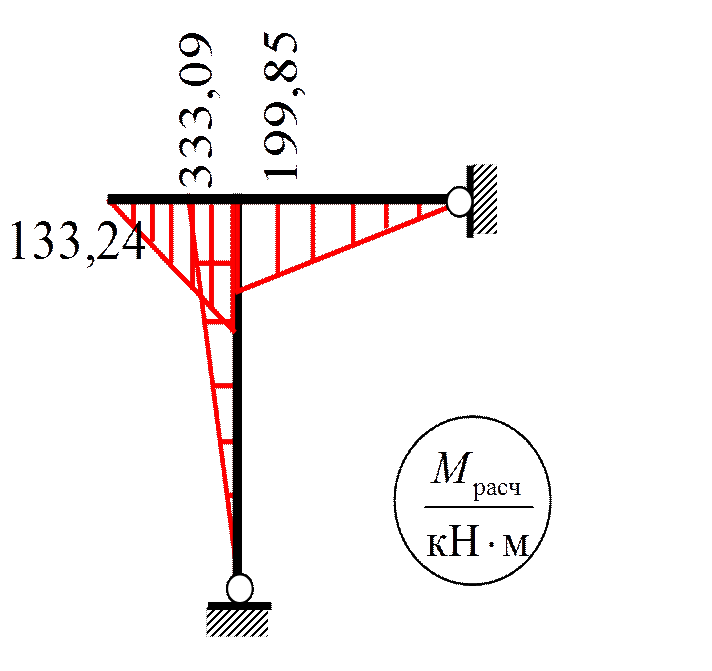
Пример 5. Построить M дин и M расч при следующих данных:
G = 40 кН;
F (t) = 24sinθ t кН;
n θ = 90 об/мин;
EI = 2400 кН·м2