Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменения уровней ряда, а именно:
· метод укрупнения интервалов,
· метод скользящей средней
· аналитическое выравнивание.
Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выровненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов называются сглаживанием или выравниванием рядов динамики.
Метод укрупнения интервалов
Простейший метод сглаживания уровней ряда — укрупнение интервалов, для которых определяется итоговое значение или средняя величина исследуемого показателя. Этот метод особенно эффективен, если первоначальные уровни ряда относятся к коротким промежуткам времени. Например, если имеются ежесуточные данные за месяц, то в таком ряду возможны значительные колебания уровней, так как чем меньше период, за который приводятся данные, тем больше влияние случайных факторов.
Чтобы устранить это влияние, рекомендуется укрупнить интервалы времени, например до 5 или 10 дней, и для этих укрупненных интервалов рассчитать общий или средний показатель. В ряду с укрупненными интервалами времени закономерность изменения уровней будет более наглядной. Неделя – месяц – квартал – полугодие – год.
Метод скользящей средней
Фактические уровни заменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих t уровней ряда.
Например, если принять t = 3, то сначала рассчитывается средняя величина из первых трех уровней, затем находится средняя величина из второго, третьего и четвертого уровней, потом из третьего, четвертого и пятого и т.д., т.е. каждый раз в сумме трех уровней появляется один новый уровень, а два остаются прежними. Это и обусловливает взаимопогашение случайных колебаний в средних уровнях. Рассчитанные из t членов скользящие средние относятся к середине (центру) каждого рассматриваемого интервала. Сглаживание методом скользящей средней можно проводить по любому числу членов t, но удобнее, если t — нечетное число, так как в этом случае скользящая средняя сразу относится к конкретной временной точке — середине (центру) интервала. Если же t — четное, то скользящая средняя относится к промежутку между временными точками: например, при сглаживании по четырем членам средняя из первых четырех уровней будет находиться между второй и третьей датой, следующая средняя — между третьей и четвертой и т.д. Тогда, чтобы сглаженные уровни относились непосредственно к конкретным временным точкам (датам), из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую и относят к определенной дате (периоду). Такой прием двойного расчета сглаженных уровней называется центрированием.
Недостатки метода скользящей средней
· сглаженный ряд «укорачивается» по сравнению с фактическим с двух концов: при нечетном t на (t — 1)/2 с каждого конца, а при четном — на t/2 с каждого конца.
· сглаживаются (устраняются) лишь случайные колебания.
· метод сглаживания – механический, эмпирический и не позволяет выразить общую тенденцию изменения уровней в виде математической модели.
Аналитическое выравнивание
Суть аналитического выравнивания заключается в замене эмпирических (фактических) уровней у теоретическими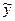 
, которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: 
=f(t).
В аналитическом выравнивании наиболее часто используются следующие простейшие функции:
- линейная
- гиперболическая
- параболическая
- показательная
- степенная
Выбор той или иной функции для выравнивания ряда динамики осуществляется на основании графического изображения эмпирических данных, дополняемого содержательным анализом особенностей развития исследуемого показателя (явления) и специфики разных функций, их возможности отразить те или иные нюансы развития. Определенную вспомогательную роль при выборе аналитической функции играют также механические приемы сглаживания (укрупнение интервалов и метод скользящей средней). Частично устраняя случайные колебания, они помогают более точно определить тренд и выбрать адекватную модель (уравнение) для аналитического выравнивания.
Параметры модели при аналитическом выравнивании определяют, решая систему нормальных уравнений, полученных методом наименьших квадратов. Но возможны и другие приемы.
Рассмотрим выравнивание по линейной функции . t – порядковый номер периодов или моментов времени. Коэффициенты модели определяют, решая систему нормальных уравнений:
Измерение колеблемости в рядах динамики
Колебания уровней ряда могут носить разный характер. Выделяют
· циклические (долгопериодические),
· сезонные (обнаруживаемые в рядах, где данные приведены за кварталы или месяцы)
Для измерения колеблемости уровней в рядах динамики могут использоваться показатели:
• размах (амплитуда), отклонений отдельных уровней от их средней (по модулю) или от тренда: 
• среднее линейное отклонение d (по модулю) отдельных уровней от общей средней или от тренда: 
• среднее квадратическое отклонение отдельных уровней от общей средней или от тренда: 
• относительный показатель колеблемости уровней: 
• относительный показатель линейной колеблемости уровней: 
Выявление и измерение сезонных колебаний
Сезонные колебания – периодически повторяющиеся из года в год повышение и снижение уровней в отдельные месяцы или кварталы.
Метод абсолютных (относительных) разностей
Определяют разность фактических уровней с выровненными уровнями. По полученным значениям или по их отношениям к выровненному уровню определяют наличие «сезонной волны».
