 .
.
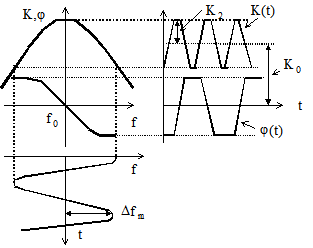
Рисунок 7.13 – АЧХ и ФЧХ селективного тракта приемника и временные зависимости
коэффициента передачи фазового сдвига, вносимого трактом
Из рисунка видно, что при изменении отклонения частоты по косинусоидальному закону из-за неидеальности АЧХ селективного тракта его коэффициент передачи изменяется во времени с удвоенной частотой модуляции
 .
.
В результате на выходе селективного тракта действует сигнал, модулированный не только по частоте, но и по амплитуде. Это приводит к нелинейным искажениям сигнала на выходе частотного детектора. Для их устранения необходимо использовать амплитудный ограничитель перед частотным детектором.
Из-за нелинейности ФЧХ вносимый селективным трактом фазовый сдвиг изменяется по закону, отличному от косинусоидального

Этот фазовый сдвиг приводит к приращению отклонения частоты ЧМ – сигнала, которое равно
 .
.
Таким образом, из-за нелинейности ФЧХ появляется третья гармоника отклонения частоты ЧМ - сигнала от среднего значения, что приводит к нелинейным искажениям сигнала на выходе частотного детектора.
7.2.2.Нелинейные искажения сигнала в частотном детекторе
Нелинейность детекторной характеристики (рисунок 7.14) является причиной возникновения нелинейных искажений выходного сигнала детектора.

|
Рисунок 7.14 – детекторная характеристика частотного детектора
В пределах раствора детекторной характеристики коэффициенты второй и третьей гармоник выходного сигнала детектора определяются следующими соотношениями
 , (7.5)
, (7.5)
где  - крутизна частотного детектора,
- крутизна частотного детектора,  и
и  -ее первая и вторая производные,
-ее первая и вторая производные,  - девиация частоты.
- девиация частоты.
Из приведенных соотношений видно, что с увеличением девиации частоты нелинейные искажения выходного сигнала увеличиваются.
7.3.Действие синусоидальной помехи на приемник частотной модуляции
На рисунке 7.15 показаны вектор немодулированного сигнала Uc, вектор помехи UП, вращающийся относительно вектора сигнала с частотой Ω = ωс – ωП, и вектор результиру- ющего колебания U. Вектор U качается относительно вектора Uc. Конец этого вектора перемещается по окружности. Фазовый сдвиг вектора результирующего колебания относительно вектора сигнала является функцией времени  . Максимальное по абсолютной величине значение этого фазового сдвига получается в точках A и B касания вектора
. Максимальное по абсолютной величине значение этого фазового сдвига получается в точках A и B касания вектора  окружности.
окружности.






