| Изохорный | Изобарный | Изотермический | Адиабатный (изотропный) (без теплообмена) | Политропный (теплоёмкость постоянна) | ||||||||||||||
1. V=const; V1 = V2; dV=0
  
3. Закон Шарля
4. ∆U = ∫CVdT = CV(T2-T1) = = U2-U1 - (по табл.)
∆h= ∫CPdT ≈ CP(T2-T1) = = h2-h1 - (табл.)
5. L расш. = PdV = 0. L полез.= ∫(-VdP) = V(P1-P2).
6. q =∆U=U2-U1= CV (T2-Т1) = = ∆h + V(P1-P2).
7. CV = f (T) - природа газа СV > 0 8. ∆SV = CV ln ∆S = S20 - S10 – R ln
| 1. P=const; α=1 / 273o
T=273+t°; V=V0(1+αt)
3. Закон Гей-Люсака
4. ∆U = ∫CVdT = CV(T2-T1)= = U2-U1 - (по табл.)
∆h = ∫CPdT ≈ CP(T2-T1)= = h2 - h1 - (по табл.)
5. L расшир.= ∫pdV = P(V2-V1)
L полез.= 0= -VdP. (Lтехн)
6. q=∆h=h2-h1=P(V2-V1)+∆U
7. Уравнение Майера: СP = CV + R 8. ∆SP = CP ln
∆S = S20 - S10
| 1. T=const; PV=const
Т1 = Т2; dТ = 0
2.
 
3. З-н Бойля-Мариотти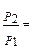  
4. ∆U = 0 = CV∆T ∆h = 0 = CP∆T 5. L расшир .= ∫PdV= ∫RT = RT ln L полез.=∫-VdP=∫-RT =RT*ln 6. q = L расш= L полез (Lтехн)
7. CT = ± ∞= δq /dT (dT→0) 8. ∆ST = R ln
S20 = S10; ∆ST = δq / T | 1. q=0; dq=0; PVK=const;
2. k=CP/CV=f(T) k=const
 
 ; 
4. ∆U = ∫CVdT ≈ CV(T2-T1) = = U2-U1 - (по табл.) ∆h = ∫CPdT ≈ CP(T2-T1) = = h2 - h1 - (по табл.) 5. L расш =∫PdV= = L расш = - (∆U) = U1-U2. L полез=∫(-VdP) = =
6. q =0 7. СK=0
8. ∆S = S20 - S10 – R ln | 1. PVn =const; n=const
2. Cn= f (T); Cn=const; n=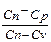 
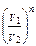3.  ;  =  4. ∆U = ∫CVdT ≈ CV (T2-T1) =
= U2-U1 - (по табл.)
∆h = ∫CPdT ≈ CP(T2-T1) =
= h2 - h1 - (по табл.)
5.Lрасш =  (P1V1-P2V2)=
=  P1V1  = 
(L техн) Lполез = nLрасш
6. q= ∆U+Lрасш = ∆h+Lполез
q=Cn (T2-T1); 7. Cn=CV 
8. ∆S = CV ln  + R ln  ;
. ∆S = CP ln - R ln  ;
.∆S = CP ln  + CV ln ;
∆S = S20 - S1 0 - R ln .
|
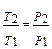
= CV ln 
1
2' q
q 
=
= L полез.
=
; L расш = L полез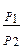
(P1V1- P2V2)= = 
P1V1 
= 
=
(P1V1-P2V2)=
L полез =(-∆h)=h1-h2; L полез= k L расш
= 0.