«Динамика конструкций и сооружений»
Цель задачи – нахождение собственных частот и форм колебаний при помощи решения проблемы собственных значений.
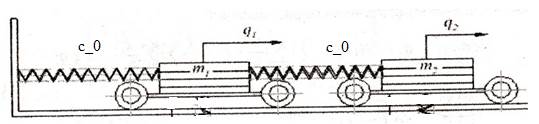
Рис.3.1. Система с двумя степенями свободы
Матрица жесткости системы на рис.3.1:
 (3)
(3)
Используя выражение (3), составим нижнюю треугольную матрицу:  (4)
(4)
Транспонируем ее и найдем произведение этих матриц:  (5)
(5)
Образуем систему уравнений, приравнивая элементы матриц [P] элементам МЖ [C]:
 (6)
(6)
Учтем свойство симметрии матрицы [H]  для этого подставим это равенство в систему уравнений:
для этого подставим это равенство в систему уравнений:
 (7)
(7)
Конвертируем этот список в матрицу и удаляем лишнее уравнение:
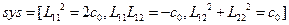 (8)
(8)
Конвертируем систему снова в список и сформируем список неизвестных:
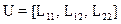 (9)
(9)
Решаем систему относительно неизвестных. С помощью функции allvalues находим эти решения в явном виде. Выделяем из этого списка списков список с положительными элементами на главной диагонали:
 (10)
(10)
Переформируем этот список в матрицу:  (11)
(11)
Транспонируем [L], обратим [L] и  . Сформируем матрицу масс, пренебрегая массами пружин:
. Сформируем матрицу масс, пренебрегая массами пружин:
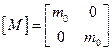 (12)
(12)
Первое умножение в формировании матрицы [H]:
 (13)
(13)
Второе умножение в формировании матрицы [H]:
 (14)
(14)
Найдем определитель матрицы [H]. Он равен сумме значений этой матрицы:
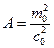 (15)
(15)
Составим единичную матрицу:
 (16)
(16)
Найдем определитель однородной системы. Он должен быть равен 0, т.к. другая возможность равенства нулю левой части - равенство нулю собственного вектора тривиальна, т.е. ничего не дает:
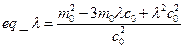 (17)
(17)
Решив Х.У., найдем собственные числа матрицы [H]:
 (18)
(18)
Выделяем первое собственное значение:  (19)
(19)
Выделяем второе собственное значение:  (20)
(20)
Произведение собственных чисел матрицы Р равно ее определителю:
 (21)
(21)
Сумма собственных чисел матрицы Р равна сумме ее диагональных членов:
 (22)
(22)
Находим первую собственную частоту: 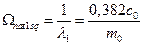 (23)
(23)
Находим вторую собственную частоту:  (24)
(24)
Теперь найдем их произведение, оно обратно к произведению собственных чисел:
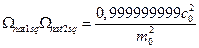 (25)
(25)
Сформируем вектор собственных чисел матрицы [H]:  (26)
(26)
Сформируем вектор собственных частот: 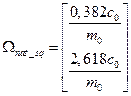 (27)
(27)
Найдём собственные формы системы с равными параметрами. Вектор х найдём, подставив:
 (28)
(28)
В первое уравнение, поэтому в квадратных скобках стоит [1]
 (29)
(29)
В этом первом уравнении произвольно положим 
Тогда 1-е уравнение примет вид:  (30)
(30)
Решив его, найдем вторую компоненту 1-го собственного вектора 
Сформируем 1-й собственный вектор, соответствующий первому собственному значению:
 (31)
(31)
Найдем 1-ю собственную форму колебаний:
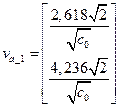 (32)
(32)
Так как она известна с точностью до произвольного множителя, то:
 (33)
(33)
Мы получили ту же форму, что и в теории колебаний. Теперь, чтобы найти второй вектор, соответствующий второму собственному числу, сформируем вначале этот вектор. Пока только обозначения
 (34)
(34)
Также произвольным положим  .
.
Так как работаем со вторым собственным числом, то надо взять второе уравнение и положили 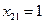 и
и  на
на 
 (35)
(35)
Найдем 
Сформируем второй собственный вектор: 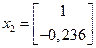 (36)
(36)
Найдем вторую собственную форму колебаний:
 (37)
(37)
Так как она известна с точностью до произвольного множителя, то она будет равна:
 (38)
(38)






