12.1. Основные положения и допущения для расчета мешающих влияний
Расчет напряжений мешающих влияний на линии связи, работающие на звуковых частотах, гораздо сложнее расчета напряжений опасных влияний. Основные трудности связаны с несинусоидальностью влияющего тока контактной сети и большой электрической длиной цепей. Для расчета напряжений мешающих влияний в основном используются похожие выражения, что и для расчета опасных влияний, усложненные указанными обстоятельствами. Основные положения расчета и некоторые отличия таковы.
1. В тяговой сети протекают несинусоидальные токи, приводящие к несинусоидальным наводимым напряжениям магнитного влияния. Расчеты наводимых напряжений в такой ситуации проводят, используя синусоидальные составляющие токов и напряжений, переходя к расчетам на гармониках. Основными источниками гармоник в тяговой сети являются выпрямители и инверторы тяговых подстанций при электрификации на постоянном токе, а на переменном токе - преобразователи электроподвижного состава.
2. На аппаратуру связи воздействует напряжение, которое, как правило, поступает с двух проводов. Поэтому далее чаще всего речь будет идти о двухпроводной цепи, в которой напряжение между проводами много меньше напряжения каждого провода относительно земли.
В двухпроводной линии оба провода оказываются под напряжениями U 1 и U 2 относительно земли, а на нагрузке линии напряжение равно U 12= U 1 - U 2. Напряжение это не равно нулю, во-первых, из-за разных расстояний от тяговой сети до каждого из проводов (поперечная асимметрия), во-вторых, из-за неодинаковости двух проводов по длине (продольная асимметрия). Ввиду малого расстояния между проводами, их скручивания или скрещивания преобладает обычно продольная асимметрия. Для расчета напряжения этой составляющей используют так называемый коэффициент чувствительности η = U 12/ U 0, где U 0≈ U 1≈ U 2. Таким образом, расчет напряжения мешающего влияния сводится к расчету напряжения на проводе относительно земли: U = ηU 0. Значения коэффициента чувствительности обычно определяют путем экспериментальных измерений.
3. Длина цепи, на которую рассчитывается влияние, велика в том смысле, что тяговая влияющая цепь составлена из нескольких межподстанционных зон. Напряжения от разных межподстанционных зон суммируются с использованием синусоидальных составляющих токов и напряжений. Длина цепи велика еще и в другом смысле: для высших гармоник нельзя считать цепь электрически короткой, поэтому необходимо пользоваться общими выражениями для процессов в цепях с распределенными параметрами.
4. Обычно напряжение электрического влияния оказывается много меньше, чем напряжение магнитного влияния, поскольку влияния обусловлены главным образом гармониками тока в тяговой сети, и далее рассмотрен расчет только напряжения магнитного влияния. При необходимости оба напряжения можно складывать по ранее приведенной методике.
12.2. Разложение периодических токов и напряжений в ряд Фурье
Расчет линейной цепи с несинусоидальными напряжениями и токами, в том числе и расчет влияний, в общем случае сводится к решению систем линейных дифференциальных уравнений, составленных на основании законов Кирхгофа или на основе производных из законов Кирхгофа методов. Но если разложить периодические токи и напряжения на сумму синусоидальных величин, то возможен расчет раздельно для каждой гармоники, то есть решение системы линейных алгебраических уравнений, с последующим сложением решений для гармоник. Такой подход проще, но требует предварительного разложения несинусоидальных источников на синусоидальные составляющие, то есть в ряд Фурье. Разложение в ряд Фурье базируется на теореме Фурье, которая формулируется следующим образом.
Всякая периодическая функция, удовлетворяющая условиям Дирихле, то есть имеющая за полный период конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в ряд Фурье:
Необходимо заметить, что в задачах электротехники все периодические токи и напряжения удовлетворяют условиям Дирихле (в которых разрывом первого рода называют скачок функции на конечную величину; тангенсоида, например, имеет разрывы второго рода). Поэтому можно сказать, что всякое периодическое напряжение или всякий периодический ток могут быть разложены в ряд Фурье.
В разложении в ряд Фурье A 0 - постоянная составляющая, A 1sin(ωt + φ 1) - основная волна или первая гармоника, которая имеет тот же период T =2 π / ω, что и исходная несинусоидальная функция; остальные слагаемые называют высшими гармониками. Частоты высших гармоник кратны основной частоте, определяемой периодом исходной функции.
Отдельное слагаемое ряда Фурье можно представить и в несколько ином виде:
,
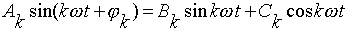где 
Коэффициенты ряда Фурье вычисляются из исходной функции следующим образом:
(28)
Довольно часто встречается ситуация, когда токи и напряжения удовлетворяют условию 
то есть кривая симметрична относительно оси абсцисс (рис. 33). Для такой кривой в разложении Фурье отсутствуют четные гармоники и постоянная составляющая:
(29)
Рис. 33
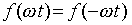, все B k=0; для нечетных функций, 
, все C k=0 и A 0=0.
Существует большое количество различных приближенных методов разложения на гармонические составляющие. Одним из простейших является метод прямоугольников, названный так потому, что в нем использован метод прямоугольников для вычисления интегралов в формулах (28). Этот метод предполагает замену с некоторым приближением интеграла суммой:
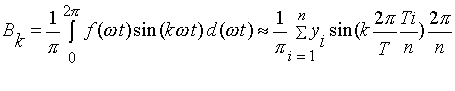
или
.
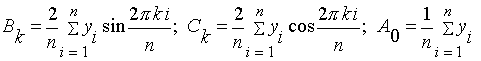В представленных формулах n - число разбиений периода исходной функции на равные части, y i - значение функции в конце интервала разбиения. Поскольку замена синусоидальной подынтегральной функции прямоугольником требует, чтобы на ширине прямоугольника синус слишком серьезно не изменялся, в методе прямоугольников число разбиений периода функции n должно не менее чем в два раза превышать максимальный номер вычисляемой гармоники. При этом вопрос о точности определения параметров гармоник не ставится; теорема Котельникова утверждает только, что при числе разбиений периода напряжения или тока, равном удвоенному номеру высшей гармоники, можно найти такие значения модулей и фаз гармоник, что в точках разбиения сумма членов конечного ряда Фурье будет точно равна значениям исходной функции.
Для кривой, симметричной относительно оси абсцисс, можно ограничиться суммированием только за полупериод, а полученный результат удвоить.
12.3. Расчет магнитного мешающего влияния
Поскольку влияющая цепь составлена несколькими межподстанционными зонами, то можно говорить о расчетной схеме по рис. 34, где показан усилительный участок линии связи между двумя усилительными пунктами. Этот участок соответствует n влияющим участкам тяговой сети с подключенными по их краям m генераторами гармонических составляющих тока и напряжения. Количество участков и генераторов в общем случае разное за счет возможного консольного питания некоторых участков, за счет того, что на переменном токе каждый электровоз является генератором гармоник, и за счет других причин. Расчет выполняют применительно к ближнему (дальнему) концу усилительного участка, например, УП1, полагая, что тяговая сеть состоит из плеч одностороннего питания, на конце каждого из которых находится один или несколько электровозов (при кратной тяге).
Рис. 34
Расчеты наведенного псофометрического напряжения шума производят путем расчета напряжения, наводимого от каждого участка на отдельной гармонике, с последующим квадратичным суммированием по всем гармоникам и квадратичным суммированием наводимых напряжений от всех участков.
Мешающее напряжение для k -ой гармоники от влияющего участка i вычисляют по формуле (30), учитывающей коэффициент акустического воздействия, коэффициент чувствительности, различие экранирующего действия параллельных проводников на разных частотах и большую электрическую длину провода связи:
(30)
В формуле (30) ωk=314 k рад/с - угловая частота k -ой гармоники тягового тока;
Mk - модуль взаимной индуктивности между контактной сетью и проводом связи для гармоники k, Гн/км;
Ik - эквивалентный ток k -ой гармоники тягового тока, А;
pk - коэффициент акустического воздействия для k -ой гармоники;
ηk - коэффициент чувствительности двухпроводной телефонной цепи к помехам для k -ой гармоники тягового тока;
s k - результирующий коэффициент экранирующего действия для k -ой гармоники тягового тока;
- коэффициент распространения канала провод линии связи - земля для k -ой гармоники, 
- комплексное число, составленное коэффициентом затухания и коэффициентом фазы;
103 - коэффициент перевода вольт в милливольты.
Формула (30) получается из уравнений, аналогичных уравнениям (3) и (4) раздела 2.1. Нетрудно заметить, что для электрически коротких линий, когда 
, формула (30) становится аналогичной формуле (19) для частоты 50 Гц с добавкой коэффициента акустического воздействия и коэффициента чувствительности.
Для коротких межподстанционных зон тяговой сети постоянного тока 3.3 кВ формулу (30) можно несколько упростить, полагая 
тогда
.
Для двухпроводных телефонных цепей определяют псофометрическое напряжение в диапазоне тональных частот (300 - 3400 Гц), суммируя гармоники от 7-й до 69-й при электрификации на переменном токе и от 2-й до 24-й при электрификации на постоянном токе:
.
Напряжения шума от нескольких влияющих плеч складывают по квадратичному закону
,
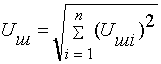где Uшi - напряжение шума, наводимое в линии связи от участка i.
РЕЗЮМЕ
При расчете напряжения мешающего влияния приходится учитывать большую длину линии связи и несинусоидальность влияющего тока, что приводит к необходимости суммирования напряжений влияния на разных участках и к расчету на гармониках. Учитывается обычно только магнитное влияние, а суммирование производится в квадратурах.
Возможность расчета на гармониках определяется теоремой Фурье и линейностью цепи, подверженной влиянию.
