4.1. Магнитное влияние при разных режимах работы смежной линии
Для анализа влияния режима смежного провода по отношению к земле рассмотрим те же три случая, что и для электрического влияния (рис. 7а, 7б, 7в). Чтобы оставить только магнитное влияние, предположим, что напряжение в контактной сети отсутствует, U к=0 (короткое замыкание). Емкости связи можно при этом не учитывать, поскольку они обычно существенно меньше емкостей провода на землю. На рис. 10 изображена двухячейковая схема для этого варианта, в которой нужно последовательно предполагать изолированный смежный провод, заземленный в начале смежный провод и заземленный с двух концов смежный провод.
Рис. 10
При изолированном от земли проводе схема замещения рис. 10 составлена двумя одинаковыми ячейками с половинными источниками ЭДС величиной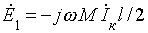 
. Эти два источника создают два контурных тока, изображенные на рисунке. Как нетрудно видеть, на среднем емкостном элементе суммарный ток равен нулю, следовательно, напряжение на изолированном проводе относительно земли посередине него равно нулю! Этот несколько неожиданный вывод следует из распределенности создаваемой магнитным полем продольной ЭДС вдоль всего провода и может быть проиллюстрирован на примере витка провода на стержне трансформатора (рис. 11).
Контактная сеть и смежный провод связаны друг с другом через магнитное поле и вполне могут рассматриваться как обмотки трансформатора без сердечника, с количеством витков обмоток по одному. При заземлении одного из зажимов катушки напряжение на втором зажиме по отношению к земле равно ЭДС в катушке. При заземлении средней точки катушки на зажимах будут два половинных противофазных напряжения, и такая же картина будет в случае подключения двух конденсаторов на выводы катушки без заземления средней точки. В последнем случае все равно, будет ли что-либо присоединено между средним выводом катушки и землей. Смежный провод отличается от витка трансформатора только более слабой магнитной связью с первичным витком - контактной сетью.
Рис. 11
Рис. 12
Собственно, картина распределения напряжения вдоль провода уже ясна; если дополнить ее соображением о линейной связи наводимой ЭДС с длиной смежного провода (поскольку площадь этого витка и магнитный поток внутри него растет прямо пропорционально длине провода), то распределение напряжения провод-земля вдоль смежного провода по рис. 12г понятно. Последний случай 3 (рис. 17в) соответствует нулевому напряжению относительно земли вдоль всего провода, если не учитывать сопротивление заземлений и активное сопротивление провода. Можно сослаться здесь на правило Ленца, согласно которому наведенные токи препятствуют изменению магнитного поля; можно снова взглянуть на рис. 11, представив ситуацию короткого замыкания витка. При коротком замыкании возникающий в витке ток пытается полностью скомпенсировать магнитное поле в стержне магнитопровода, и только жесткая связь через магнитное поле с первичной катушкой не позволяет этому свершиться, приводя к резкому росту тока вплоть до ограничений его индуктивностью рассеяния и активным сопротивлением витка. Для провода в зоне влияния контактной сети ток растет только до компенсации вызывающего ЭДС магнитного поля, а ток контактной сети вовсе не станет компенсировать этот рост из-за слабой обратной связи по магнитному полю.
Хотя на рис. 12г изображен график действующего значения напряжения, которое должно быть всегда положительным, для обозначения переворота фазы напряжения на нем изображена часть линии в отрицательной полуплоскости. То же самое сделано и на рис. 12д для величины тока в смежном проводе, графики которого располагаются ниже оси абсцисс в связи с положительным направлением тока слева направо на рис. 12а, 12б, 12в и знаком минус в формуле для ЭДС по закону электромагнитной индукции. При заземлении провода с двух сторон ток одинаков по всей длине провода (линия 3), а в остальных случаях, как это следует из более корректного рассмотрения, ток зависит от координаты по квадратичному закону.
Расчетным вариантом для магнитного влияния является случай заземления провода на конце, при котором напряжение в начале равно полной ЭДС в проводе, взятой с противоположным знаком:
(9)
Формула (9) не учитывает экранирующего действия рельсов и других протяженных проводников.
При сложном сближении отдельные напряжения, наводимые на участках косого или параллельного сближения, суммируются для вычисления напряжения в начале линии, поскольку соответствующие источники ЭДС включаются последовательно друг с другом.
4.2. Взаимная индуктивность между контактной сетью и смежным проводом Понятие взаимной индуктивности вводится в электротехнике как следствие закона электромагнитной индукции и закона полного тока. Для двух замкнутых контуров из тонких проводов, один из которых (первый) создает магнитное поле, а второй находится в этом поле, так что его площадку пересекает магнитный поток Φ от первого контура, взаимной индуктивностью называют магнитный поток Φ внутри второго контура, создаваемый током 1 А первого контура. При синусоидальных токах во втором контуре при этом наводится ЭДС, равная - jω Ф, то есть равная - jωM I к по определению взаимной индуктивности. Возможностью простого вычисления ЭДС и определяется ценность величины взаимной индуктивности M.
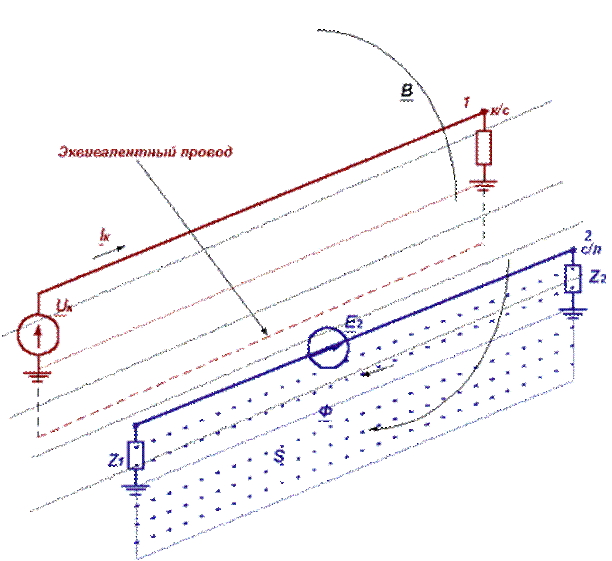<> Рис. 13
Использование этого понятия для смежного провода над землей допустимо с точки зрения упоминавшейся ранее возможности замены земли эквивалентным обратным проводом. Глубина его расположения по отношению к поверхности (бывшей) земли тем больше, чем больше глубина проникновения в землю электрического тока и соответственно магнитного поля, которая увеличивается при уменьшении удельной проводимости земли и уменьшении частоты тока. Поэтому величина M тем больше, чем меньше проводимость земли, и уменьшается для высших гармоник несинусоидального тока, будучи определяема величиной магнитного потока, пересекающего эквивалентную площадку S под смежным проводом (рис. 13). Поскольку удобнее относить величину взаимной индуктивности к 1 км смежного провода (и ко всей создающей магнитное поле контактной сети), то ее корректное определение будет звучать для контактной сети и смежного провода так.
Взаимной индуктивностью между контактной сетью и 1 км смежного провода называют величину магнитного потока, пронизывающего площадку под 1 км смежного провода в воздухе и в земле, при намагничивающем токе контактной сети 1 А.
Формулы для расчета взаимной индуктивности впервые были получены Карсоном и Поллачеком на основе решения задачи об электромагнитном поле провода над плоской поверхностью однородной земли. "Правила защиты..." [1,2] предлагают номограммы и графики для определения взаимной индуктивности, а также приближенную формулу (10):
, Гн/км,(10)
где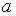 
- ширина сближения, м; 
- удельная проводимость земли, См/м;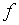 
- частота влияющего тока, Гц.
РЕЗЮМЕ
Протекание тока в контактной сети вызывает появление на смежном проводе напряжения магнитного влияния, которое максимально на одном из концов провода при заземлении на другом конце.
Расчетные формулы для вычисления напряжения магнитного влияния получаются из понятия взаимной индуктивности контуров контактная сеть - земля и смежный провод – земля
