1. Поезд массой 103 т, отходя от станции, развивает силу тяги 25×103 Н. Какой скорости достигает поезд на расстоянии 1 км, если сила сопротивления движению поезда составляет 0,005 веса поезда? Через какое время будет достигнута эта скорость?
2. На каком минимальном расстоянии от перекрестка должен начать тормозить автомобиль, движущийся со скоростью 72 км/ч, если коэффициент трения между шинами и дорогой 0,5?
3. Вагон массой 104 кг отцепился от движущегося состава и, двигаясь равнозамедленно, за 20 с прошел 20 м, после чего остановился. Найти силу трения, коэффициент трения и начальную скорость вагона.
4. Тело массой 0,1 кг, брошенное вертикально вверх со скоростью 40 м/с, достигло высшей точки подъема через 2,5 с. Определить среднюю силу сопротивления воздуха.
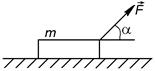Рис. 1.2.19
|
5. На тело массой m, лежащее на гладкой поверхности, в момент времени 
начала действовать сила, зависящая от времени по закону 
, где 
. Направление этой силы составляет угол 
с горизонтом (рис. 1.2.19). Найти скорость тела в момент отрыва от плоскости и путь, пройденный телом к этому моменту.
6. Тело массой 10 кг тянут по горизонтальной поверхности с силой 40 Н. Если эта сила приложена к телу под углом 60° к горизонту, оно двигается равномерно. С каким ускорением будет двигаться тело, если силу приложить под углом 30°? Трением пренебречь.
Рис. 1.2.20
|
7. По идеально гладкой поверхности ребенок тянет игрушку с силой 
Н под углом 
°. Игрушка состоит из двух тележек массами 
г и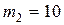 
г, соединенных невесомой нерастяжимой нитью (рис. 1.2.20). Найдите ускорение игрушки. Каково натяжение нити, соединяющей тележки? Трение не учитывать.
8. На тележке массой кг лежит груз массой 
кг. К грузу приложена сила F, сообщающая тележке с грузом ускорение a. Сила действует под углом 30° к горизонту. Каково максимальное значение этой силы, при котором груз не будет скользить по тележке? Коэффициент трения между грузом и тележкой m = 0,2. Трением между тележкой и дорогой пренебречь. С каким ускорением будет двигаться тележка под действием силы F?
9. Брусок массой 
кг может свободно скользить по горизонтальной поверхности без трения. На нем находится второй брусок массой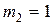 
кг. Коэффициент трения соприкасающихся поверхностей брусков m = 0,3. Определить максимальное значение силы 
, приложенной к нижнему бруску, при которой начинается соскальзывание верхнего бруска.
10. На горизонтальной поверхности находится брусок массой 
кг. Коэффициент трения бруска о поверхность m1 = 0,2. На бруске находится второй брусок массой 
кг. Коэффициент трения верхнего бруска о нижний m2 = 0,3. К верхнему бруску приложена сила F. Определить значение силы, при котором начнется совместное скольжение брусков по поверхности. При каком значении силы F 2 верхний брусок начнет проскальзывать относительно нижнего?
11. На наклонной плоскости с углом a при основании лежат один на другом два бруска с массами m 1 и m 2. Коэффициент трения между брусками m1, нижнего бруска m 1 о плоскость – m2. Оба бруска предоставлены себе. Найти соотношение между m1, m2 и a, при котором: а) оба бруска неподвижны; б) нижний брусок (m 1) скользит по верхнему; в) оба бруска скользят по поверхности с одинаковыми ускорениями; г) бруски движутся с разными ускорениями.
12. Предполагая массы грузов m 1 и m 2 известными, найти их ускорение в системе, состоящей из неподвижного блока А и подвижного блока В (рис. 1.2.21).
13. Через легкий вращающийся без трения блок перекинут шнур. На одном конце шнура висит груз массой m 1, а по другому с постоянным относительно шнура ускорением a 2 скользит кольцо массой m 2. Найти ускорение груза и силу трения кольца о шнур (рис.1.2.22).
14. В верхней части штанги установлен неподвижный блок, через который перекинута нить с грузами m 1 = 0,5 кг и m 2 = 0,1 кг (рис. 1.2.23). Во втором грузе есть отверстие, через которое проходит штанга. Сила трения этого груза о штангу равна 3 Н. Определить ускорение грузов и силу натяжения нити.
15. Система нитей и блоков представлена на рис.1.2.24. Считая нити и блоки лишенными массы и пренебрегая трением, выразите через 
и g ускорения грузов и силу натяжения нитей Т.
16. Через неподвижный блок А перекинута нить, на одном конце которой подвешен груз массой 
кг, а на другом конце – блок В (рис. 1.2.25). Через блок В перекинута нить, на которой подвешены грузы массами m 2 = 1 кг и m 3 = 2 кг. С каким ускорением будет двигаться блок В, если всю систему предоставить себе. Трение не учитывать.
17. Шайбу положили на наклонную плоскость и сообщили ей направленную вверх вдоль плоскости начальную скорость 
. Коэффициент трения между шайбой и
Рис. 1.2.21
Рис. 1.2.22
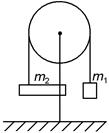Рис. 1.2.23
Рис. 1.2.24
Рис. 1.2.25
|
плоскостью равен m. При каком значении угла наклона a шайба пройдет вверх по плоскости наименьшее расстояние? Чему оно равно?
Рис. 1.2.26
Рис. 1.2.27
|
18. Небольшое тело m начинает скользить по наклонной плоскости из точки А, расположенной над вертикальным упором (рис. 1.2.26). Коэффициент трения между телом и наклонной плоскостью m = 0,14. При каком значении угла a время соскальзывания будет наименьшим?
19. В установке (рис. 1.2.27) известны угол a и коэффициент трения m между телом m 1 и наклонной плоскостью. Массы блока и нити пренебрежительно малы, трения в блоке нет. В начале оба тела неподвижны. Найти отношение масс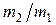 
, при котором тело m 2 начнет:а) опускаться; б) подниматься.
20. На горизонтальной поверхности тележки лежит груз массой m 1 = 2 кг, связанный с другим грузом массой m 2 = 1 кг с помощью тонкой нерастяжимой нити, перекинутой через блок, укрепленный на тележке (рис.1.2.28). С каким наибольшим ускорением нужно двигать тележку вправо, чтобы грузы находились в покое относительно нее? Коэффициент трения обоих грузов о поверхность тележки m = 0,1.
Рис. 1.2.28
Рис. 1.2.29
|
21. На наклонную плоскость, составляющую угол a с горизонтом, поместили два бруска массами m 1 и m 2. Коэффициенты трения между плоскостью и брусками соответственно m1 и m2, причем m1 > m2. Найти силу взаимодействия между брусками в процессе движения и значение угла a, при котором не будет скольжения (рис. 1.2.29).
22. Небольшое тело находится на наклонной плоскости с углом наклона a = 30°. Коэффициент трения между телом и плоскостью m = 0,1. С каким минимальным ускорением надо двигать наклонную плоскость в горизонтальном направлении, чтобы тело не скользило по ней? При каком значении ускорения тело начнет подниматься по наклонной плоскости?
23. Тело массой m лежит на наклонной плоскости с углом наклона 
°. Какой путь пройдет тело по наклонной плоскости за время t = 1 с, если наклонной плоскости сообщить ускорение a = 3,8 м/с2, направленное вертикально вниз? Коэффициент трения m = 0,2.
Рис. 1.2.30
|
24. Призме, на которой находится брусок массой m, сообщили направленное влево горизонтальное ускорение a (рис. 1.2.30). При каком максимальном значении этого ускорения брусок будет оставаться еще неподвижным относительно призмы, если коэффициент трения между ними 
?
25. На горизонтальной поверхности находится призма массой m 1 с углом a и на ней брусок массой m 2. Пренебрегая трением, найти ускорение призмы.
26. Катер массой 2 т трогается с места и в течение 10 с развивает при движении по спокойной воде скорость 
м/с. Определить силу тяги мотора,
считая ее постоянной. Сила сопротивления движению пропорциональна скорости 
, где k = 100 кг/с.
27. Начальная скорость пули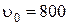 
м/с. При движении в воздухе за время 
= 0,8 с ее скорость уменьшилась до 
м/с. Масса пули m = 10 г. Считая силу сопротивления воздуха пропорциональной квадрату скорости, определить коэффициент сопротивления k. Действием силы тяжести пренебречь.
28. Парашютист, масса которого 80 кг, совершает затяжной прыжок. Считая, что сила сопротивления воздуха пропорциональна скорости, определить, через какое время D t скорость движения парашютиста будет равна 0,9 скорости установившегося движения. Коэффициент сопротивления 
=10 кг/с. Начальная скорость парашютиста равна нулю.
29. С вертолета, неподвижно висящего на некоторой высоте над поверхностью Земли, сброшен груз массой m = 100 кг. Считая, что сила сопротивления меняется пропорционально скорости, определить, через какое время D t ускорение a груза будет равно половине ускорения свободного падения. Коэффициент сопротивления =10 кг/с.
30. Катер массой m движется по озеру со скоростью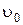 
. В момент 
выключили его двигатель. Считая силу сопротивления пропорциональной скорости, 
, найти: а) время движения катера с выключенным двигателем; б) скорость катера в зависимости от пути, пройденного с выключенным двигателем, а также полный путь до остановки.
31. Пуля, пробив доску толщиной h, изменила свою скорость от 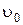до 
. Найти время движения пули в доске, считая силу сопротивления пропорциональной квадрату скорости.
32. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол a с горизонтом. Коэффициент трения зависит от пройденного пути x по закону 
, где g – постоянная. Найти путь, пройденный бруском до остановки, и максимальную скорость его на этом пути.
33. На горизонтальной плоскости с коэффициентом трения m лежит тело массой m. В момент к нему приложили горизонтальную силу, зависящую от времени как 
, где 
– постоянный вектор. Найти путь, пройденный телом за первые секунд действия этой силы.
34. Однородная тяжелая гибкая нить длиной 
лежит на наклонной плоскости призмы, расположенной под углом a к горизонту, так, что один конец нити свисает вдоль вертикальной грани призмы. При какой наименьшей длине свисающей части нить начнет скользить, сползая с призмы, если коэффициент трения m.
35. Велосипедист едет по круглой горизонтальной площадке радиусом R. Коэффициент трения зависит только от расстояния r от центра О площадки как 
, где m0 – постоянная. Найти радиус окружности с центром в точке О, по которой велосипедист может ехать с максимальной скоростью. Какова эта скорость?
36. Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорение в крайнем и нижнем положениях равны по модулю друг другу. Найти угол отклонения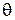 
нити в крайнем положении.
37. Подвешенный на нити длиной 
груз вращается в горизонтальной плоскости, причем нить отклоняется от вертикали на 20°. Каков период колебаний этого конического маятника, если = 1 м? Чему равно отношение периода колебаний конического маятника к периоду колебаний математического маятника той же длины?
Рис. 1.2.31
|
38. Тело массой m = 200 г, подвешенное на нити длиной = 80 см, отклонили от положения равновесия до высоты точки подвеса и отпустили, в результате чего нить оборвалась. На какой высоте находилось тело в момент разрыва нити, если нить разрывается под действием силы 
= 4 Н?
39. Тело массой движется по окружности в плоскости XZ (рис. 1.2.31). Тело массой 2 m находится на оси вращения (блок вращается с телом массой m). Пренебрегая массой нити и блока, а также трением в блоке, найдите период обращения тела массой m. Чему равен угол q?
