ЗАДАЧА 1. Найти модуль и направление силы, действующей на частицу массой m при ее движении в плоскости ХОY по закону x = A sinw t, y = B cosw t, где А, В, w – постоянные.
| ДАНО: m x = A sinw t y = B cosw t A = const B = const w= const |
F –?  –? –?
|
АНАЛИЗ. В задаче требуется определить силу, действующую на частицу, по известному закону движения. Движение частицы происходит в плоскости  , поэтому сила имеет две составляющие:
, поэтому сила имеет две составляющие:  и
и  , которые можно найти, вычислив проекции ускорения
, которые можно найти, вычислив проекции ускорения  и
и 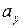 .
.
РЕШЕНИЕ. Дифференцируя дважды уравнения движения частицы по времени, находим составляющие ускорения по координатным осям:
 = – A w2sin
= – A w2sin  ,
, 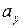 = – B w2cosw t.
= – B w2cosw t.
 Рис. 1.2.1
Рис. 1.2.1
|
По второму закону Ньютона сила равна  ,
,
тогда  и
и
 ,
,
где  – радиус-вектор частицы.
– радиус-вектор частицы.
Модуль силы равен 
где  – модуль радиус-вектора частицы.
– модуль радиус-вектора частицы.
Проверим размерность:  .
.
Вектор силы образует с отрицательным направлением оси ОХ угол a (рис. 1.2.1),  , и
, и 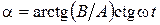 . Правильность формулы по размерности очевидна.
. Правильность формулы по размерности очевидна.
ОТВЕТ:  ;
; 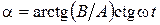 .
.
ЗАДАЧА 2. Аэростат массой  = 250 кг начал опускаться с ускорением
= 250 кг начал опускаться с ускорением  м/с2. Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением пренебречь.
м/с2. Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением пренебречь.
ДАНО:
 = 250 кг = 250 кг
 = 0,20 м/с2 = 0,20 м/с2
|
 –? –?
|
АНАЛИЗ. В задаче рассматривается движение аэростата, причем о его форме и размерах ничего не сказано. Это позволяет пренебречь формой и размерами аэростата и рассматривать его как материальную точку. В процессе движения на аэростат действуют две силы: сила тяжести  , направленная вертикально вниз, и сила Архимеда
, направленная вертикально вниз, и сила Архимеда  , направленная вертикально вверх. Начальная скорость аэростата равна нулю, поэтому он будет двигаться вертикально, и второй закон Ньютона удобно записать в проекциях на вертикальное направление.
, направленная вертикально вверх. Начальная скорость аэростата равна нулю, поэтому он будет двигаться вертикально, и второй закон Ньютона удобно записать в проекциях на вертикальное направление.
 Рис. 1.2.2
Рис. 1.2.2
|
При решении задачи уравнение динамики следует использовать дважды: для аэростата массой  , который опускается с ускорением
, который опускается с ускорением  , и для аэростата, сбросившего баласт и уменьшившего массу до значения
, и для аэростата, сбросившего баласт и уменьшившего массу до значения  , который поднимается с тем же по величине ускорением.
, который поднимается с тем же по величине ускорением.
РЕШЕНИЕ. Для опускающегося аэростата (рис. 1.2.2 а) по второму закону Ньютона имеем  проектируя на направление движения, получаем:
проектируя на направление движения, получаем:
 . (1.2.1)
. (1.2.1)
Если массу аэростата уменьшить на D m (рис. 1.2.2 б), то он будет двигаться вверх с ускорением  . Уравнение динамики в этом случае имеет вид:
. Уравнение динамики в этом случае имеет вид:
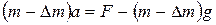 . (1.2.2)
. (1.2.2)
Решая совместно уравнения (1.2.1) и (1.2.2), получаем:  .
.
Проверка размерности  = (кг×(м/с2))/(с2×м) = кг. Подставив численные значения, получаем:
= (кг×(м/с2))/(с2×м) = кг. Подставив численные значения, получаем:  кг.
кг.
ОТВЕТ:  кг.
кг.
ЗАДАЧА 3. На тележке массой  = 20 кг, которая может свободно перемещаться вдоль горизонтальных рельсов, лежит брусок массой
= 20 кг, которая может свободно перемещаться вдоль горизонтальных рельсов, лежит брусок массой  = 5 кг (рис.1.2.3). Коэффициент трения между бруском и тележкой m = 0,2. Брусок тянут с силой
= 5 кг (рис.1.2.3). Коэффициент трения между бруском и тележкой m = 0,2. Брусок тянут с силой  , направленной параллельно рельсам. Найти ускорение бруска и тележки, если сила изменяется по закону
, направленной параллельно рельсам. Найти ускорение бруска и тележки, если сила изменяется по закону  , где
, где  Н/с. Построить графики зависимости найденных ускорений от времени.
Н/с. Построить графики зависимости найденных ускорений от времени.
ДАНО:
 = 20 кг = 20 кг
 = 5 кг
m = 0,2 = 5 кг
m = 0,2
 (Н)
с = 4,0 Н/с (Н)
с = 4,0 Н/с
|
 –? –?
|
 Рис. 1.2.3
Рис. 1.2.3
|
АНАЛИЗ. В задаче рассматривается поступательное движение двух соприкасающихся тел, между которыми действует сила трения. При некоторых значениях приложенной силы  брусок и тележка движутся вместе, с одинаковым ускорением, а при больших значениях силы
брусок и тележка движутся вместе, с одинаковым ускорением, а при больших значениях силы  брусок начинает обгонять тележку и будет скользить по ней. Если относительная скорость бруска (скорость бруска относительно тележки)
брусок начинает обгонять тележку и будет скользить по ней. Если относительная скорость бруска (скорость бруска относительно тележки)  равна нулю, то сила трения будет силой трения покоя и может принимать любое значение от 0 до
равна нулю, то сила трения будет силой трения покоя и может принимать любое значение от 0 до  = m N, т. е.
= m N, т. е.  тр.< m N, где
тр.< m N, где  – сила нормальной реакции при действии одного тела на другое. Если относительная скорость не равна нулю, то сила трения будет силой трения скольжения,
– сила нормальной реакции при действии одного тела на другое. Если относительная скорость не равна нулю, то сила трения будет силой трения скольжения,  тр = m N. Сила трения всегда направлена в сторону, противоположную относительной скорости. Поэтому силы трения, действующие на тележку
тр = m N. Сила трения всегда направлена в сторону, противоположную относительной скорости. Поэтому силы трения, действующие на тележку  и брусок
и брусок  , направлены так, как показано на рис. 1.2.3, причем
, направлены так, как показано на рис. 1.2.3, причем  =
=  . Помимо силы трения на тележку действуют сила тяжести
. Помимо силы трения на тележку действуют сила тяжести  , сила нормального давления бруска
, сила нормального давления бруска  и сила нормальной реакции рельсов
и сила нормальной реакции рельсов  . Эти силы вертикальны и взаимно компенсируют друг друга (рис.1.2.4):
. Эти силы вертикальны и взаимно компенсируют друг друга (рис.1.2.4):
 Рис. 1.2.4
Рис. 1.2.4
|
 .
.
Очевидно,  если
если 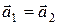 ;
;  и
и  , если
, если  ,
,  ,
,  где
где  и
и  – ускорения тележки и бруска относительно Земли. Оба этих вектора сонаправлены с силой
– ускорения тележки и бруска относительно Земли. Оба этих вектора сонаправлены с силой  : ускорение тележки возникает под действием одной силы трения
: ускорение тележки возникает под действием одной силы трения  , направленной так же, как и сила
, направленной так же, как и сила  , ускорение бруска не может быть направлено в противоположную сторону, т. к. сила трения не изменяет направления движения на обратное.
, ускорение бруска не может быть направлено в противоположную сторону, т. к. сила трения не изменяет направления движения на обратное.
 Рис. 1.2.5
Рис. 1.2.5
|
РЕШЕНИЕ. Уравнение динамики тел запишем в скалярной форме (для проекций на ось ОХ) (рис. 1.2.5):
 . (1.2.3)
. (1.2.3)
Если  , то из системы уравнений (1.2.3) получаем:
, то из системы уравнений (1.2.3) получаем:  .
.
В этом случае  и
и  , тогда
, тогда 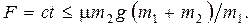 Правильность формулы по размерности очевидна.
Правильность формулы по размерности очевидна.
Таким образом, при  , ускорения обоих тел одинаковы, а сила трения покоя зависит от F. Решив систему (1.2.3) относительно a, получаем:
, ускорения обоих тел одинаковы, а сила трения покоя зависит от F. Решив систему (1.2.3) относительно a, получаем:
 (1.2.4)
(1.2.4)
– ускорения обоих тел пропорциональны t и меняются от 0 до  .
.
Проверим размерность:
 , подставив значение, получим:
, подставив значение, получим:  с;
с;  м/с2.
м/с2.
При t > t * ускорения тел различны, но сила трения постоянна и равна  . Тогда систему (1.2.3) перепишем в виде:
. Тогда систему (1.2.3) перепишем в виде:
 .
.
 Рис. 1.2.6
Рис. 1.2.6
|
Решая ее, получаем
 м/с2 ;
м/с2 ;
 . (1.2.5)
. (1.2.5)
Правильность размерности этих выражений очевидна. Из (1.2.5) следует, что ускорение  бруска растет линейно со временем, начиная от значения
бруска растет линейно со временем, начиная от значения
 м/с2.
м/с2.
График зависимости ускорений от времени можно построить на основании выражений (1.2.4) и (1.2.5). Этот график представлен на рис. 1.2.6.
ОТВЕТ: при  с
с  ; при
; при  с
с  м/с2,
м/с2,  .
.
ЗАДАЧА 4. В системе, показанной на рис. 1.2.7, массы тел равны m 0, m 1, m 2. Трения нет, массы блоков пренебрежительно малы. Найти ускорение тела m 1. АНАЛИЗ. В задаче рассматривается поступательное движение трех тел.
 Рис. 1.2.7
Рис. 1.2.7
|
На каждое из тел массами m 1 и m 2 действует сила тяжести ( и
и  соответственно) и сила натяжения нити
соответственно) и сила натяжения нити  . На тело массой m 0 действует сила натяжения нити
. На тело массой m 0 действует сила натяжения нити  в горизонтальном направлении (под действием этой силы тело движется с ускорением
в горизонтальном направлении (под действием этой силы тело движется с ускорением  относительно Земли), а также вертикальные силы тяжести и нормальной реакции, уравновешивающие друг друга. Нить, соединяющая тело массой m 0 с блоком B
относительно Земли), а также вертикальные силы тяжести и нормальной реакции, уравновешивающие друг друга. Нить, соединяющая тело массой m 0 с блоком B
нерастяжима и все время натянута, поэтому сила ее натяжения  одинакова по всей длине этой нити и равна силе, действующей на блок со стороны тел массами m 1 и m 2, т. е.
одинакова по всей длине этой нити и равна силе, действующей на блок со стороны тел массами m 1 и m 2, т. е.  = 2
= 2  . Блок В движется относительно Земли с ускорением
. Блок В движется относительно Земли с ускорением  , направленным вниз и численно равен
, направленным вниз и численно равен  . Кроме того, тела массами m 1 и m 2 движутся относительно блока В с ускорениями
. Кроме того, тела массами m 1 и m 2 движутся относительно блока В с ускорениями  . Для случая
. Для случая  >
>  направление
направление  указано на рис.1.2.7.
указано на рис.1.2.7.
Ускорение тела  равно векторной сумме этих ускорений
равно векторной сумме этих ускорений  . Для определения
. Для определения  и
и  следует записать уравнения динамики для каждого из тел и решить полученную систему уравнений.
следует записать уравнения динамики для каждого из тел и решить полученную систему уравнений.
РЕШЕНИЕ. Составим уравнения динамики для рассматриваемой системы тел в проекциях на оси системы координат:

Складывая все уравнения этой системы, получаем:
 (1.2.6)
(1.2.6)
Вычтем из второго уравнения третье 
Отсюда а 2 =  . (1.2.7)
. (1.2.7)
Подставив (1.2.7) в выражение (1.2.6) и решая относительно  , имеем:
, имеем:
 .
.
Тогда из (1.2.7)
а 2 =  .
.
Как следует из рис. 1.2.7, искомое ускорение  тела
тела  равно
равно  .
.
Правильность формулы по размерности очевидна.
ОТВЕТ:  .
.
ЗАДАЧА 5. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол a= 15° с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в  = 2 раза меньше времени спуска.
= 2 раза меньше времени спуска.
ДАНО
a= 15°

|
 –? –?
|
АНАЛИЗ. На тело, движущееся по наклонной плоскости (рис.1.2.8) действуют сила тяжести  , направленная вертикально вниз, сила нормальной реакции
, направленная вертикально вниз, сила нормальной реакции  , направленная перпендикулярно плоскости вверх, и сила трения
, направленная перпендикулярно плоскости вверх, и сила трения  , направленная противоположно движению: вниз по плоскости при подъеме (рис. 1.2.8 а) и вверх – при спуске (рис. 1.2.8 б). Уравнения динамики при подъеме и спуске в векторной форме имеют вид:
, направленная противоположно движению: вниз по плоскости при подъеме (рис. 1.2.8 а) и вверх – при спуске (рис. 1.2.8 б). Уравнения динамики при подъеме и спуске в векторной форме имеют вид:  причем сила трения в данном случае – сила трения скольжения, она равна
причем сила трения в данном случае – сила трения скольжения, она равна  .
.
 Рис. 1.2.8
Рис. 1.2.8
|
РЕШЕНИЕ. Рассмотрим подъем тела. Спроектируем уравнение движения на координатные оси (рис. 1.2.8 а)

откуда  и уравнение движения принимает вид:
и уравнение движения принимает вид:  .
.
Время подъема найдем из условия  . Получаем
. Получаем
 (1.2.8)
(1.2.8)
За время  тело прошло по плоскости путь
тело прошло по плоскости путь  , подставив
, подставив  и
и 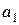 , получаем:
, получаем:
 . (1.2.9)
. (1.2.9)
При спуске тела (рис. 1.2.8 б) направление силы трения меняется на противоположное, поэтому уравнение движения принимает вид:  и ускорение равно
и ускорение равно
 . (1.2.10)
. (1.2.10)
Тело движется равноускоренно без начальной скорости и проходит путь  , определяемый согласно (1.2.9). Таким образом,
, определяемый согласно (1.2.9). Таким образом,  и время спуска равно
и время спуска равно  . Подставим в это выражение формулы (1.2.9) и (1.2.10):
. Подставим в это выражение формулы (1.2.9) и (1.2.10):
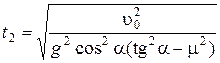 .
.
После преобразования получаем:
 . (1.2.11)
. (1.2.11)
По условию задачи  . Тогда, подставив
. Тогда, подставив 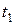 и
и  из (1.2.8) и (1.2.11),
из (1.2.8) и (1.2.11),
имеем: 
Решая уравнение относительно m, находим m = tga( – 1) / (h2 + 1).
– 1) / (h2 + 1).
Правильность формулы по размерности очевидна. Подставив значение, получим:  .
.
ОТВЕТ:  .
.
ЗАДАЧА 6. На вершине клина массой  3 = 10 кг расположен невесомый блок (рис. 1.2.9). Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы массами
3 = 10 кг расположен невесомый блок (рис. 1.2.9). Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы массами  1 = 1 кг и
1 = 1 кг и  2 = 10 кг. Коэффициенты трения грузов m 1 и m 2 о плоскости клина соответственно равны m1 = 0,2 и
2 = 10 кг. Коэффициенты трения грузов m 1 и m 2 о плоскости клина соответственно равны m1 = 0,2 и  , а коэффициент трения клина о горизонтальную поверхность
, а коэффициент трения клина о горизонтальную поверхность  . Углы плоскостей клина с горизонтальной плоскостью соответственно равны
. Углы плоскостей клина с горизонтальной плоскостью соответственно равны  ° и
° и  °. Определите силу натяжения нити.
°. Определите силу натяжения нити.
ДАНО:
 1 = 1 кг; m1 = 0,2 1 = 1 кг; m1 = 0,2
 2 = 10 кг 2 = 10 кг
 = 0,1 = 0,1
 3 = 10 кг 3 = 10 кг
 = 0,3
a1 = 30°; a2 = 60° = 0,3
a1 = 30°; a2 = 60°
|
| Т –? |
АНАЛИЗ. В задаче рассматривается поступательное движение трех тел. Тела m 1 и m 2 связаны нитью, и, если нить считать невесомой и нерастяжимой и пренебречь трением в блоке, то ускорения тел будут равны между собой. Действующие на тела силы трения со стороны клина не меняют направления движения тел, а лишь уменьшают ускорение и увеличивают силу натяжения нити. Поэтому для определения направления движения целесообразно рассмотреть вариант движения грузов без трения о грани клина, считая клин неподвижным. Далее следует рассмотреть движение грузов m 1 и m 2 с учетом сил трения между клином и грузами.
 Рис. 1.2.9
Рис. 1.2.9
|
На следующем этапе решения задачи имеющуюся систему уравнений динамики следует дополнить уравнением движения клина. Ускорение клина вызвано действием на него сил нормального давления грузов. Без выяснения направления движения клина нельзя правильно учесть действие силы трения между клином и плоскостью. Поэтому целесообразно сначала решить систему уравнений движения без учета этой силы, определить направление движения клина, а затем ввести в рассмотрение силу трения.
 Рис. 1.2.10
Рис. 1.2.10
|
РЕШЕНИЕ. Упростим задачу, а затем последовательно учтем сделанные упрощения. Будем считать, что клин неподвижен,  . Трение грузов о грани клина отсутствует: m1 = 0; m2 = 0. Определим направление движения грузов. На первое тело действуют (рис. 1.2.10) сила тяжести
. Трение грузов о грани клина отсутствует: m1 = 0; m2 = 0. Определим направление движения грузов. На первое тело действуют (рис. 1.2.10) сила тяжести  , сила нормальной реакции
, сила нормальной реакции  и сила натяжения нити
и сила натяжения нити  . На второе тело действуют силы тяжести
. На второе тело действуют силы тяжести  , нормальной реакции
, нормальной реакции  и натяжения нити
и натяжения нити  . Так как нить невесомая и нерастяжимая, и трение в блоке отсутствует, сила натяжения одинакова по всей длине нити, поэтому
. Так как нить невесомая и нерастяжимая, и трение в блоке отсутствует, сила натяжения одинакова по всей длине нити, поэтому  . Выберем направление движения. Пусть первое тело движется вверх, а второе вниз по грани клина. Спроектировав силы на направления движения, запишем уравнения динамики тел:
. Выберем направление движения. Пусть первое тело движется вверх, а второе вниз по грани клина. Спроектировав силы на направления движения, запишем уравнения динамики тел:

Учитывая, что модули ускорений тел относительно клина одинаковы, т. е.  , решив эту систему уравнений относительно
, решив эту систему уравнений относительно  , получаем:
, получаем:
 Рис. 1.2.11
Рис. 1.2.11
|


Размерность выражений очевидна. Подставив значения  ,
,  и a1, a2, получаем
и a1, a2, получаем  м/с2;
м/с2;
 » 12,4 Н. Т. к.
» 12,4 Н. Т. к.  1 > 0, то направление движения выбрано правильно.
1 > 0, то направление движения выбрано правильно.
На следующем этапе решения задачи будем учитывать трение тел  и m 2 о клин. Сила трения не меняет направления движения, а только замедляет его, и направлена противоположно движению (рис. 1.2.11). С учетом сил трения уравнения динамики тел принимают вид в выражениях:
и m 2 о клин. Сила трения не меняет направления движения, а только замедляет его, и направлена противоположно движению (рис. 1.2.11). С учетом сил трения уравнения динамики тел принимают вид в выражениях:
 (1.2.12)
(1.2.12)
Здесь  (см. задачу 5). Решая эту систему относительно
(см. задачу 5). Решая эту систему относительно  и
и  , получаем:
, получаем:

Сила натяжения равна
 Рис. 1.2.12
Рис. 1.2.12
|

Размерность выражения очевидна. Подставив значения входящих в эти формулы величин, имеем
 2 » 6,62 м/с2,
2 » 6,62 м/с2,  » 13,2 Н, т. е. ускорение уменьшилось вследствие трения, а сила натяжения увеличилась.
» 13,2 Н, т. е. ускорение уменьшилось вследствие трения, а сила натяжения увеличилась.
Будем считать теперь, что клин может без трения перемещаться по поверхности,  . На клин действуют (рис.1.2.12) сила тяжести
. На клин действуют (рис.1.2.12) сила тяжести  , сила нормальной реакции
, сила нормальной реакции  , а также силы давления
, а также силы давления  и
и  тел m 1 и m 2. Эти силы направлены противоположно реакциям
тел m 1 и m 2. Эти силы направлены противоположно реакциям  и
и  и равны им
и равны им  ,
,  . Запишем уравнения динамики для клина в координатах ХОY (рис.1.2.12), учитывая, что перемещение клина возможно только в направлении оси Х:
. Запишем уравнения динамики для клина в координатах ХОY (рис.1.2.12), учитывая, что перемещение клина возможно только в направлении оси Х:
 (1.2.13)
(1.2.13)
 Рис. 1.2.13
Рис. 1.2.13
|
Мы получили систему из двух уравнений с четырьмя неизвестными  , N 3, P 1 и P 2, где а 3 ускорение клина относительно Земли.
, N 3, P 1 и P 2, где а 3 ускорение клина относительно Земли.
Для нахождения замкнутой системы уравнений исследуем движение грузов  и
и  относительно клина. Так как клин движется ускоренно, то связанная с ним система отсчета неинерциальна. Чтобы записать второй закон Ньютона для каждого из тел, необходимо к действующим на эти тела силам добавить еще силу инерции (рис.1.2.13):
относительно клина. Так как клин движется ускоренно, то связанная с ним система отсчета неинерциальна. Чтобы записать второй закон Ньютона для каждого из тел, необходимо к действующим на эти тела силам добавить еще силу инерции (рис.1.2.13):
 ;
;  .
.
Проектируя силы инерции на направления движения  , с учетом уравнений (1.2.12), получаем:
, с учетом уравнений (1.2.12), получаем:
 (1.2.14)
(1.2.14)
Спроектируем силы на направления, перпендикулярные  . Учитывая, что P 1 = N 1; P 2 = N 2, имеем:
. Учитывая, что P 1 = N 1; P 2 = N 2, имеем:
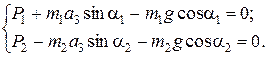 (1.2.15)
(1.2.15)
Уравнения (1.2.13), (1.2.14) и (1.2.15) представляют собой искомую замкнутую систему из шести уравнений с шестью неизвестными:  ,
,  , T, P 1, P 2, N 3. Выразим из (1.2.15) P 1 и P 2 и подставим в первое уравнение системы (1.2.13), получаем:
, T, P 1, P 2, N 3. Выразим из (1.2.15) P 1 и P 2 и подставим в первое уравнение системы (1.2.13), получаем:
 ;
;
 ;
;
 .
.
Складывая уравнения (1.2. 14), находим  :
:
 .
.
Тогда  , размерность очевидна, подставив значение, получим:
, размерность очевидна, подставив значение, получим:  Н.
Н.
ОТВЕТ:  Н.
Н.
ЗАДАЧА 7. Замкнутая однородная цепочка массой m = 0,4 кг, надетая вплотную на гладкий круговой конус с углом полураствора  °, вращается вокруг оси конуса с угловой скоростью w= 10 с–1 (рис. 1.2.14 а). При этом цепочка образует окружность, радиус которой r = 10 см. Найти силу натяжения цепочки.
°, вращается вокруг оси конуса с угловой скоростью w= 10 с–1 (рис. 1.2.14 а). При этом цепочка образует окружность, радиус которой r = 10 см. Найти силу натяжения цепочки.
 Рис. 1.2.14 а
Рис. 1.2.14 а
|
ДАНО:
m = 0,4 кг
 °
w= 10 с–1
r = 10 см °
w= 10 с–1
r = 10 см
|
| T –? |
АНАЛИЗ. Для нахождения силы натяжения цепочки, т. е. силы, с которой один ее элемент действует на другой, рассмотрим движение произвольного элемента D  с массой D m. Этот элемент движется в горизонтальной плоскости по окружности радиуса r с постоянной по модулю скоростью
с массой D m. Этот элемент движется в горизонтальной плоскости по окружности радиуса r с постоянной по модулю скоростью  . На элемент D
. На элемент D  действует сила тяжести
действует сила тяжести  , сила нормальной реакции конуса
, сила нормальной реакции конуса  (рис. 1.2.14 а), а также силы натяжения
(рис. 1.2.14 а), а также силы натяжения  и
и  со стороны элементов, соседних с выбранным. Эти силы направлены по касательной к окружности, образуемой цепочкой, в точках, где расположены концы элемента D
со стороны элементов, соседних с выбранным. Эти силы направлены по касательной к окружности, образуемой цепочкой, в точках, где расположены концы элемента D  . Второй закон Ньютона для элемента D
. Второй закон Ньютона для элемента D  имеет вид:
имеет вид:

Вследствие полной симметрии все элементы, составляющие цепочку, находятся в совершенно одинаковых условиях, поэтому  .
.
РЕШЕНИЕ. Координатные оси выберем как показано на рис. 1.2.14 а. Ясно, что  ;
;  ;
;  .
.
Спроектируем уравнение динамики на координатные оси
 (1.2.16)
(1.2.16)
 Рис. 1.2.14 б
Рис. 1.2.14 б
|
Здесь Da – центральный угол, соответствующий элементу дуги  . Тогда
. Тогда  .
.
Решая совместно первые два уравнения системы (1.2.16) и учитывая, что,  , получим:
, получим:

откуда
 . (1.2.17)
. (1.2.17)
Цепочка однородная, масса m равномерно распределена по ее длине, поэтому  .
.
Элемент  мал, следовательно, угол Da также мал и sin(Da/2)» Da/2.
мал, следовательно, угол Da также мал и sin(Da/2)» Da/2.
Подставив полученные выражения для D m и sin(Da/2) в уравнение (1.2.17), получим
 .
.
Проверим размерность: [ Т ] = кг×м/с2 = Н. Подставив значение, получим:  Н.
Н.
ОТВЕТ:  Н.
Н.
ЗАДАЧА 8. Над горизонтальным столом, касаясь его нижним концом, вертикально висит тонкий однородный шнур массой  и длины
и длины 
(рис. 1.2.15). Верхний конец шнура освобождают. Найти силу давления шнура на стол в процессе падения как функцию длины уже лежащей на столе части шнура и как функцию времени.
ДАНО:
 (кг) (кг)
 (м) (м)
|
| h –? |
АНАЛИЗ. Если бы не было стола, шнур после освобождения его верхнего конца двигался бы в состоянии невесомости (при отсутствии сил сопротивления воздуха). Это значит, что в любой момент времени все элементы шнура обладали бы одинаковыми скоростями и ускорениями, равными  . Никаких деформаций и сил натяжения не возникало бы. Если предположить, что шнур мягкий, то при падении его нижней части на стол обусловленная этим падением деформация не вызовет появления сил натяжения в шнуре, и свободная часть шнура будет двигаться так же, как если бы не было стола. В процессе падения шнура длина
. Никаких деформаций и сил натяжения не возникало бы. Если предположить, что шнур мягкий, то при падении его нижней части на стол обусловленная этим падением деформация не вызовет появления сил натяжения в шнуре, и свободная часть шнура будет двигаться так же, как если бы не было стола. В процессе падения шнура длина  лежащей на столе части непрерывно возрастает, при этом каждый элемент
лежащей на столе части непрерывно возрастает, при этом каждый элемент  , приходящий в соприкосновение со столом, полностью теряет скорость, которую он приобрел во время свободного падения (удар такого элемента о стол надо считать абсолютно неупругим). По изменению импульса этого элемента можно определить силу действия стола на него и, следовательно, силу
, приходящий в соприкосновение со столом, полностью теряет скорость, которую он приобрел во время свободного падения (удар такого элемента о стол надо считать абсолютно неупругим). По изменению импульса этого элемента можно определить силу действия стола на него и, следовательно, силу  , с которой данный элемент давит на стол. Полная сила давления шнура
, с которой данный элемент давит на стол. Полная сила давления шнура  на стол в процессе падения складывается из силы
на стол в процессе падения складывается из силы  и силы тяжести
и силы тяжести  лежащей на столе части шнура:
лежащей на столе части шнура:
 , (1.2.18)
, (1.2.18)
Для определения силы  необходимо определить импульс, приобретаемый элементом
необходимо определить импульс, приобретаемый элементом  к моменту его соприкосновения со столом.
к моменту его соприкосновения со столом.
 Рис. 1.2.15
Рис. 1.2.15
|
РЕШЕНИЕ. Ось ОY направим вертикально вниз (по движению шнура), за начало отсчета примем точку подвеса шнура (рис.1.2.15).
Рассмотрим, что происходит за некоторый произвольный промежуток времени  . На рис. 1.2.15 показаны положения шнура в моменты времени
. На рис. 1.2.15 показаны положения шнура в моменты времени 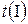 и
и  . За время
. За время  верхний конец шнура сместится вниз на расстояние
верхний конец шнура сместится вниз на расстояние  . К моменту времени
. К моменту времени  скорость любой точки шнура
скорость любой точки шнура
 , (1.2.19)
, (1.2.19)
где  – расстояние, пройденное за время
– расстояние, пройденное за время  как верхним концом шнура, так и любым другим элементом, в том числе и элементом
как верхним концом шнура, так и любым другим элементом, в том числе и элементом  , который за время
, который за время  ударился о стол. Ясно, что
ударился о стол. Ясно, что  , где
, где  – длина той части шнура, которая лежит на столе. Очевидно, что сила, действующая на элемент
– длина той части шнура, которая лежит на столе. Очевидно, что сила, действующая на элемент  со стороны стола, равна:
со стороны стола, равна: 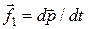 , где
, где  – изменение импульса элемента
– изменение импульса элемента  за время
за время  . Тогда сила, действующая на стол со стороны элемента
. Тогда сила, действующая на стол со стороны элемента  , равна
, равна
 (1.2.20)
(1.2.20)
Изменение импульса элемента  , где
, где 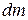 – масса элемента,
– масса элемента,  – скорость, которой он обладал перед ударом, т. е. в момент времени
– скорость, которой он обладал перед ударом, т. е. в момент времени  . Знак «минус» объясняется тем, что конечный импульс элемента равен нулю. Перепишем уравнение (1.2.20) в скалярной форме, получаем:
. Знак «минус» объясняется тем, что конечный импульс элемента равен нулю. Перепишем уравнение (1.2.20) в скалярной форме, получаем:
 . (1.2.21)
. (1.2.21)
Масса элемента  равна
равна  . С учетом (1.2.19) изменение проекции импульса за время
. С учетом (1.2.19) изменение проекции импульса за время  определяется выражением:
определяется выражением:
 . (1.2.22)
. (1.2.22)
Подставив (1.2.22) в (1.2.21), получаем:  Однако
Однако  – скорость любой точки шнура, тогда
– скорость любой точки шнура, тогда

В начальный момент шнур касался поверхности стола:  ; в момент времени
; в момент времени  :
:  . Тогда масса этой части шнура
. Тогда масса этой части шнура  =
=  0
0  /
/  0. Спроектировав векторное уравнение (1.2.18) на ось ОY и подставив значения
0. Спроектировав векторное уравнение (1.2.18) на ось ОY и подставив значения  и
и  , получаем:
, получаем:

– в любой момент времени при 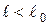 сила давления шнура на стол втрое больше силы тяжести той части шнура, которая к этому моменту уже лежит на столе.
сила давления шнура на стол втрое больше силы тяжести той части шнура, которая к этому моменту уже лежит на столе.
Представим теперь  как функцию времени. Ясно, что
как функцию времени. Ясно, что 
тогда  .
.
Проверим размерность:  .
.
Следовательно, при падении шнура на стол сила давления растет пропорционально квадрату времени.
ОТВЕТ:  .
.
ЗАДАЧА 9. Парашютист массой  = 100 кг делает затяжной прыжок с начальной скоростью
= 100 кг делает затяжной прыжок с начальной скоростью  . Найти закон изменения его скорости до раскрытия парашюта, если сила сопротивления воздуха пропорциональна скорости движения парашютиста:
. Найти закон изменения его скорости до раскрытия парашюта, если сила сопротивления воздуха пропорциональна скорости движения парашютиста:  , где
, где  = 20 кг/с.
= 20 кг/с.
ДАНО:
 = 100 кг = 100 кг
 м/с м/с
 (Н) (Н)
 = 20 кг/с = 20 кг/с
|
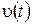 –? –?
|
АНАЛИЗ. Эта задача на динамику тела под действием переменной силы. Сила сопротивления воздуха является функцией скорости, поэтому, представив ускорение тела как производную от скорости по времени, на основании второго закона Ньютона получим дифференциальное уравнение первого порядка, решение которого даст закон изменения скорости со временем.

| 
|
Рис. 1.2.16 Рис. 1.2.17
РЕШЕНИЕ. На парашютиста действуют сила тяжести  , направленная вниз, и сила сопротивления
, направленная вниз, и сила сопротивления  , направленная вверх (рис. 1.2.16). По второму закону Ньютона имеем:
, направленная вверх (рис. 1.2.16). По второму закону Ньютона имеем:  .
.
Разделяя переменные, получаем дифференциальное уравнение первого порядка относительно  :
:  ,которое можно представить в виде:
,которое можно представить в виде:  .
.
После интегрирования получаем: 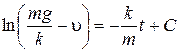 . (1.2.23)
. (1.2.23)
Постоянную С определяем из начальных условий: в момент времени  скорость парашютиста
скорость парашютиста  , отсюда
, отсюда  . Подставляя значение С в выражение (1.2.23) и потенцируя, получаем:
. Подставляя значение С в выражение (1.2.23) и потенцируя, получаем:
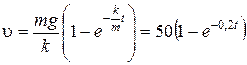 .
.
Проверим размерность:  . Это искомый закон изменения скорости. Из него следует, что при
. Это искомый закон изменения скорости. Из него следует, что при  скорость стремится к максимальному значению
скорость стремится к максимальному значению  м/с.
м/с.
Усложним задачу. Пусть начальная скорость парашютиста направлена горизонтально:  , где
, где  – орт оси ОX (рис. 1.2.17). Тело движется по кривой, скорость в любой момент времени направлена по касательной к траектории вниз, а сила – противоположно скорости.
– орт оси ОX (рис. 1.2.17). Тело движется по кривой, скорость в любой момент времени направлена по касательной к траектории вниз, а сила – противоположно скорости.
По второму закону Ньютона имеем:  ;
;  .
.
Разделяя переменные, получаем:  ;
;  .
.
Интегрируя, учитывая начальные условия (при  ;
;  ;
;  ) и затем потенцируя, получаем закон изменения скорости:
) и затем потенцируя, получаем закон изменения скорости:  ;
;  .
.
Проверка размерности аналогична предыдущей.
ОТВЕТ:  .
.
ДАНО:
 (Н); (Н);  (Н/с) (Н/с)
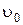 (м/с); (м/с);  (кг) (кг)
|
 –? –?
|
ЗАДАЧА 10. Двигатель тормозной системы развивает силу тяги, пропорциональную времени:  , где
, где  . Пренебрегая трением, определить, через сколько времени от момента включения тормозного двигателя тело массой m, на котором установлен такой двигатель, остановится. В момент включения двигателя скорость тела составляла
. Пренебрегая трением, определить, через сколько времени от момента включения тормозного двигателя тело массой m, на котором установлен такой двигатель, остановится. В момент включения двигателя скорость тела составляла 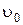 . Считать, что масса двигателя много меньше массы тела.
. Считать, что масса двигателя много меньше массы тела.
 АНАЛИЗ. Задача на динамику тела под действием переменной силы – силы тяги тормозного механизма, которая является функцией времени. Для определения времени торможения необходимо записать второй закон Ньютона, представив ускорение как производную скорости по времени, найти закон изменения скорости (движение одномерное, скорость меняется от значения
АНАЛИЗ. Задача на динамику тела под действием переменной силы – силы тяги тормозного механизма, которая является функцией времени. Для определения времени торможения необходимо записать второй закон Ньютона, представив ускорение как производную скорости по времени, найти закон изменения скорости (движение одномерное, скорость меняется от значения 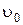 до нуля, т.е не меняет своего направления, поэтому проекция скорости на направление движения равна модулю скорости в любой момент времени) и, приравняв скорость нулю, найти время.
до нуля, т.е не меняет своего направления, поэтому проекция скорости на направление движения равна модулю скорости в любой момент времени) и, приравняв скорость нулю, найти время.
РЕШЕНИЕ. Движение тела прямолинейное замедленное, уравнение движения по второму закону Ньютона имеет вид:  .
.
Разделяя переменные, получаем дифференциальное уравнение:  .
.
Проинтегрировав, имеем:  .
.
Подставив начальные условия ( при
при  ), найдем
), найдем  ,
,
тогда  (1.2.24)
(1.2.24)
– это закон изменения скорости во времени. В момент времени  тело остановится,
тело остановится,  , отсюда
, отсюда  .
.
Проверим размерность:  .
.
ОТВЕТ:  .
.






