РАСЧЁТ
ЗАКРЫТЫХ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ ПЕРЕДАЧ
Методические указания по курсу "Детали машин и основы конструирования"
Для студентов специальностей 150700 - Локомотивы
150800 - Вагоны
170900 - Подъёмно-транспортные,
строительные и
дорожные машины и
оборудование
181400 - Электрический транспорт
железных дорог.
Составители: Толстоногов А.А.,
Янковский В.В.,
Фёдоров В.В.,
Назарова Н.В.
Самара 2004 г.
УДК 621.81.
Методические указания к выполнению расчётно-графических работ и курсового проекта по дисциплине "Детали машин" для студентов специальностей 150700, 150800, 170900 / Составители Толстоногов А.А., Янковский В.В., Фёдоров В.В., Назарова Н.В. Самара, СамГАПС, 2004.- 18 с.
Утверждено на заседании кафедры, протокол №8 от 11 мая2004г.
Печатается по решению редакционно-издательского совета академии.
Составители: Толстоногов Андрей Арленович,
Янковский Виктор Владимирович,
Фёдоров Виктор Васильевич,
Назарова Надежда Владимировна.
Рецензенты: Доцент кафедры ОКМ СГАУ Васин В.Н.
Доцент кафедры механики СамИИТ Глобенко Е.В.
Редактор: Шимина И.А.
Подписано в печать 33.33.2002 Формат 60х84 1.16
Бумага писчая. Усл. п. л. 1,13
Тираж 400 экз. Заказ №
© Самарская Государственная Академия Путей Сообщения, 2004.
ОГЛАВЛЕНИЕ
Введение..................................... 3
1. МЕТОДИКА РАСЧЕТА ПЕРЕДАЧИ................... 4
2.ПРИМЕР РАСЧЕТА ПЕРЕДАЧИ..................... 9
ЛИТЕРАТУРА................................. 13
ПРИЛОЖЕНИЕ................................ 14
ВВЕДЕНИЕ
Цилиндрические зубчатые передачи являются наиболее распространенными механическими передачами и механизмами самых различных машин, приборов и приспособлений. Размеры, вес и материалы зубчатых колес зачастую определяют габариты и стоимость всего механизма.
Поэтому важнейшей задачей проектирования является выбор материала зубчатых колес и определение их минимальных размеров при условии обеспечения работоспособности передачи в течение требуемого срока службы.
В настоящее время при проектировании отдается предпочтение закрытым зубчатым передачам, выполняемым в герметичных корпусах, в которых обеспечивается постоянный подвод смазывающего материала и защита от попадания механических примесей на рабочие поверхности зубьев.
В таких условиях работы практически исключается абразивный износ и предупреждается заедание поверхностей зубьев, а основными видами разрушения зубчатых колес являются усталостное выкрашивание поверхностей зубьев от действия переменных контактных напряжений и поломка зубьев в результате образования усталостной трещины от действия переменных напряжений при изгибе.
Таким образом, критериями прочности закрытых передач являются обеспечение контактной прочности боковых поверхностей зубьев и прочность зубьев на изгиб при действии переменных напряжений.
В настоящих методических указаниях излагается методика расчета закрытых цилиндрических прямозубых и косозубых эвольвентных некоррегированных зубчатых передач. Методика включает в себя проектный расчет межосевого расстояния из условия усталостной контактной прочности поверхностей зубьев, расчет геометрических параметров колес по ГОСТ 16532-70, ГОСТ 16530-83 и ГОСТ 16531-83 и проверочные расчеты зубьев на выносливость по контактным напряжениям и напряжениям изгиба в соответствии с ГОСТ 21354-75
Приведен контрольный пример расчета.
Для успешного использования компьютерной программы расчёта закрытых цилиндрических передач студент предварительно должен усвоить теоретический материал и разобраться в порядке и принципах расчета.
1. МЕТОДИКА РАСЧЕТА ПЕРЕДАЧИ.
Исходными данными для расчета являются требуемое передаточное отношение, передаваемые моменты на валах шестерни и колеса, частоты ращения шестерни и колеса, ресурс передачи, т.е. время работы передачи за срок службы механизма.
Расчет закрытой цилиндрической зубчатой передачи производится в следующей последовательности.
1.1. Выбирается материал для изготовления зубчатых колес.
При выборе материалов шестерни и колеса следует руководствоваться данными, приведенными в Приложении. Рекомендуется выбирать материалы и упрочняющую технологию таким образом, чтобы твердость поверхности зубьев шестерни была больше твердости зубьев колеса не менее, чем на 20…30 НВ.
1.2. Определяются допускаемые напряжения с учетом фактических условий нагружения зубьев колеса и шестерни
[σ н ] i = (σ н lim bi / Sнi) · KнLi ·[σ k ] i = (σ0 F lim bi / SF i) · KFCi · KFLi,
где i = 1,2 – индекс; i = 1 –для шестерни, i = 2 –для колеса;
σн lim bi - предел контактной выносливости;
σ F lim bi - предел выносливости на изгиб при отнулевом цикле
изменения напряжений;
Sнi - коэффициент безопасности при расчете на контактную
прочность зубьев;
SFi - коэффициент безопасности при расчете зубьев на изгиб.
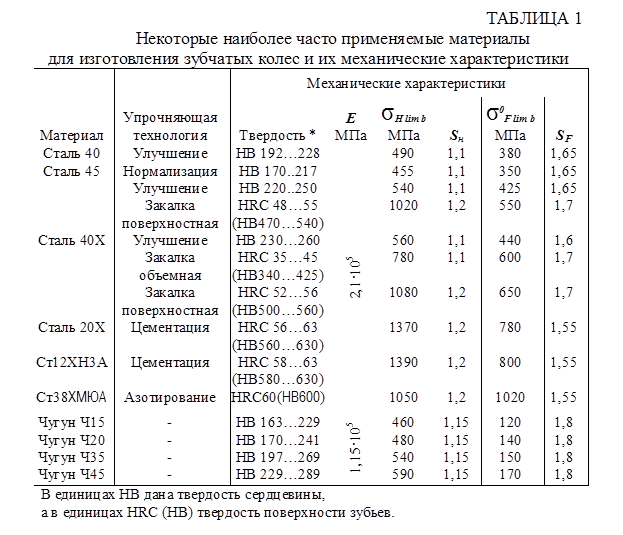
Величины σ н lim bi и σ F lim bi для различных материалов приведены в таблице 1.
Коэффициенты долговечности KHL и KFL учитывают влияние ресурса и режима нагрузки передачи.
KHLi = (NHOi / NHEi)1/6; KFLi = (NFOi / NFEi)1/ m;
где NHOi, NFOi - базовые числа циклов напряжений;
NHEi, NFEi - расчетное число циклов напряжений;
m = 6 - для зубчатых колес из незакаленных сталей и других
мягких материалов (НВ < 350);
m = 9 - для зубчатых колес из закаленных сталей (НВ > 350).
При расчете на контактную прочность зубьев принимается NHOi = 30 НВ.
При расчете на изгиб зубьев колес, выполненных из сталей, принимается NFOi = 4·106, для зубчатых колес из других материалов NFOi = 3·106.
При постоянном режиме нагрузки, который является наиболее тяжелым для механизма, расчетное число циклов напряжений равно фактическому числу циклов нагружений каждого зуба за срок службы механизма и с учетом того, что за каждый оборот колеса каждый зуб испытывает один цикл нагружений, определяется
NHEi = NFEi = 60· ni · tΣ,
где ni - частота вращения зубчатого колеса, об/мин;
tΣ, – время работы передачи за срок службы (ресурс передачи), часы;
tΣ = L · 365 · Кгод · 24 · Ксут,, L - срок службы, годы;
Кгод, Ксут – коэффициенты использования передачи в году и сутках.
Если NHEi > NHOi или NFEi > NFOi, то принимают соответственно KHLi =1 и KFLi =1.
Если KHLi = (NHOi / NHEi)1/6 ≥2,4, то для расчета принимается KHLi = 2,4.
Если KFLi =(NFOi / NFEi)1/6 ≥2, то для расчета принимается KFLi = 2.
Если KFLi =(NFOi / NFEi)1/9 ≥1,6, то для расчета принимается KFLi = 1,6.
При переменном режиме нагрузки, который характеризуется циклограммой изменения нагрузки (крутящего момента) во времени, за расчетную нагрузку принимается максимальная по циклограмме, а расчет коэффициентов KHL и KFL ведется по эквивалентным числам циклов напряжений. Методы определения NHE и NFE при переменных режимах нагрузки подробно изложены в работах [1,2, 3]. Коэффициент KFCi учитывает влияние двустороннего приложения нагрузки (например, реверсивные передачи):
KFCi = 1 – односторонняя нагрузка;
KFCi = 0,7…0,8 – реверсивная нагрузка.
1.3. Определяются числа зубьев шестерни, колеса и передаточное число.
Число зубьев шестерни по условию отсутствия подрезания для прямозубых колес должно быть Z1 > 17, а для косозубых и шевронных колес Z1 > 17· cos³ β.
Число зубьев колеса Z2 = Z1 · i12,
где i12 – требуемое передаточное отношение передачи (отношение
угловых скоростей шестерни и колеса);
β - угол наклона линии зуба принимается для косозубых колес в
интервале (8…15º), для шевронных – (25…45º)
Передаточное число u = Z2 / Z1 определяется по найденным значениям Z1 и Z2, округленных до целых чисел, и не должно отличаться от требуемого передаточного отношения не более, чем на 3%.
1.4. Определяется требуемое межосевое расстояние передачи из условия контактной прочности поверхностей зубьев
аw = (u +1){0,78 · М2 · Кн ·cos β. · Е1 · Е2 /([σ н ] · u)2 Ψbа · (Е 1+ Е2)}1/3,
где М2 – крутящий момент на колесе, Н·мм;
Ψbа – коэффициент ширины зубчатого колеса, выбирается по таблице 2;
Кн - коэффициент нагрузки, учитывающий дополнительные вредные
нагрузки, сопутствующие работе передачи; предварительно
принимается Кн = 1,2 для колес с твердостью поверхностей
зубьев < НВ 350 и Кн = 1,35 с твердостью НВ 350;
Е1, Е2 – модули упругости первого рода соответственно материала
шестерни и колеса;
[σ н ] - расчетное допускаемое контактное напряжение.
Расчетное допускаемое контактное напряжение определяется следующим образом:
при расчете прямозубых колес (β = 0) [σ н ] = [σ н ] min,
при расчете косозубых колес (β ≠ 0) и в случаях большой разности твердостей зубьев прямозубых шестерни и колеса (НВ1 – НВ2 ≥70)
[σ н ] = 0,45 ([σ н ] 1 + [σ н ] 2),
где [σ н ] 1, [σ н ] 2 – допускаемые контактные напряжения соответственно
для зубьев шестерни и колеса;
[σ н ] min - минимальное из двух значений [σ н ] 1 и [σ н ] 2
Следует иметь в виду, что в любом случае должно выполняться условие [σ н ] < 1,23 · [σ н ] min.
1.5. Определяется нормальный модуль передачи
mn =2 аw · cos β /(Z1 + Z2)
Полученное значение mn округляют до ближайшего стандартного по СТ СЭВ 310-76 (см. таблица 3).
1.6. Уточняется межосевое расстояние передач
аw = 0,5 (Z1 + Z2) m n /cos β.
За результат определения уточненного принимается целая часть полученного значения. При проектировании стандартных редукторов полученное значение округляют до ближайшего значения параметрического ряда по таблице 4.
1.7. Для косозубой передачи уточняется угол наклона линии зуба
β = arcos [0,5 (Z1 + Z2) mn / aW ].
1.8. Рассчитываются геометрические параметры зубчатой передачи
Делительный диаметр шестерни d1 = mn · Z1 / cos β.
Делительный диаметр колеса d2 = mn · Z2 / cos β.
Диаметр вершин шестерни da1 = d1 + 2 mn.
Диаметр вершин колеса da2 = d2 + 2 mn.
Диаметр впадин шестерни df 1 = d1 – 2,5 mn.
Диаметр впадин колеса df2 = d2 – 2,5 mn.
Ширина колеса b2 = Ψbd · аw.
Ширина шестерни b1 = 1,12 b2.
Коэффициент ширины шестерни Ψbd = b2 / d1.
1.9. Определяется окружная скорость на делительном диаметре зубчатых колес
V = (π · d1 · n1) / 60 000,
где n1 – частота вращения шестерни, об/мин.
1.10. Выбирается степень точности зубчатой передачи в соответствии с окружной скоростью V и рекомендациями, приведенными в таблице 5.
1.11. Уточняется значение коэффициента нагрузки Кн
Кн = Кнα · Кнβ · Кнv,
где Кнα – коэффициент, учитывающий распределение нагрузки; для
прямозубых колес Кнα = 1, для косозубых и шевронных
определяется по таблице 6;
КНβ – коэффициент, учитывающий концентрацию нагрузки,
определяется по таблице 7;
КНV – коэффициент, учитывающий динамичность приложения
нагрузки, определяется по таблице П8.
1.12. Производится проверочный расчет контактных напряжений на рабочих поверхностях зубьев
σ Н=Zε{4,35·Е1·Е2·cosβ·М2·КНα·КНβ·КНv(u+1)/(Е1+Е2)·d22·b2}1/2≤[ σ Н],
где Zε – коэффициент, учитывающий суммарную длину контактных линий; для прямозубых колес при α = 20º, Zε = 0,9 для косозубых и шевронных Zε = 0,8.
Если полученное в результате расчета контактное напряжение меньше или превышает допускаемое напряжение [σ Н ] не более, чем на 3%, т.е.
Е = (σ Н - [σ Н ])/ [σ Н ] · 100% < 3%,
то прочность зубчатой передачи по контактным напряжениям считается обеспеченной.
Если же Е > 3%, то необходимо увеличить аW, или подобрать для изготовления зубчатых колес материал, обеспечивающий более высокое значение [σ Н ]. В зависимости от принятого решения производятся вновь необходимые расчеты в соответствии с данной методикой.
1.13. Определяются силы, действующие в зацеплении зубчатых колес
Окружная сила Ft = 2 М2 / d2.
Радиальная сила Fr = Ft · tgα / cos β.
Осевая сила Fa = Ft · tg β.
1.14 Производится проверочный расчет зубьев по напряжениям изгиба
σ F = (YF · Yβ · Ft · Кα · КF β · КF v)/ b2 · mn ≤ [σ F ]
где YF – коэффициент формы зуба; принимается по таблице П9 в
зависимости от эквивалентного числа зубьев ZV,
определяемого ZV = Z / cos³ β;
Yβ - коэффициент наклона зуба, определяемый Yβ = 1- β /140;
КFα – коэффициент распределения нагрузки; для прямозубых
передач КFα = 1, для косозубых и шевронных передач
значения КFα принимаются по таблице 10;
КFβ – коэффициент концентрации нагрузки; принимается по
таблице 11;
КFv - коэффициент динамичности нагрузки; принимается по
таблице 12.
Расчет ведется для зубьев того из колес, для которого отношение (σ F / YF) меньше.
Если полученное в результате расчета напряжение изгиба меньше или превышает допускаемое напряжение не более, чем на 3%, т.е.
Е= {σF - [σF]}/[σF] ·100% < 3%,
прочность зубьев на изгиб считается обеспеченной.
Если же Е > 3%, то необходимо увеличить mn или b2, или подобрать для изготовления зубчатых колес материал, обеспечивающий более высокое значение [σ F ]. В зависимости от принятого решения производятся вновь необходимые расчеты в соответствии с данной методикой.
1.15. В ряде случаев σ F оказывается значительно меньше [σ F ]. В этих случаях недогруженность передачи по напряжениям изгиба позволяет уменьшить значение mn без изменения аW и увеличить соответственно Z1 и Z2. Увеличение Z1 и Z2 без изменения аw благоприятно сказывается на работе передачи ― уменьшаются погрешности в зацеплении при той же степени точности изготовления колес, снижается интенсивность шума и виброактивность, снижаются потери на трение.
Расчет по обеспечению большей равнопрочности зубьев по контактным напряжениям изгиба проводится в следующей последовательности.
1.15.1. Уменьшается стандартное значение mn по таблице 3.
1.15.2. Определяется суммарное число зубьев передачи
ZΣ = Z1+Z2, ZΣ = 2 аw · cos β / mn.
1.15.3. Определяются числа зубьев шестерни и колеса
Z1 = ZΣ / (i12 + 1), Z2 = Z1 · i12.
Значения Z1 и Z2 округляют до целых.
1.15.4. Определяется уточненное передаточное число u = Z2 /Z1.
1.15.5. Повторяются расчеты по пунктам 1.6 ― 1.14.
2. ПРИМЕР РАСЧЕТА ПЕРЕДАЧИ.
Необходимо выполнить расчет закрытой косозубой цилиндрической передачи. Исходные данные:
Частота вращения шестерни n1 = 1500 об/мин.
Требуемое передаточное отношение передачи i12 = 3,55.
Крутящий момент на валу шестерни М1 = 19100 Н·мм.
Крутящий момент на валу колеса М2 = 65770 Н·мм.
Передача нереверсивная. Режим нагрузки постоянный.
Срок службы L = 5 лет.
Коэффициент использования передачи в году Кгод = 0,8; в сутках Ксут = 0,5.
Шестерня и колесо расположены несимметрично относительно опор.
2.1. Расчет выполняется вручную.
2.1.1. Выбираем материал для изготовления шестерни и колеса. Так как заданием не предусматривается специальных требований к габаритам и массе передачи, по таблице 1 выбираем в качестве материалов для изготовления зубчатых колес стали со средними механическими характеристиками и относительно невысокой стоимостью. Для шестерни – 40Х, термообработка – улучшение НВ 245, σ н lim b1 = 560 МПа, Sн1 = 1,1; σ0 F lim b2 = 440 МПа, SF1 = 1,6; для колеса – сталь 45, термообработка – нормализация НВ=190, σ н lim b2 = 455 МПа, Sн2 = 1,1; σ 0 F lim b2 = 350 МПа, SF2 = 1,65.
2.1.2. Рассчитываем допускаемые напряжения с учетом фактических условий нагружения.
Базовое число циклов напряжений
NHO1 = 30 НВ2,4 = 30 · 2452,4 = 1,6 · 107;
NHO2 = 30 · 1902,4 = 8,8 · 106;
NFO1 = NFO2 = 4 · 106
Время работы передачи за весь срок службы
tΣ = L · 365 · Кгод · 24 · Ксут = 5 · 365 · 0,8 · 24 · 0,5 = 17520 часов
Число циклов напряжений
NHE1 = NFE1 = 60 · n1 · tΣ = 60 · 1500 · 17520 = 1,58 · 109
NHE2 = NFE2 = 60 · n1 · tΣ / i1,2 =60 · 1500 · 17520 / 3,55 = 4,45 · 108
Коэффициенты долговечности KHL1 = KHL2 =1, так как NHE1 > NHO1 и
NHE2 > NHO2; KFL1 = KFL2 =1, так как NFE1 > NFO1 и NFE2 > NFO2.
Коэффициенты KFC1 = KFC2 =1, для нереверсивной передачи.
Допускаемые контактные напряжения
[σн]1= (σн lim b1 / SH1) · KHL1 = (560 / 1,1) · 1= 509 МПа,
[σн]2= (σн lim b2 / SH2) · KHL2 = (455 / 1,1) · 1= 414 МПа.
Допускаемые напряжения при изгибе
[σF]1= (σ 0F lim b1 / SF1) · KFC1 · KFL1 = (440/ 1,6) · 1 · 1= 275 МПа,
[σF]2= (σ0F lim b2 / SF2) · KFC2 · KFL2 = (350/ 1,65) · 1 · 1= 212 МПа.
2.1.3. Определяем числа зубьев шестерни колеса и передаточное число.
Принимаем угол наклона линии зуба β = 11º.
Число зубьев шестерни по условию неподрезания Z1 >17cos³ β =17cos³11º=16,08.
Принимаем Z1 = 16.
Число зубьев колеса Z2 = Z1 · i12 = 16 · 3,55 = 56,8 принимаем Z2 = 57.
Передаточное число u = Z2 / Z1 = 57/16 = 3,56.
Относительное расхождение между передаточным числом и требуемым передаточным отношением
(u - i12)/ i12 · 100% = (3,56 – 3,55)/3,55 · 100% = 0,35%,
что допустимо.
2.1.4. Определяем требуемое межосевое расстояние передачи из условия контактной прочности.
аW = (u +1){0,78· М2 · КН ·cos β · Е1 · Е2 / ([σ Н ]· u)²· Ψbа ·(Е1 + Е2)}1/3 =
= (3,56+1){0,78·65770·1,2·cos11º·2,1·105·2,1·105/(414·3,56)²·0,25·(2,1+2,1)·105 = 103,47мм.
Коэффициент нагрузки предварительно принимаем КH = 1,2;
Е1 = Е2 = 2,1·105 Мпа (см. таблица 1).
Расчетное допускаемое напряжение
[σ Н ] = [σ Н ] min = [σ Н ] 2 = 414 МПа.
Коэффициент Ψba с учетом твёрдости ≤ НВ 350 и несимметричного расположения колес относительно опор по таблице 2 принимаем Ψba = 0,250.
2.1.5. Определяем модуль передачи
mn = (2 · aw · cos β)/(Z1 + Z2) = 2 ·03,47 ·cos11º (16+57) = 2,78 мм.
По таблице 3 принимаем стандартное значение модуля mn = 2,75 мм.
2.1.6. Уточняем межосевое расстояние передачи
аw = 0,5(Z1 + Z2) mn /cos β = 0,5(16+57) 2,75/cos11º = 102,25 мм.
За уточненное значение принимаем целую часть аw = 102 мм.
2.1.7. Уточняем угол наклона линии зуба
β =arccos[0,5(Z1 + Z2) mn / аw ]=arccos0,5(16+57)2,75/102=10,241º =10º14´29″.
2.1.8 Рассчитываем геометрические параметры зубчатой передачи.
Делительные параметры
d1 = mn · Z1 / cos β = 2,75 · 16 / cos 10º14´29″ = 44,712 мм;
d2 = mn · Z2 / cos β = 2,75 · 57 / cos 10º14´29″ = 159,288 мм.
Диаметры вершин
da1 = d1 + 2· mn = 44,712 + 2· 2,75 = 50,212 мм;
da2 = d2 + 2· mn = 159,288 + 2 · 2,75 = 164,788 мм.
Диаметры впадин
df1 = d1 - 2,5 · mn = 44,712 – 2,5 · 2,75 = 37,837 мм;
df2 = d2 - 2,5 · mn = 159,288 – 2,5 · 2,75 = 152,413 мм.
Ширина колеса b2 = Ψba · аw = 0,25 · 102 = 25,5 мм, принимаем b2 = 25мм.
Ширина шестерни b1 = 1,12 · b2 = 28 мм.
Коэффициент ширины шестерни Ψbd = b2 / d1 = 25 / 44,712 = 0,56.
2.1.9. Определяем окружную скорость на делительном диаметре зубчатых колес
v = (π · d1 · n1)/60 000 = (π·44,712·1500)/60 000 = 3,61 м/с.
2.1.10. Принимаем с учетом рекомендаций, приведенных в таблицах 5,8 степень точности передачи.
2.1.11. Уточняем значения коэффициентов нагрузки
КHα = 1,09 – по таблице П6;
КHβ = 1,06 – по таблице П7;
КHv = 1,04 – по таблице П8.
2.1.12. Производим проверочный расчет контактных напряжений на рабочих поверхностях зубьев
σн = Zε {4,35· Е1 · Е2 ·cos β · М2 · КНα · КНβ · КНv (u +1)/(Е1 + Е2)· d2 · b2 }1/2 =
=0,8{4,35·(2,1·105)2·cos10º14´·65770·1,08·1,06·1,04(3,56+1)/(2,1+2,1)·105·(159,288)²·25=
= 401,47 МПа ≤ [σ Н ] = 414 МПа.
Zε = 0,8 - коэффициент, учитывающий суммарную длину контактных линий,
для косозубых колес при α = 20º.
2.1.13. Определяются силы, действующие в зацеплении зубчатых колес
Окружная сила
Ft = 2 · М2 / d2 = 2 · 65770 / 159,288 = 825,79 Н.
Радиальная сила
Fr = Ft · tg 20º/cos β. = 825,79 · tg 20º / cos 10º14´29″ = 305,42 Н.
Осевая сила
Fa = Ft tg β = 825,79 tg 10º14´29″ = 149,19 H.
2.1.14. Определяем коэффициенты формы зубьев шестерни YF1 и колеса YF2
YF1 = 4,28 по таблице 9 для ZV1 = Z1 · cos³ β = 16 / cos³ 10º14´29″ = 15,2;
YF2 = 3,65 по таблице 9 для ZV2 = Z2 · cos³ β = 57 / cos³ 10º14´29″ = 54,3.
2.1.15. Определяем коэффициент наклона зуба
Yβ = 1- β / 140 = 1 – 10,24138/140 = 0,926.
2.1.16. Определяем коэффициенты нагрузки для расчета напряжений изгиба зубьев КFα = 0,91 – таблице 10;
КFβ = 1,12 – таблице 11;
КFv = 1,11 – таблице 12.
2.1.17. Определяем отношения [σ F ]/ YF
[ σ F ] 1 / YF1 = 275 / 4,28 = 64,25 МПа;
[ σ F ] 2 / YF2 = 212 / 3,65 = 58,08 МПа.
2.1.18. Производим проверочный расчет напряжений изгиба в опасном сечении зубьев колеса, т.к. должно быть {[σ F ] 2 / YF2 }< {[σ F ] 1 / YF1 }
σ А = (НА2 · Нβ · Ае · КАα · КАβ · КАм).(и2 · ьт) =
=(3,65·0,926·825,19·0,91·1,12·1,11)/(25·2,75) = 45,89 МПа;
σ F = 45,89 МПа < [σ F ] 2 = 212 МПа.
2.1.19. С целью обеспечения большей равнопрочности передачи и увеличения Z1 и Z2 уменьшаем mn при том же значении аw.
Принимаем по таблице 3 стандартное значение mn = 1,5 мм.
2.1.20. Определяем суммарное число зубьев ZΣ = Z1 + Z2
ZΣ = 2 · аW · cos β / mn = 2 · 102 · cos 10º14´29″ / 1,5 = 133,8.
2.1.21. Определяем числа зубьев шестерни и колеса
Z1 = ZΣ / (i12 +1) = 133,8 / 3,55 + 1 = 29,4 принимаем Z1 = 29.
Z2 = Z1 · i12 = 29 · 3,55 = 102,95 принимаем Z2 = 103.
2.1.22. Определяем передаточное число
u = Z1 / Z2 = 103 / 29 = 3,5517.
Относительное расхождение между u и i12 очень мало.
2.1.23. Уточняем угол наклона линии зуба
β = arccos [ 0,5 (Z1 + Z2) mn / аW ] =
= arcos [ 0,5 (29 + 103) · 1,5 / 102 ] = 13,93055º = 13º55′50″.
2.1.24. Рассчитываем геометрические параметры зубчатой передачи
d1 = mn · Z1 / cos β = 1,5 · 29 / cos 13º55′50″ = 44,818 мм;
d2 = mn · Z2 / cos β = 1,5 · 103 / cos 13º55′50″ = 159,182 мм;
da1 = d1 + 2 · mn = 44,818 + 2 · 1,5 = 47,818 мм;
da2 = d2 + 2 · mn =159,182 + 2 · 1,5 = 162,182 мм;
df1 = d1 – 2,5 · mn = 44,818 – 2,5 · 1,5 = 41,068;
df2 = d2 – 2,5 · mn = 159,182 – 2,5 · 1,5 = 155,432 мм;
b2 = 25мм. b1 = 28мм Ψbd = 0,62.
2.1.25. Повторяем проверочный расчет контактных напряжений
σ Н =0,8{[4,35·2,1·105·2,1·105cos13º55´·65770·1,09·1,06]/[(2,1+2,1)105·(159,182)²·25]}1/2=
= {1,04(3,55+1)}1/2 = 401,39 МПа < [σ Н ] = 414 МПа.
2.1.26. Определяем силы в зацеплении
Ft = 2 · М2 / d2 = 2 · 65770 / 159,182 = 826,35 Н;
Fr = Ft · tg α / cos β = 826,34 · tg 20º / cos 13º55´50″ = 309,88 Н;
Аф = Ае · епβ = 826б34 · еп 13º55´50″ = 204б97 Ню
2.1.27. Определяем коэффициенты зубьев YF1 и YF2
YF1 = 3,90 ZV1 = Z1 cos3 β = 29 cos313º55´50″ = 26,5;
YF2 = 3,60 ZV2 = Z2 cos3 β = 103 cos3 13º55´50″ = 94,1.
2.1.28. Определяем коэффициент наклона зуба
Yβ = 1- β /140 = 1 – 13,93055 / 140 = 0,90.
2.1.29. Определяем коэффициенты нагрузки
КFα = 0,91; КFβ = 1,12; КFV =1,11.
2.1.30. Определяем отношения
[σ F ] 1 / YF1 = 275 / 3,90 = 70,51 МПа;
[σ F ] 2 / YF2 = 212 / 3,60 = 58,88 МПа.
2.1.31. Повторяем проверочный расчет напряжений изгиба в опасном сечении зубьев колеса, т.к.
σ F = (3,60·0,90·826,34·0,91·1,12·1,11)/(25·1,5) = 80,82 МПа.
Сравниваем полученное значение с допускаемым напряжением изгиба
σ F = 80,82 МПа < [σ F ] 2 = 212 МПа
и видим, что условие прочности на изгиб выполняется, что даёт нам основание считать выполненные расчёты верными.
ЛИТЕРАТУРА
1. Трухман В.М., Фёдоров В.В.. Янковский В.В. Расчёт закрытых цилиндрических передач на ЭВМ: Методические указания для студентов.– Куйбышев: КИИТ, 1985.
2. Беляков В.М., Жарков М.С., Фёдоров В.В., Янковский В.В. Зубчатые передачи подвижного состава: Учебное пособие для студентов. Куйбышев.: КИИТ, 1990.
3. Иванов М.Н. Детали машин.– М.: Высшая школа, 1991.
4. Курсовое проектирование деталей машин: Учебное пособие для учащихся машиностроительных специальностей/ Под ред. Чернавского С.А.– М.: Машиностроение, 1988.
5. Зубчатые передачи: Справочник/ Под ред.Е.Г.Гинзбурга.-Л.:Машиностроение,1984.- 400 с.
6. Проектирование механических передач: Учебное пособие для машиностроительных техникумов/ Под ред. Чернавского С.А.– М.: Машиностроение, 1984.
7. Курсовое проектирование деталей машин: Учебное пособие для вузов/ Под ред. Ицковича Г.М.– М.: Высшая школа, 1989.
8. Биргер И.А., Шорр Б.Ф., Иосилевич Г.Б. Расчёты на прочность деталей машин.– М.: Машиностроение, 1979.
9. Толстоногов А.А. Детали машин и основы конструирования: конспект лекций.- СамГАПС. 2003.
ПРИЛОЖЕНИЕ
 |
















