Линейная регрессионная модель

Расчетно-графическая работа

по дисциплине «Эконометрика»

ДВУМЕРНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ

Исполнитель___________________ Баянова Д.В. группа МРК-07-2

дата, подпись

Руководитель __________________ к.э.н., доцент Ежова Л.Н.

Иркутск, 2009

Линейная регрессионная модель

(В. № 11)

Распределение автопредприятий по числу рабочих (x) и перевозок (y):

Х_i – число рабочих, чел. – объясняющая переменная, фактор.

Y_i – объем перевозок, млн.руб. - результирующая переменная.

n=10

Число рабочих-X (чел)
Объем перевозок – Y (млн.руб.)

1) Для построения диаграммы рассеивания нанесем на координатную плоскость XOY точки , . Т.к. точки на диаграмме рассеивания разбросаны относительно прямой, есть основание считать, что связь между x и y линейна и описывается уравнением.

Рисунок 1

2) Связь между х и у описывается уравнением y=a+bx, где a и b – неизвестные параметры.

Результаты наблюдений и необходимые расчеты

для построения линейной регрессии




№	х_i	y_i	x_i²	y_i²	x_iy_i	ŷ_i	y_i-ŷ_i	(y_i-ŷ_i)²
						49,79	0,2022	0,04080
						51,87	-1,8797	3,5332
						51,87	-1,8797	3,5332
						51,87	-1,8797	3,5332
						62,28	-2,2892	5,2404
						62,28	-2,2892	5,2404
						62,28	7,7108	59,4564
						62,28	7,7108	59,4564
						72,69	-2,6987	7,2829
						72,69	-2,6987	7,2829
∑						599,99	0,0089	154,6004
Сред.	28,9		850,1			59,99	0,0008	15,6004

Оценки этих параметров, найдем методом наименьших квадратов

– система нормальных уравнений

Используя итоги столбцов (2 – 6), найдем оценки коэффициентов регрессии:

= - 0,1678

2,0819

Тогда уравнением линейной регрессии будет:

ŷ= - 0,1678 + 2,0819x

Оценка дисперсии случайной составляющей:

σ² = = = 19.325

Несмещенные оценки дисперсий оценок 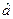и получаются в виде:

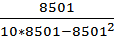= * 19.325 = 0,0023

= 0,0479

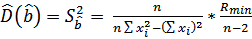= * 19.325 = 2,6772

= 1,6362

и дают оценку точности для этих коэффициентов при переносе результатов модели ŷ= с выборки на генеральную совокупность.

Интервальные оценки параметров модели определяют по формулам:

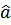- < a < +

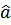- < b < + ,

где квантиль распределения Стьюдента (t – распределения) уровня и числа степеней свободы . Здесь – доверительная вероятность или надежность, . Из таблицы квантилей распределения Стьюдента найдем = t 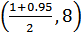=2,306

Тогда:

-0,1678 – 2,306*0,0479 < < -0,1678 + 2,306*0,0479

-0.2782 < < -0,0573

2,0819 – 2,306*1,6362 < b < 2,0819 + 2,306*1,6362

-1,6911 < b < 5,8549

ŷ= - 0,1678 + 2,0819x

(0.0479) (1.6362)

3) Оценка значимости коэффициентов регрессии проводится с целью установления несущественных факторов: фактор, коэффициент при котором в уравнении линейной регрессии статистически незначим, оказывает несущественное влияние и должен быть исключен из модели.

Проверяемые гипотезы:

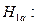
при

Проверка таких гипотез может осуществляться двумя равноценными способами: по t – критерию Стьюдента и с использованием доверительных интервалов.

I. Проверим гипотезу H_0a: a=0 при H_1a: a 0

Здесь мы рассматриваем двустороннюю критическую область, так как

H_1a:a 0.

Используем статистику t = = t (n-2), распределенную по закону Стьюдента с (n-2) степенями свободы.

= =-3,5031

Критическая точка для 5% уровня значимости и числа степеней свободы n-2=8

равна 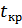=2,306

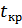< ð гипотезу H₀_a о статистической незначимости коэффициента а следует принять т.е. считать, что результаты наблюдений согласуются с гипотезой H_0,не противоречат ей.

II. Проверим гипотезу Н_0b: b = 0 при

Используем статистику t = = t (n-2), распределенную по закону Стьюдента с (n-2) степенями свободы.

= = 1,27

Критическая точка для 5% уровня значимости и числа степеней свободы n-2=8

равна 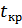=2,306

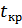< ð гипотезу Н_0b о статистической незначимости коэффициента b следует принять, т.е. считать, что результаты наблюдений согласуются с гипотезой H_0,не противоречат ей.

Проверку гипотез H₀ можно провести и с использованием построенных доверительных интервалов для параметров модели: интервальные оценки этих параметров есть области принятия нулевых гипотез. Так как интервальные оценки теоретических коэффициентов регрессии не содержат гипотетических значений, равных 0, то гипотезы H₀ в том и в другом случаях следует отвергнуть.

4) Дисперсионный анализ регрессии.

Для этого составим вначале вспомогательную расчетную таблицу

Расчет сумм квадратов

№
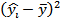
	49,79	-10	-10,21	0,2022	104,24	0,04080
	51,87	-10	-8,13	-1,8797	66,09	3,5332
	51,87	-10	-8,13	-1,8797	66,09	3,5332
	51,87	-10	-8,13	-1,8797	66,09	3,5332
	62,28		2,28	-2,2892	5,19	5,2404
	62,28		2,28	-2,2892	5,19	5,2404
	62,28		2,28	7,7108	5,19	59,4564
	62,28		2,28	7,7108	5,19	59,4564
	72,69		12,69	-2,6987	161,13	7,2829
	72,69		12,69	-2,6987	161,03	7,2829
Итог	599,9		-0,1	0,0089	645,40	154,6

= = * 600 = 60

SS_общ =∑ = 800

SS_R =∑ = 645,4

SS _ост =∑ (y_i- ŷ _i)²= 154,6

800 ≈ 645,4 + 154,6 (знак приближенного равенства из-за погрешностей округления).

Дисперсионный анализ парной регрессии

Источник дисперсии	Число степеней свободы	Сумма квадратов SS	Средний квадрат MS	Критерий Фишера F	Критическая точка	Гипотеза
Регрессор х		645,4	645,4	33,44	F(0,05; 1, 8)=5.32	H₀: b≠0
Ошибка (остаток)		154,6	19,3	-	-	-
Общая дисперсия (итог)			-	-	-	-

Гипотеза об отсутствии линейной функциональной связи эквивалентна гипотезе о равенстве дисперсий, обусловленных регрессором х и ошибкой наблюдений . Если эти дисперсии различаются между собой случайно, то есть незначимо, то фактор или регрессор х оказывает несущественное влияние и следует принять. Для проверки гипотезы о равенстве дисперсий используется критерий, статистика которого распределена по закону Фишера с соответствующими числами степеней свободы. Если гипотеза отвергается.

В нашем примере F = 33.44, F₀ =(0,05; 1, 8).

33,44 > 5,32 ð гипотезу следует отвергнуть и считать, что результаты наблюдений не противоречат предположению о линейной связи между х и y, уравнение регрессии достаточно качественно отражает динамику изменения зависимой переменной Y.

Коэффициент детерминации R²= SS_R/SS_общ=0,8067 показывает, что 80,67% общей дисперсии объема перевозок объясняется количеством рабочих, в то время как на все остальные факторы приходится 19,32% изменчивости объема перевозок.

Найдем коэффициент корреляции:

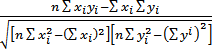= = = ≈ 0,8981

R²=r²=0,806. Высокое значение как коэффициента корреляции, так и коэффициента детерминации свидетельствует о том, что данные наблюдений хорошо согласуются с представлением их в виде линейной регрессионной модели.

5) Дадим интерпретацию коэффициентам регрессии. Если не учитывать, что мы имеем не теоретическую, а эмпирическую линию регрессии, то коэффициент

= 2,0819 показывает, что увеличение числа рабочих на одного человека приводит к увеличению объема перевозок на 208,19 млн.руб. Это своего рода эмпирический норматив приростной эффективности использования работников на данном предприятии. Если увеличение численности на одного работника приводит к меньшему росту объема перевозок, то прием его на работу необоснован.

Отрицательное значение коэффициента 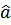= -0,1678 означает, что если мы рассмотрим предприятие без работников, то объем перевозок будет снижаться, это вполне логично, хотя ситуация может показаться парадоксальной. Константа определяет положение линии регрессии на графике.

Далее посчитаем эластичность

= * = 2,0819 * 28,9/60 = 1,002. Это значит, что изменение количества работников сильно повлияет на изменение объема перевозок.

6) Полученное уравнение регрессии может быть использовано для прогноза. В частности, пусть количество рабочих будет 40 человек. Тогда достаточно обоснованный объем перевозок следует установить по уравнению регрессии:

= - 0,1678 + 2,0819*40 = 83,1082 млн.руб.

Доверительный интервал с надежностью = 0,95, для теоретического значения прогноза определим по формулам:

= = = 19.325

83.1082-10,13*0.0393*0,96 < y₀< 83.1082+10,13*0.0393*0,96

82,72 < y₀< 83,49

То есть мы на 95 % уверены в том, что объем перевозок для предприятия с численностью 40 чел. будет в указанных пределах.