деформаций (скоростями деформаций)
Возвратимся к гипотезе о коаксиальности (совпадении главных направлений) тензоров 
и 
( и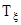 
) и к гипотезе о подобии девиаторов 
и 
( и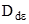 
) для изотропного материала.
В силу условия (3.1)
= 
= 
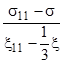имеем
(3.1 а)
Аналогичное соотношение можно записать для девиатора приращений деформации
(3.1 б)
Коэффициент пропорциональности 
- бесконечно большая величина, так как 
- бесконечно малые величины, а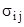 
- конечные напряжения.
Ограничемся в начале случаем (3.1 б), свойственным процессу холодной деформации. Если перейти в правой и левой части от базиса, совпадающего с направлениями главных нормальных напряжений к произвольному базису 
, то условие коаксиальности и подобия девиаторов примет вид
или
(3.4)
Подставив значение 
в формулу интенсивности касательных напряжений
получим
Откуда
Если сейчас подставить значения в формулу (3.4), то получим уравнение связи и 
, справедливые для любой изотропной среды
(3.5)
Если нам дана единая кривая упрочнения металла в холодном состоянии (3.2) Т= Т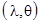 
, то уравнения (3.4) примут вид
(3.6)
При развитой пластической деформации можно пренебречь упругой частью компонентов девиатора приращения деформации связанной с изменением объема, тогда получим
, (3.6 а)
где
, так как 
Действительно, если известно деформированное состояние и кривая упрочнения
Т= Т 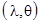, то по этим формулам можно подсчитать компоненты девиатора напряжения.
Аналогично для задач, решаемых в скоростях, будет
(3.7)
или
(3.8)
Для несжимаемых материалов эти формулы будут проще
(3.8 а)
где 
, так как 
В этих формулах значение Т полагаем заданным уравнением (3.3)
