Dr
D j
XMAX
максимум
2_9. ƒ»‘–ј ÷»ќЌЌјя –≈Ў≈“ ј
ќзнакомьтесь с теорией в конспекте, учебнике (—авельев, т.2, І129,130). «апустите программу ЂЁл-магн. вантыї. ¬ыберите Ђќптикаї и Ђƒифракционна€ решеткаї. Ќажмите вверху внутреннего окна кнопку с изображением страницы. ѕрочитайте краткие теоретические сведени€. Ќеобходимое запишите в свой конспект. (≈сли вы забыли, как работать с системой компьютерного моделировани€, прочитайте ¬¬≈ƒ≈Ќ»≈ стр.5 еще раз).
÷≈Ћ№ –јЅќ“џ:
* «накомство с моделированием процесса сложени€ когерентных электромагнитных волн.
* Ёкспериментальное исследование закономерностей взаимодействи€ световых волн с периодической структурой (дифракционной решеткой).
–ј“ јя “≈ќ–»я:
«арисуйте с экрана компьютера то, что расположено в трех пр€моугольных рамках.
ƒ»‘–ј ÷»ќЌЌќ… –≈Ў≈“ ќ… называетс€ совокупность большого числа N одинаковых, отсто€щих друг от друга на одно и то же рассто€ние, пр€моугольных щелей в плоском непрозрачном экране.
ѕ≈–»ќƒќћ (посто€нной) дифракционной решетки называетс€ рассто€ние d между серединами соседних щелей или сумма ширины щели b и ширины непрозрачного участка a.
ѕри анализе излучени€, проход€щего через решетку, обычно используют линзу и экран, расположенный в фокальной плоскости линзы на рассто€нии L от нее. Ћинза собирает параллельные лучи в одну точку на экране. ѕоложение ’ точки на экране зависит от угла падени€ q лучей на линзу: X = Lsin(q). ƒл€ очень малых углов sin(q) = q и X = qL.
–ј«Ќќ—“№ ’ќƒј лучей от соседних щелей D = dsin(q).
–ј«Ќќ—“№ ‘ј« лучей от соседних щелей  .
.
»Ќ“≈Ќ—»¬Ќќ—“№ »«Ћ”„≈Ќ»я, идущего от решетки под углом q:
I–≈Ў = I0  ,
,
где I0 - интенсивность, создаваема€ одной щелью против центра линзы, b - ширина щели. ѕервый множитель обращаетс€ в 0 в точках, дл€ которых bsin(qk) = ±kl (k = 1,2,...). ¬торой множитель принимает значение N2 в точках, удовлетвор€ющих условию dsin(qm) = ±ml (m = 0,1,2,...). ѕоследнее условие определ€ет положение √Ћј¬Ќџ’ ћј —»ћ”ћќ¬ излучени€, а m называетс€ пор€дком максимума. »нтенсивность в главном максимуме преобразуем, раскладыва€ синус в р€д и ограничива€сь первыми двум€ членами разложени€:
Im = N2I0  .
.
ќбозначим  .
.
ќтношение Rm интенсивности в m-том максимуме к интенсивности в нулевом максимуме называетс€ Ђотносительной интенсивностью m-того максимумаї.
‘ормулу  можно проверить экспериментально и из соответствующего графика получить ширину щели.
можно проверить экспериментально и из соответствующего графика получить ширину щели.
ЋјЅќ–ј“ќ–Ќјя –јЅќ“ј є 3_1
¬Ќ≈ЎЌ»… ‘ќ“ќЁ‘‘≈ “
ќзнакомьтесь с конспектом лекций и учебником (—авельев, т.3, І9). «апустите программу ЂЁл-магн. вантыї. ¬ыберите Ђ вантова€ физикаї и Ђ‘отоэффектї. Ќажмите вверху внутреннего окна кнопку с изображением страницы. ѕрочитайте краткие теоретические сведени€. Ќеобходимое запишите в свой конспект. (≈сли вы забыли, как работать с системой компьютерного моделировани€, прочитайте ¬¬≈ƒ≈Ќ»≈ стр.5 еще раз).
÷≈Ћ№ –јЅќ“џ:
* «накомство с квантовой моделью внешнего фотоэффекта.
|
|
|
* Ёкспериментальное подтверждение закономерностей внешнего фотоэффекта.
* Ёкспериментальное определение красной границы фотоэффекта, работы выхода фотокатода и посто€нной ѕланка.
–ј“ јя “≈ќ–»я:
‘отоны это частицы (кванты), поток которых €вл€етс€ одной из моделей электромагнитного излучени€ (Ёћ»).
ЁЌ≈–√»я ‘ќ“ќЌј ≈‘ = hn,
- частота излучени€, h - посто€нна€ ѕланка, h = 6.6210-34 ƒжс).
Ёнерги€ часто измер€етс€ во внесистемных единицах Ђэлектрон-вольтахї.
1 э¬ = 1.6Ј10-19 ƒж.
ћасса фотона св€зана с его энергией соотношением Ёйнштейна
≈‘ = m‘c2, отсюда m‘ = 
»ћѕ”Ћ№— ‘ќ“ќЌј p = m‘ c =  где l - длина волны Ёћ».
где l - длина волны Ёћ».
¬Ќ≈ЎЌ»… ‘отоэффект есть €вление вылета электронов из вещества (металла, фотокатода) при его облучении электромагнитным излучением (Ёћ»), например, светом. ¬ылетевшие электроны называютс€ фотоэлектронами. ƒалее дл€ краткости указанное €вление будем называть просто фотоэффектом.
инетическа€ энерги€ электрона внутри вещества увеличиваетс€ на h, но при вылете фотоэлектрона из вещества им совершаетс€ работа ј¬џ’ (работа выхода) против сил электростатического прит€жени€ к металлу. ” фотоэлектрона сообщенна€ ему фотоном порци€ энергии уменьшаетс€ на величину, равную работе выхода из металла (фотокатода), а оставша€с€ часть имеет вид кинетической энергии фотоэлектрона вне металла (фотокатода):
 = h - ј¬џ’.
= h - ј¬џ’.
Ёто соотношение называют формулой (законом) Ёйнштейна дл€ фотоэффекта.
расна€ граница фотоэффекта есть минимальна€ частота Ёћ», при которой еще наблюдаетс€ фотоэффект, т.е. дл€ которой энерги€ фотона равна работе выхода h –= ј¬џ’.
«апирающим (задерживающим) напр€жением называетс€ минимальное тормоз€щее напр€жение между анодом вакуумной лампы (фотоэлемента) и фотокатодом, при котором отсутствует ток в цепи этой лампы, т.е. фотоэлектроны не долетают до анода. ѕри таком напр€жении кинетическа€ энерги€ электронов у катода равна потенциальной энергии электронов у анода, откуда следует выражение:
U«јѕ = 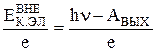 ,
,
где е - зар€д электрона.
ЋјЅќ–ј“ќ–Ќјя –јЅќ“ј є 3_2






