На рисунке показан результат графической обработки численно полученной зависимости скорости падения тела от времени при некотором наборе параметров m, k1 и k2.
Зависимость скорости падения от времени с учетом сопротивления воздуха.
Зависимость не имеет ничего общего с линейным изменением скорости, которое получается без учета сопротивления воздуха. Выход скорости на постоянное значение происходит в процессе приближения силы сопротивления воздуха к силе тяжести. При их равенстве движение становится равномерным.
Заметим, что установившееся предельное значение скорости можно вычислить аналитически, не прибегая к численным методам. Приравняв в формуле (6) dv/dt (ускорение) к нулю, получим, что установившаяся скорость будет равна
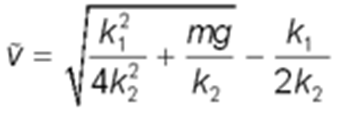
и далее не будет возрастать.
На основании данной модели можно, например, решать задачу оптимизации, сформулировав условие так: парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость? Другая задача: как связана высота прыжка с площадью поперечного сечения парашюта (входящей в k2), чтобы скорость приземления была безопасной?
Существенной проблемой при использовании описанного численного метода является выбор величины шага по времени t. От этой величины зависит точность получаемых результатов, устойчивость вычислительной процедуры. Все эти проблемы исследуются в математической дисциплине, которая называется “Численные методы”, или “Вычислительная математика”.
Численные методы — это методы, сводящие решение любой математической задачи к арифметическим вычислениям. Покажем применение численного метода решения на примере более простой задачи механики, чем задача о полете ракеты. Рассмотрим задачу о свободном падении тела постоянной массы m под действием постоянной силы тяжести. Уравнения движения с учетом сопротивления воздуха (об этом говорилось выше) имеют вид:
(6),(7)
Здесь v — вертикальная составляющая вектора скорости. Пусть начальная высота тела над землей равна s0, а начальная скорость — v0.
Покажем применение метода, который называется методом Эйлера, к расчету движения падающего тела. Расчет производится от начального момента времени t = 0 с малым конечным шагом по времени t. За время t скорость изменится на величину v.
На основании определения производной заменим в уравнении (6) производную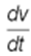 
на приближенное к ней отношение v/t. Зная скорость v0 в начальный момент времени t = 0 и обозначив через v1 ее значение в момент t, перепишем уравнение (6) в виде:
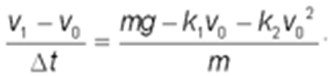
Отсюда получим формулу для вычисления v1:
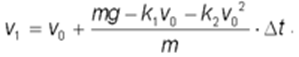
Это и есть формула метода Эйлера.
Далее рассуждение ведется по индукции. Располагая значением v1, можно, отталкиваясь от него, найти v2 — скорость в момент времени 2t и т.д. Общий вид формулы применительно к данной задаче получится таким:
(n = 0, 1, 2, …). (8)
Применяя аналогичный подход к уравнению (7), получаем формулу метода Эйлера для вычисления перемещения падающего тела со временем:
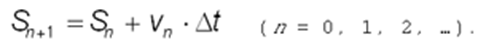
(9)
Имея начальные значения скорости и перемещения, а также используя формулы (8), (9), можно шаг за шагом вычислять значения v и s в последовательные моменты времени. Этот процесс несложно запрограммировать, а полученные результаты вывести в виде числовой таблицы и представить в графическом виде.
Литература:
1.Роберт И.В., Самойленко П.И. Информационные технологии в науке и образовании. М: Школа-Пресс, 2002
2.Беспалько В.П. Образование и обучение с участием компьютеров. М: Бином, 2005
3. Бусленко Н. П. Моделирование сложных систем. Москва, 1961.
4. Интернет источник.
5 Статья, опубликованная в № 13/2007 журнала "Информатика" издательского дома "Первое сентября".
