Основным законом механики является второй закон Ньютона, связывающий силу, действующую на тело, его массу и ускорение, получаемое в результате действия силы. В школьной физике этот закон представляется в следующем виде:
(1)
При этом подразумевается, что сила и масса — постоянные величины. В таком случае и ускорение тоже будет постоянной величиной. Следовательно, уравнение (1) моделирует равноускоренное движение тела с постоянной массой под действием постоянной силы.
Применимость такой модели ограничена. Ее нельзя использовать для расчета движения тел с переменной массой и переменной силой. Например, при полете ракеты ее масса уменьшается за счет выгорания топлива, т.е. масса является функцией времени: m(t). Вследствие этого ускорение тоже становится переменной величиной и математическая модель изменится:
Учтем, что ускорение — это производная от скорости (v) по времени, и опишем функцию изменения массы со временем (пусть она будет линейной); получим следующую математическую модель движения:
(2)
Здесь m0 — начальная масса ракеты, q (кг/с) — параметр, определяющий скорость сгорания топлива. Уравнение (2) — это дифференциальное уравнение, в отличие от линейного алгебраического уравнения (1). Математическая модель усложнилась! Решать уравнение (2) значительно сложнее, чем (1). Если же учесть еще и возможность изменения со временем силы F(t) (сила тяги ракетного двигателя в процессе запуска — переменная величина), то модель станет еще сложнее:
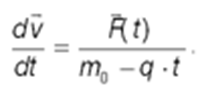
(3)
При движении тел в атмосфере (или в жидкой среде) необходимо учитывать сопротивление среды — силу трения. Сила трения имеет две составляющие: пропорциональную первой степени скорости тела и пропорциональную ее квадрату. Теперь уравнение движения примет вид:
(4),(5)
Здесь k1 и k2 — эмпирические коэффициенты. Уравнение (5) связывает скорость с перемещением. Модель (4)–(5) стала ближе к физически реальной ситуации, но сложнее с математической точки зрения. Используя ее, можно получить ответы на практически важные вопросы. Например: при заданной F(t) определить, через сколько времени и на какой высоте ракета достигнет первой космической скорости. Или решить обратную задачу: какой должна быть сила тяги двигателя для того, чтобы на заданной высоте ракета достигла первой космической скорости? Если учитывать еще тот факт, что коэффициенты k1 и k2 — переменные величины, поскольку они зависят от плотности атмосферного воздуха, которая уменьшается с высотой, математическая модель (4)–(5) становится достаточно сложной. Решение на основе такой модели задач, сформулированных выше, требует использования численных методов и компьютера.
