Однако графики не всех поверхностей могут быть построены с помощью задания матрицы аппликат или способом, рассмотренным в разделе 3.2. Такие поверхности существуют уже среди поверхностей второго порядка: например, эллипсоид, каноническое уравнение которого имеет вид
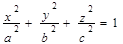 . (1)
. (1)
Невозможность построения графика поверхности упомянутыми способами объясняется следующим.
Зададим область изменения аргументов x, y:
- a £ x £ a, - b £ y £ b (2)
и выразим из (1) переменную z:
 . (3)
. (3)
Из (3) следует, что для некоторых значений x, y из области определения (2) переменная z может быть мнимой величиной. Это предопределяет невозможность построения графика с помощью задания матрицы аппликат.
Для таких поверхностей в MathCAD 2001 предусмотрен иной способ построения графиков. Но для этого необходимо перейти от явного или неявного задания поверхности к ее заданию в параметрической форме.
При параметрическом задании функции z = f (x, y) все три переменные x, y, z представляются как функции некоторых двух переменных u, v, называемых параметрами: x = x (u, v), y = y (u, v), z = z (u, v). Часто в качестве параметров u, v выбирают углы j, q, образуемые радиусом – вектором, проведенным из начала координат к некоторой точке M поверхности, и его проекцией на какую – либо координатную плоскость с осями координат. На рис 12 приведен пример выбора параметров j, q.
 |
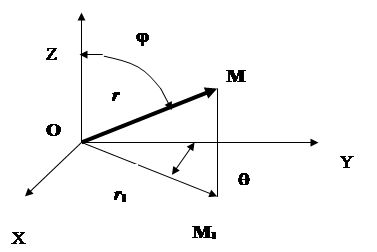
Рис.12.
Здесь: M – точка поверхности; M1 – проекция точки M на плоскость XOY; r – радиус – вектор, проведенный из начала координат в точку M; r 1 – проекция вектора r на плоскость XOY; j - угол, образованный вектором r с осью OZ; q - угол, образованный вектором r 1 с осью OY.
Подчеркнем, что рис. 12 всего лишь пример выбора параметров. Параметры u, v могли бы быть выбраны и по-иному.
Если же параметры выбраны в соответствии с рис. 12, то уравнение эллипсоида в параметрической форме имеет вид
x (j,q) = a sin (j) sin (q),
y (j,q) = b sin (j) cos (q), (4)
z (j,q) = c cos (j).
Истинность параметрического представления (4) проверяется подстановкой (4) в уравнение (1).
Для построения графика функции двух переменных (поверхности), заданной в параметрической форме, следует:
1) задать область изменения индексов i, j;
2) задать область изменения параметров в виде индексированных переменных (например, j i, q j);
3) задать поверхность в параметрической форме (например, xi , j, yi , j, zi , j);
4) набрать и выполнить команду: Insert – Graph – Surface Plot;
5) в структурную метку шаблона графика, расположенную около начала координат, ввести имена координат – (x, y, z) (без индексов и в круглых скобках).
На рис. 13 приведен фрагмент программы MathCAD 2001 по построению графика поверхности эллипсоида.
 |
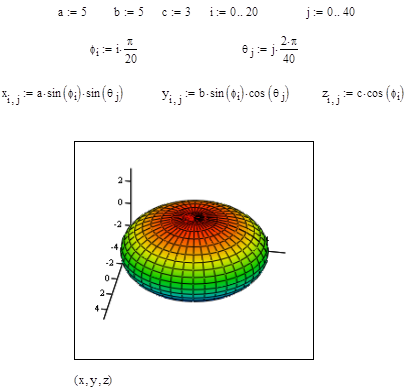
Рис. 13.
Для многих поверхностей их параметрические представления найдены и приведены в учебниках и справочниках по математике. Но не всегда во время работы за компьютером эти могут оказаться “под рукой”. Поэтому полезно уметь самостоятельно переходить от задания поверхности в виде уравнения в прямоугольных координатах к ее параметрическому заданию. При этом для большинства поверхностей второго порядка удобно в качестве параметров выбирать координату z (будем этот параметр обозначать как h) и угол q.
На примере эллипсоида (1) рассмотрим, как при выбранных параметрах h, q получаются параметрические представления большинства поверхностей второго порядка.
Положим в (1): z = h. Получим

или
 . (5)
. (5)
Уравнение (5) – это уравнение эллипса с полуосями
 и
и  .
.
Параметрическое представление эллипса известно:
x = A sin (q), y = B cos (q).
Следовательно, параметрическое представление эллипсоида при выбранных параметрах h, q:
 ,
,
 ,
,
z = h.
Фрагмент программы построения поверхности эллипсоида приведен на рис. 15.
 |

Рис. 15.




