Построение графика функции двух переменных.
Функция двух переменных имеет вид z = f (x, y) или z = z (x, y). График функции двух переменных – это некоторая поверхность в трехмерном пространстве. В MathCAD 2001 оси координат обозначаются так:
 |
Рис. 7.
Напомним, что координату x называют абсциссой, координату y – ординатой, а координату z – аппликатой. В MathCAD 2001 возможны несколько вариантов построения графика функции двух переменных.
Построение графика функции двух переменных с заданием матрицы аппликат.
Пусть задана функция двух переменных z = f (x, y) и область ее определения: x 1 £ x £ x 2, y 1 £ y £ y 2. Пусть в области определения функции f (x, y) заданы точки Mi,j = M (xi, yj), где аргументы принимают значения
xi = x 1 + (x 2 - x 1)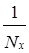 
; yj = y 1 + (y 2 - y 1) 
,
где i = 0,1, …, Nx; j = 0,1, …, Ny и Nx, Ny – целые положительные числа.
Матрица аппликат – это матрица значений функции в точках (xi, yj). Ее можно записать в виде
Mi,j = f (xi, yj), i = 0,1, …, Nx; j = 0,1, …, Ny.
Поэтому для построения графика функции с заданием матрицы аппликат следует:
1) задать границы области изменения аргументов - x 1, x 2, y 1, y 2;
2) задать индексы i, j в виде интервальных переменных, изменяющихся с шагом “1”;
3) задать область изменения аргументов x и y индексированных переменных;
4) задать матрицу аппликат Mi,j;
5) набрать и выполнить команду: Insert – Graph – Surface Plot (или щелкнуть левой клавишей мыши по кнопке 
панели инструментов Graph);
6) в структурную метку шаблона графика, расположенную около начала координат, ввести имя матрицы (без индексов).
Здесь и в дальнейшем последний заключительный пункт построения графика (команда на его построение) будет опускаться. Обозначения x 1, x 2, y 1, y 2, Mi,j, приведенные при описании процедуры построения графика, - произвольны и могут быть выбраны иными.
В качестве примера на рис. 8, 9 приведено построение графика поверхности эллиптического параболоида, каноническое уравнение которого имеет вид
,
где a, b – числовые параметры, и гиперболического параболоида, каноническое уравнение которого имеет вид
.
 |
Рис. 8.
 |
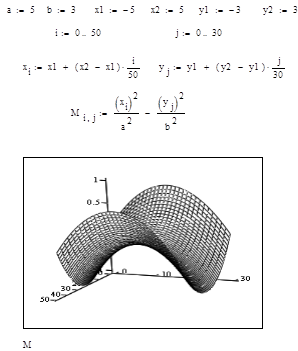Рис. 9.
