Задача 1. Случайные величины X и Y связаны соотношением mX+nY=c, где m,n,с - неслучайные величины. Найти коэффициент корреляции rxy и отношение sx/sy.
Задача 2. Случайная величина Х распределена равномерно в интервале (0, 1) и связана с Y функциональной зависимостью
Найти плотность распределения случайной величины Y.
Задача 3. Положение случайной точки с координатами (X, Y) равновероятно внутри квадрата, сторона которого равна 1, а центр совпадает с началом координат. Определить плотность вероятности с.в. Z = XY.
Задача 4. Система случайных величин (X, Y) подчинена нормальному закону распределения
Какому закону распределения подчиняется с.в. Z = X-Y?
Задача 5. Найти плотность вероятности распределения модуля радиус-вектора 
, если X и Y — нормальные случайные величины, совместная плотность вероятности которых определяется формулой
.
Задача 6. Найти плотность вероятности распределения случайной величины Z=X / Y, если
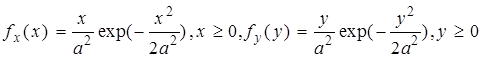
Задача 7. Совместная плотность распределения случайных величин X и Y имеет вид
.
Найти распределение с.в. Z = X / Y.
Задача 8. Задано распределение двумерной случайной величины
Найти распределение случайной величины Z = X 12+ X 22.
Задача 9. Случайные величины X и Y имеют распределения
.
Найти распределение случайных величин Z = X / Y и V = Y / X.
Задача 10. Определить плотность распределения случайной величины Z = XY, если
.
Задача 11. Оба корня квадратного уравнения 
с равной вероятностью могут принимать значения от -1 до +1. Определить плотность распределения вероятности для коэффициентов a и b.
Задача 12. Прямоугольные координаты (Х,Y) случайной точки имеют распределение
Найти плотность распределения вероятностей полярных координат
.
Задача 13. Задано нелинейное преобразование Y 1 = X 1 + X 2, Y 2 = X 1 X 2. Найти совместное распределение двумерной случайной величины (Y 1, Y 2), если (X 1, X 2) имеет двумерное нормальное распределение с параметрами m 1 = m 2 = 0, s1 =s2=s, r = 0,5.
Задача 14. Случайная величина Х распределена по закону Коши
Найти распределение величины Y = aX 2 .
Задача 15. Случайная величина Х распределена по закону Коши
Найти распределение величины Y = arc tg X .
Задача 16. Случайная точка (Х,Y) имеет постоянную плотность распределения в области 
. Найти распределение 
.
Задача 17. Найти распределение случайной величины 
, если X и Y независимы и распределены по нормальному закону с параметрами [0; 1].
Задача 18. На окружность радиуса r наудачу ставятся две точки, которые затем соединяются с центром окружности и между собой. Найти распределение и математическое ожидание площади треугольника.
