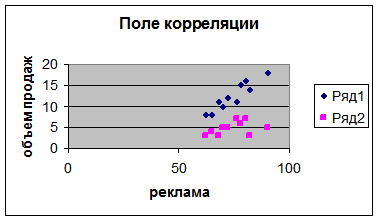
Поле корреляции: расположение пар данных на координатной плоскости представлено на рисунке 6.2.
|
 |
Уравнения и формулы в тексте курсовой работы следует выделять из текста в отдельную строку. Выше и ниже каждой формулы или уравнения должно быть оставлено не менее одной свободной строки. Если уравнение не умещается в одну строку, то оно должно быть перенесено после знака равенства (=) или после знаков плюс (+), минус (-), деления (:), умножения (´), или других математических знаков, причем знак в начале следующей строки повторяют. Пояснение значений символов и числовых коэффициентов следует приводить непосредственно под формулой в той же последовательности, в которой они даны в формуле. В курсовой работе формулы нумеруются арабскими цифрами в круглых скобках в крайнем правом положении на строке.
Пример:
|
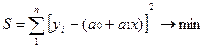
Ссылки на литературные источники по тексту работы оформляются следующим образом: после цитаты в квадратных скобках проставляется номер литературного источника по списку использованной литературы, а после запятой - номер страницы, откуда взята цитата. В случае ссылки на источники без цитирования в квадратных скобках проставляется только номер источника по списку без указания страниц. Можно оформлять ссылки в виде сноски внизу страницы. Ссылки на источники даются после каждой цитаты, использования цифрового или иного материала.
Если вы цитируете источник, обязательно нужно на него сослаться. В тексте работы все авторы, рисунки и таблицы должны иметь сноски, где будет указан источник.
Основные требования:
- сквозная нумерация на протяжении всего текста, включая приложения;
- сноски помещаются внизу той страницы, на которой было осуществлено цитирование, под текстом, и отделяются от текста короткой тонкой горизонтальной линией с левой стороны;
- знак сноски ставится непосредственно после того слова, числа, символа, предложения, к которому даётся пояснение;
- сноски оформляются шрифтом Times New Roman 10 размера с одинарным интервалом между строками;
- в конце сноски обязательно ставится номер страницы;
- когда один и тот же источник цитируется на странице несколько раз, название и выходные данные приводятся полностью только первый раз, а затем отмечается: «Там же. – С. 53»
Приведём несколько примеров оформления сносок:
_____________________
1 Максимова О.В., Махоткина А.М. Теория вероятностей и математическая статистика, г. Ростов-на-Дону, издательство Феникс 2008.
2 Г. Хан, С. Шапиро Статистические модели в инженерных задачах Москва Мир 1975г.
Список использованных источников составляют в алфавитном порядке и оформляют в соответствии с ГОСТ 7.1.-2001.
Нормативная литература (законы, подзаконные акты и т.п.) указывается в начале списка. В списке необходимо указывать фамилию и инициалы автора (авторов) источника, его название, место издания, название издательства, год опубликования и количество страниц. Название места издания (город) указывается полностью (например, Краснодар:) за исключением Москвы и Санкт-Петербурга, названия которых сокращаются (М.: и СПб.:). После места издания ставится двоеточие. Если название издательства неизвестно, то после названия места издания ставится запятая, а после нее год опубликования. В случае если у источника несколько авторов, то обязательно указываются первые три, а остальные указываются как «и др.». Если источником является коллективная монография или учебное пособие, то в начале указывается ее название, затем редактор или редакторы, место издания, издательство, год издания. При указании в качестве источника периодического издания его название располагают после названия публикации, отделяя двумя косыми чертами (//), а затем указывают через точку и тире - год, номер издания и номер страницы.
Примерный перечень заданий по курсовому проектированию к учебной дисциплине для группы 48П, 43ПК.
1. Создание математических моделей с использованием методов случайных чисел.
2. Алгоритмизация методов выявления зависимостей.
3. Использование методов выявления зависимостей в управлении производством.
4. Компьютерные модели управления ресурсами предприятия.
5. Методы оценки генеральных параметров по выборочным статистикам.
6. Модели имитации с использованием метода Монте-Карло.
7. Разработка модели оптимизации плана выпускаемой продукции.
8. Игровое моделирование и его использование в экономических задачах.
9. Разработка компьютерной модели оптимизации перевозки грузов.
10. Модель максимизации прибыли предприятия.
11. Методы выявления зависимостей в экономике.
12. Построение прогнозных моделей в экономике.
13. Модели прогнозирования по регрессии.
14. Методы оценки вероятности случайных величин.
15. Математические методы уменьшения стоимости перевозки грузов.
16. Исследование зависимостей в процессах принятия решений.
17. Методы выявления зависимостей в экономических задачах.
18. Многофакторные модели линейной регрессии.
19. Использование двойственной задачи для планирования реализации ресурсов.
20. Исследование динамики процессов в экономике.
21. Имитационные модели в экономике.
22. Модели конфликтных ситуаций.
23. Построение опорного плана перевозки грузов.
24. Модели имитации в экономических задачах.
25. Модель оптимальной реализации ограниченных ресурсов.
26. Алгоритмизация методов нахождения максимального дохода предприятия.
Примерный перечень заданий по курсовому проектированию к учебной дисциплине Группа 45 П.
1. Компьютерные модели уменьшения стоимости перевозки грузов.
2. Игровое моделирование и его использование в экономических задачах.
3. Алгоритмы оптимизации транспортных расходов.
4. Методы исследования с использованием прогнозных моделей.
5. Оптимизация стоимости реализуемых производственных ресурсов.
6. Модели в процессе оптимизации производственных планов.
7. Модель оптимального использования ограниченных ресурсов.
8. Методы нахождения максимального дохода предприятия.
9. Компьютерные модели для принятия решений в экономических задачах.
10. Построение прогнозных многофакторных моделей.
11. Модели прогнозирования в торговле и менеджменте.
12. Методы анализа дискретных случайных величин.
13. Методы построения прогнозов в экономических задачах.
14. Построение и использование многофакторных моделей регрессии.
15. Оптимизация планов производства.
16. Исследование зависимостей экономических показателей.
17. Модели конфликтных ситуаций.
18. Модели динамики в экономических задачах.
19. Экономико-математические модели для решения производственных задач.
20. Функциональные и корреляционные связи в процессах принятия решений.
21. Выборочные методы анализа экономических показателей.
22. Методы оценки надежности сложных систем.
23. Методы оптимизации производственных процессов с ограниченными ресурсами.
24. Модели прогнозирования в экономических задачах.
25. Использование двойственной задачи для планирования реализации ресурсов.
26. Модели имитации для исследования процессов в экономике.
Перечень литературы и технических средств обучения к учебной дисциплине “Математические методы”.
Основная литература.
1. А.Б.Горстко Познакомьтесь с математическим моделированим Москва Знание 1991г.
2. Бажин И.И. Информационные системы менеджмента Москва ГУ ВШЭ 2000 г.
3. Максимова О.В., Невзорова В.И. Информационные технологии для экономистов Ростов-на Дону,.Феникс 2004 г.
4. Максимова О.В. Теория вероятностей и математическая статистика Москва Дашков и Ко 2006 г.
5.: Максимова О.В., Махоткина А.М. Теория вероятностей и математическая статистика, г. Ростов-на-Дону, издательство Феникс 2008.
6. А.В Лотов Введение в экономико-математическое моделирование Москва Наука 1984г.
7. Ефимова М.П., Рябцев В.М. «Общая теория статистики» Москва Финансы и статистика 1991г.
8. Т. Нейлор «Машинные эксперименты с моделями экономических систем Москва Мир 1994г.
9. Г. Хан, С. Шапиро Статистические модели в инженерных задачах Москва Мир 1975г.
10. Г.С. Малик Основы экономики и математические методы в планировании. Москва Высшая школа 1988 г.
11. А.А. Глаголев, Т.В. Солнцева Курс высшей математики Москва Высшая школа 1971 г.
12. Айвазян С.А., Мингарян В.С Прикладная статистика и основы эконометрики. М. ЮНИТИ, 1998 г.г.
13. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. М. Финансы и статистика 1983г.
14. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Исследование зависимостей М. Финансы и статистика 1985г.
Дополнительная литература.
1. Математическое моделирование в проблемах рационального природопользования Сборник тезисов XVII школы-семинара Ростов-на-Дону – Новороссийск 1990 г.
2. Кузин С.С., Новокрещенова Л.Д., Соколова И.И. “ Применение стандартных средств Microsoft Excel в статистике ” МИПК учета и статистики, 1999 г.
3. Ефимова М.П., Рябцев В.М. “Общая теория статистики” Москва Финансы и статистика 1991г.
4. Ниворожкина Л.И. Морозова З.А. “Основы статистики с элементами теории вероятностей” Ростов -на -Дону Феникс 1999г.
5. Айвазян С.А., Мингарян В.С Практикум по прикладной статистие и эконометрике (учебное пособие). М. МЭСИ, 1998 г.г.
6. Елисеева И.И., Курышева С.В., Гордиенко Н. И др. Эконометрика. Учебное пособие Москва Финансы и статистика 2001г.
7. Елисеева И.И., Курышева С.В., Гордиенко Н. И др. Практикум по эконометрике. Учебное пособие Москва Финансы и статистика 2001г.






