Линейной комбинацией векторов a1,..., an с коэффициентами x1,..., xn называется вектор
x1a1 +... + xnan.
Чтобы разложить, вектор b по базисным векторам a1,..., an, необходимо найти коэффициенты x1,..., xn, при которых линейная комбинация векторов a1,..., an равна вектору b,
x1a1 +... + xnan = b,
при этом коэффициенты x1,..., xn, называются координатами вектора b в базисе a1,..., an.
6 Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции.
Виды матриц
1. Прямоугольные: m и n - произвольные положительные целые числа
2. Квадратные: m=n
3. Матрица строка: m=1. Например, (1 3 5 7) - во многих практических задачах такая матрица называется вектором
4. Матрица столбец: n=1. Например
5. Диагональная матрица: m=n и aij=0, если i≠j. Например
6. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,...,m
8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
9. Симметрическая матрица: m=n и aij=aji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=A
10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii)
11. Эрмитова матрица: m=n и aii=-ãii (ãji - комплексно - сопряженное к aji, т.е. если A=3+2i, то комплексно - сопряженное Ã=3-2i)
Равенство матриц
Матрицы A = || ai j || и B = || ai j || считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:

| (1) |
для любых допустимых значений индексов i и j.
К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число).
Умножение матрицы на число
При умножении матрицы A на число λ (слева или справа) каждый ее матричный элемент умножается на это число:
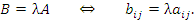
| (2) |
Сложение матриц
Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц A = || ai j || и B = || bi j || является матрица C = || ci j ||, элементы которой равны сумме соответствующих матричных элементов:
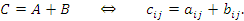
| (3) |
Линейной комбинацией матриц A и B называется выражение вида, где и – числовые коэффициенты.
7 Понятие определителя квадратной матрицы A порядка n = 1,2,3,...
Определитель – это некоторое число поставленное в соответствие квадратной матрице 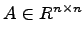 .
.
Для неквадратных матриц понятие определителя не вводится.
Для обозначения определителя квадратной матрицы A будем пользоваться обозначением 
Пусть A - произвольная квадратная матрица порядка n. Если n=1, то матрица A состоит из одного числа A. Положим по определению, что определитель такой матрицы равен числу A, т.е. 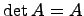 .
.
Если n=2, то матрица A имеет вид 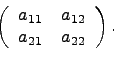
Положим по определению, что определитель такой матрицы равен 
Если n=3, то матрица A имеет вид
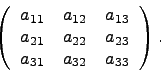
Положим по определению, что определитель такой матрицы равен 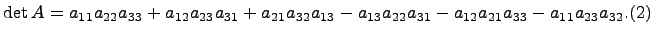
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых a i j = b j + c j (j=), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b j, в другом - из элементов c j.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число..
8 Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i =)
или j- го столбца
d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j =).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
9 Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: 
Условие существования обратной матрицы. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. det A ≠ 0.
10 Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: 
Способы нахождения обратной матрицы
Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции): 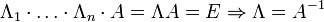
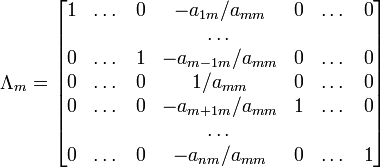
11 Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.






