Основная и расширенная матрицы системы линейных уравнений
1. Основная матрица системы линейных алгебраических уравнений
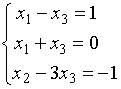имеет вид…
a. 
b.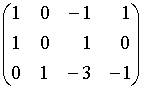 
c. 
d.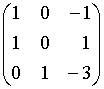 
2. Основная матрица системы линейных алгебраических уравнений
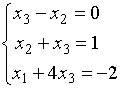имеет вид…
a.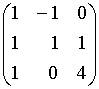 
b.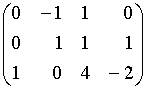 
c.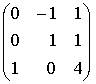 
d. 
3. Основная матрица системы линейных алгебраических уравнений
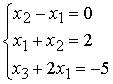имеет вид…
a. 
b.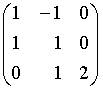 
c. 
d. 
4. Основная матрица системы линейных алгебраических уравнений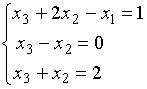 
имеет вид…
a.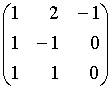 
b. 
c. 
d.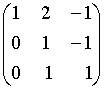 
5. Основная матрица системы линейных алгебраических уравнений
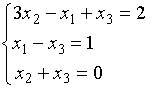имеет вид…
a.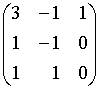 
b. 
c.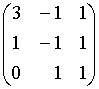 
d. 
6. Основная матрица системы линейных алгебраических уравнений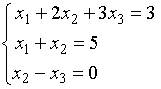 
имеет вид…
a. 
b. 
c.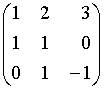 
d.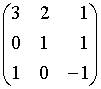 
7. Основная матрица системы линейных алгебраических уравнений 
имеет вид…
a. 
b.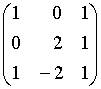 
c. 
d.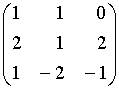 
8. Основная матрица системы линейных алгебраических уравнений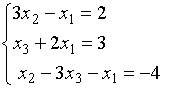 
имеет вид…
a. 
b. 
c. 
d. 
9. Основная матрица системы линейных алгебраических уравнений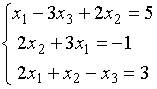 
имеет вид…
a.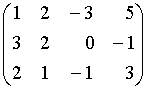 
b. 
c.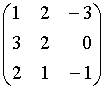 
d.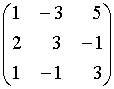 
10. Основная матрица системы линейных алгебраических уравнений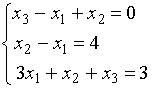 
имеет вид…
a.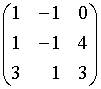 
b.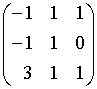 
c. 
d.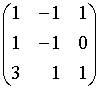 
Основные задачи аналитической геометрии на плоскости_ деление отрезка в данном отношении.
1. Даны точк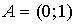и 
и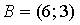 
. Тогда абсцисса середины отрезка 
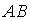равна…
a) 2
b) 3
c) – 1
d) – 3
2. Даны точк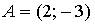и 
и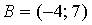 
. Тогда абсцисса середины отрезка 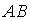равна …
a) – 1
b) 1
c) 2
d) – 5
3. Даны точки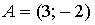 
и 
. Тогда ордината середины отрезка 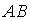равна …
a) – 3
b) 1
c) – 1
d) – 2
4. Даны точки 
и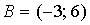 
. Тогда ордината середины отрезка 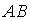равна …
a) – 1
b) 1
c) 2
d) 5
5. Даны точки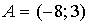 
и 
. Тогда абсцисса середины отрезка 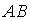равна …
a) – 1
b) – 2
c) 2
d) 1
6. Даны точк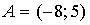и 
и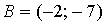 
. Тогда абсцисса середины отрезка 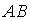равна …
a) 5
b) – 1
c) 3
d) – 5
7. Даны точк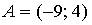и 
и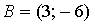 
. Тогда ордината середины отрезка 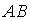равна …
a) – 3
b) – 5
c) – 1
d) 1
8. Даны точк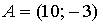и 
и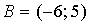 
. Тогда ордината середины отрезка 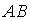равна …
a) 1
b) 4
c) – 1
d) 2
9. Даны точки 
и 
. Тогда абсцисса середины отрезка 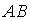равна …
a) 1
b) – 1
c) – 5
d) 2
10. Даны точки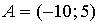 
и . Тогда абсцисса середины отрезка 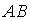равна …
a) – 9
b) – 1
c) – 2
d) 2
Основные задачи аналитической геометрии на плоскости_ площадь треугольника.
1. Площадь треугольника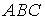 
, где 
, 
, 
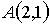, равна…
a) 14
b) 7
c) 1
d) 2
2. Площадь треугольника 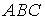, где 
, 
, 
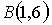, равна…
a) 6
b) 
c) 18
d) 36
3. Площадь треугольника 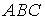, где 
, 
, 
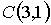, равна…
a) 3
b) 6
c)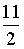 
d) 1
4. Площадь треугольника 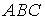, где 
, 
, 
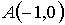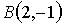, равна…
a) 5
b) 3
c) 7
d) 14
5. Площадь треугольника 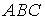, где 
, 
, 
, равна…
a) 10
b) 11
c) 22
d) 1
6. Площадь треугольника 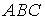, где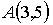 
, 
, 
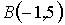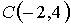, равна…
a) 4
b) 10
c) 3
d) 2
7. Площадь треугольника 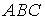, где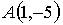 
, 
, 
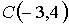, равна…
a) 31
b) 23
c)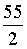 
d) 46
8. Площадь треугольника 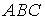, где 
, 
, 
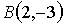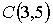, равна…
a) 2
b) 6
c) 7
d) 12
9. Площадь треугольника 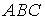, где 
, 
, 
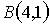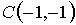, равна…
a) 6
b) 2
c) 14
d) 12
10. Площадь треугольника 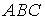, где 
, 
, 
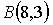, равна…
a) 8
b) 3
c) 2
d) 4
Основные задачи аналитической геометрии_ расстояние между двумя точками на плоскости.
1. Расстояние между точками 
и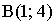 
равно…
a) 5
b) 6
c) 3
d) 4
2. Расстояние между точкам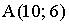и 
и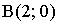 
равно…
a) 12
b) 11
c) 10
d) 9
3. Расстояние между точкам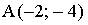и 
и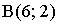 
равно…
a) 11
b) 13
c) 12
d) 10
4. Расстояние между точками 
и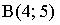 
равно…
a) 5
b) 4
c) 3
d) 6
5. Расстояние между точками 
и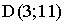 
равно…
a) 17
b) 14
c) 13
d) 12
6. Расстояние между точками и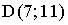 
равно…
a) 16
b) 15
c) 14
d) 21
7. Расстояние между точками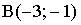 
и 
равно…
a) 14
b) 17
c) 13
d) 12
8. Расстояние между точками 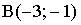и 
равно…
a) 15
b) 14
c) 21
d) 16
9. Расстояние между точкам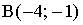и 
и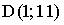 
равно…
a) 17
b) 14
c) 12
d) 13
10. Расстояние между точкам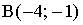и и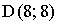 
равно…
a) 21
b) 14
c) 15
d) 16
Основные методы интегрирования_ метод интегрирования по частям.
1. Множество первообразных функции 
имеет вид…
a)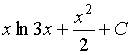 
b)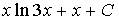 
c)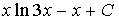 
d) 
2. Множество первообразных функции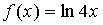 
имеет вид…
a) 
b) 
c) 
d)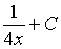 
3. Множество первообразных функции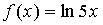 
имеет вид…
a)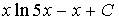 
b) 
c)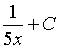 
d) 
4. Множество первообразных функции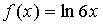 
имеет вид…
a)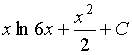 
b)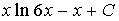 
c) 
d)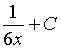 
5. Множество первообразных функции 
имеет вид…
a)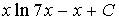 
b)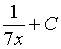 
c)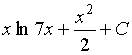 
d)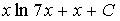 
6. Множество первообразных функции 
имеет вид…
a)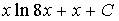 
b) 
c)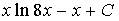 
d)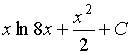 
7. Множество первообразных функции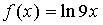 
имеет вид…
a)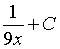 
b)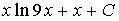 
c) 
d)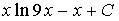 
9. Множество первообразных функции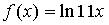 
имеет вид…
a)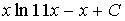 
b)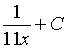 
c)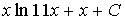 
d) 
10. Множество первообразных функции 
имеет вид…
a)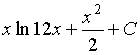 
b)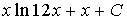 
c)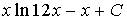 
d)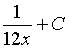 
Основные понятия теории вероятностей_ виды случайных событий.
1. Бросают 2 монеты. События А – «герб на первой монете» и В – «герб на второй монете» являются:
a) зависимыми
b) совместными
c) несовместными
d) независимыми
2. Бросают 2 монеты. События А – «цифра на первой монете» и В – «герб на второй монете» являются:
a) независимыми
b) несовместными
c) зависимыми
d) совместными
3. Бросают 2 кубика. События А – «на первом кубике выпала тройка» и В – «на втором кубике выпала шестерка» являются:
a) несовместными
b) независимыми
c) совместными
d) зависимыми
4. Бросают 2 кубика. События А – «на первом кубике выпала единица» и В – «на втором кубике выпала двойка» являются:
a) независимыми
b) зависимыми
c) совместными
d) несовместными
5. Бросают 2 кубика. События А – «на первом кубике выпала шестерка» и В – «на втором кубике выпала шестерка» являются:
a) несовместными
b) совместными
c) зависимыми
d) независимыми
6. Бросают 2 кубика. События А – «на первом кубике выпало четное» и В – «на втором кубике выпало нечетное» являются:
a) зависимыми
b) несовместными
c) совместными
d) независимыми
7. Бросают 2 кубика. События А – «выпавшее на первом кубике больше единицы» и В – «выпавшее на втором кубике меньше шести» являются:
a) независимыми
b) зависимыми
c) несовместными
d) совместными
8. Из каждой из двух колод вынимают по одной карте. События А – «карта из первой колоды - туз» и В – «карта из второй колоды - дама» являются:
a) несовместными
b) зависимыми
c) совместными
d) независимыми
9. Из каждой из двух колод вынимают по одной карте. События А – «карта из первой колоды – красной масти» и В – «карта из второй колоды – бубновой масти» являются:
a) зависимыми
b) независимыми
c) совместными
d) несовместными
10. Бросают 2 монеты. События А – «цифра на первой монете» и В – «цифра на второй монете» являются:
a) несовместными
b) независимыми
c) зависимыми
d) совместными
