АРббзШвлТРХЬлХ аХЦШЬл УРЧЮТЮУЮ ЯЮвЮЪР
І ЪгабЮТЮЩ аРСЮвХ аРббзШвлТРовбп бЫХФгойШХ аХЦШЬл ШФХРЫмЭЮУЮ ЯЮвЮЪР Т бТХаеЧТгЪЮТЮЬ бЮЯЫХ:
1) АРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг (бЮЯЫг»РТРЫп).
2) ЅХаРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т ТлеЮФЭЮЬ бХзХЭШШ a.
3) ЅХаРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т бХзХЭШШ 5.
4) ЅХаРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т бХзХЭШШ 4.
5) ґЮЧТгЪЮТЮХ вХзХЭШХ УРЧР ЯЮ ТбХЬг ЪРЭРЫг, ЭЮ ЯаШ ЪаШвШзХбЪЮЬ бЮбвЮпЭШШ УРЧЮТЮУЮ ЯЮвЮЪР Т гЧЪЮЬ бХзХЭШШ (λг= 1).
ѕСйРп ШФХп аРбзХвЮТ
БЭРзРЫР аРббзШвлТРовбп ТбХ аХЦШЬл ЯаШ pЮ=5 јїР=const, Р pa=pЭ=var.
БЫХФгойШЩ ТРаШРЭв аРбзХвЮТ ЯЮФаРЧгЬХТРХв ЯЮФ бЮСЮЩ ЯЮФСЮа вРЪЮУЮ ЧЭРзХЭШп pЮ, звЮСл pa=pЭ=101325 їР (РвЬЮбдХаЭЮХ ФРТЫХЭШХ).
ІвЮаЮЩ ТРаШРЭв аРбзХвЮТ СЮЫХХ ЯаШСЫШЦХЭ Ъ аРбзХвг аХРЫмЭЮЩ ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп, вРЪ ЪРЪ Т ФТШУРвХЫХ ЬРЪбШЬРЫмЭЮХ ФРТЫХЭШХ ЭР ТлеЮФХ ШЧ бЮЯЫР, ЪЮвЮаЮХ ЬЮЦЭЮ ФЮбвШзм, ЭХ ЬЮЦХв ЯаХТлиРвм РвЬЮбдХаЭЮХ ФРТЫХЭШХ ЭР ФРЭЭЮЩ ТлбЮвХ.
БЮФХаЦРЭШХ
АµДµА°В........................................................................................................................................................................... 2
·°ґ°Ѕёµ........................................................................................................................................................................... 3
ёБїѕ»М·ѕІ°ЅЅЛµ БёјІѕ»Л......................................................................................................................... 5
1. їЮбваЮХЭШХ ЯаЮдШЫп ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп....................................................... 6
2. АРбзсв ЯХаТЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР............................................................................. 7
3. АРбзсв ТвЮаЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР........................................................................... 16
4. АРбзсв ваХвмХУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР........................................................................ 18
5. АРбзсв зХвТсавЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР.................................................................. 21
6. АРбзсв ЯпвЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР............................................................................. 24
7. АРбзсв ШЬЯгЫмбЮТ УРЧЮТЮУЮ ЯЮвЮЪР............................................................................................ 27
8. АРбзсв бШЫ Ш впУШ........................................................................................................................................... 28
·РЪЫозХЭШХ............................................................................................................................................................. 30
БЯШбЮЪ ШбЯЮЫмЧгХЬле ШбвЮзЭШЪЮТ................................................................................................. 31
їАё»ѕ¶µЅёµ I………………………………………………………………………… 32
їАё»ѕ¶µЅёµ II………………………………………………………………………... 33
їАё»ѕ¶µЅёµ III……………………………………………………………………….. 36
ёБїѕ»М·ѕІ°ЅЅЛµ БёјІѕ»Л
r –аРФШгб, ЬЬ
S –ЯЫЮйРФм, ЬЬ2
q –УРЧЮФШЭРЬШзХбЪРп дгЭЪжШп аРбеЮФР ШЫШ ЯаШТХФХЭЭлЩ аРбеЮФ
λ –ЯаШТХФХЭЭРп бЪЮаЮбвм
M –зШбЫЮ јРеР
τ –іґД вХЬЯХаРвгал
π –іґД ФРТЫХЭШп
e –іґД ЯЫЮвЭЮбвШ
T* – вХЬЯХаРвгаР вЮаЬЮЦХЭШп, є
T – бвРвШзХбЪРп вХЬЯХаРвгаР, є
p* – ФРТЫХЭШХ вЮаЬЮЦХЭШп, їР
p – бвРвШзХбЪЮХ ФРТЫХЭШХ, їР
ρ* – ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп, ЪУ/Ь3
ρ – бвРвШзХбЪРп ЯЫЮвЭЮбвм, ЪУ/Ь3
aЪа – ЪаШвШзХбЪРп бЪЮаЮбвм ЧТгЪР, Ь/б
a – ЬХбвЭРп бЪЮаЮбвм ЧТгЪР, Ь/б
c – бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР, Ь/б
G – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР, ЪУ/б
ƒ – іґД ШЬЯгЫмбР
pЭ – ФРТЫХЭШХ ТЮ ТЭХиЭХЩ баХФХ, їР
Д – ШЬЯгЫмб УРЧЮТЮУЮ ЯЮвЮЪР, Ѕ
σЯ – ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп Т ЯапЬЮЬ бЪРзЪХ гЯЫЮвЭХЭШп
σТ.а. – ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп ЯаШ ТЭХЧРЯЭЮЬ аРбиШаХЭШШ
σВ – ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп ЯаШ ЯЮФТЮФХ вХЯЫЮвл
P0-г – бШЫР ТЮЧФХЩбвТШп УРЧЮТЮУЮ ЯЮвЮЪР ЭР ФЮЧТгЪЮТго зРбвм бЮЯЫР, Ѕ
Pг-a – бШЫР ТЮЧФХЩбвТШп УРЧЮТЮУЮ ЯЮвЮЪР ЭР бТХаеЧТгЪЮТго зРбвм бЮЯЫР, Ѕ
P0-a – бШЫР ТЮЧФХЩбвТШп УРЧЮТЮУЮ ЯЮвЮЪР ЭР бЮЯЫЮ Т жХЫЮЬ, Ѕ
PТЭгв. – ТЭгваХЭЭпп бЮбвРТЫпойРп ЯЮЫЭЮЩ впУШ, Ѕ
PЭРа. – ЭРагЦЭРп бЮбвРТЫпойРп ЯЮЫЭЮЩ впУШ, Ѕ
P – ЯЮЫЭРп впУР ФТШУРвХЫп, Ѕ
їЮбваЮХЭШХ ЯаЮдШЫп ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп.
АРббзШвРХЬ ЯРаРЬХвал аРЪХвЭЮУЮ ФТШУРвХЫп б ЯЮЬЮймо ШбеЮФЭле ФРЭЭле:
1) ФЫШЭР ЪРЬХал бУЮаРЭШп:
 ,
,
2) ФЫШЭР ФЮЧТгЪЮТЮЩ зРбвШ бЮЯЫР:
 ,
,
3) ФЫШЭР бТХаеЧТгЪЮТЮЩ зРбвШ бЮЯЫР:
 ,
,
4) аРФШгб ЪРЬХал бУЮаРЭШп:
 ;
;
5) аРФШгб УРЧЮТЮУЮ ЯЮвЮЪР ЯаШ ТеЮФХ Т ЪРЬХаг бУЮаРЭШп:
 ,
,
6) аРФШгб ТлеЮФЭЮУЮ бХзХЭШп бЮЯЫР:

їЮ аРббзШвРЭЭлЬ ЯРаРЬХваРЬ ЯЮбваЮШЬ ЯаЮдШЫм ЪРЬХал бУЮаРЭШп (бЬ. ЯаШЫЮЦХЭШХ бва. 23) їЮ ЯаЮдШЫо ЪРЬХал ЮЯаХФХЫпХЬ аРФШгбл ЯаЮЬХЦгвЮзЭле аРбзсвЭле бХзХЭШЩ r2, r3, r4, r5.
АРббзШвлТРХЬ ЯЫЮйРФШ ТбХе бХзХЭШЩ ЯЮ дЮаЬгЫХ S=πr2, УФХ r – аРФШгб, ЬЬ.
їЮЫгзХЭЭлХ ФРЭЭлХ ЯаШТХФХЭл Т вРСЫШжХ 1:
ВРСЫШжР 1
| р бХзХЭШп | Ъ | г | Р | ||||||
| r, ЬЬ | 27.512 | 43.5 | 43.5 | 35.48 | 29.99 | 36.23 | 47.87 | 55.97 | |
S, 
| 2377.90 | 5944.68 | 5944.68 | 3954.73 | 2825.55 | 2642.08 | 4123.69 | 7199.08 | 9841.48 |
| x, ЬЬ | 20.30 | 55.638 | 71.621 | 82.276 | 101.3 | 139.348 | 177.396 |
2. АРбзсв ЯХаТЮУЮ аРбзХвЭЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР (аХЧгЫмвРвл ШббЫХФЮТРЭШп pЮ= var, pЭ=101325 јїР)
АРббзШвРХЬ ЯРаРЬХвал ЯЮвЮЪР ЯаШ бТХаеЧТгЪЮТЮЬ ШбвХзХЭШШ УРЧР ШЧ бЮЯЫР.
1) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «Ъ»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
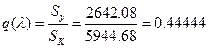 ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 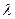 k ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
k ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 ,
,  ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:


їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:

2) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «0»:
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 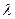 0 ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЪЮЫШзХбвТР ФТШЦХЭШп ФЫп УРЧР, ЭРеЮФпйХУЮбп Т ЪРЬХаХ бУЮаРЭШп ЬХЦФг бХзХЭШпЬШ «0» Ш «k», гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
0 ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЪЮЫШзХбвТР ФТШЦХЭШп ФЫп УРЧР, ЭРеЮФпйХУЮбп Т ЪРЬХаХ бУЮаРЭШп ЬХЦФг бХзХЭШпЬШ «0» Ш «k», гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 ,
,
ґЫп ЭРеЮЦФХЭШп  ЯаШЬХЬ
ЯаШЬХЬ 
АХиХЭШХ 
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:



їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:




3) ІлзШбЫШЬ ЮбвРТиШХбп ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР Т бХзХЭШШ «k»:
ЅРЩФХЬ ЧЭРзХЭШХ ФРТЫХЭШп ШЧ ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЭХаРЧалТЭЮбвШ ФЫп ЦШТле бХзХЭШЩ «0» Ш «k» УРЧЮТЮУЮ ЯЮвЮЪР:  ;
;

ѕбвРЫмЭлХ ЯРаРЬХвал ТлзШбЫШЬ бЫХФгойШЬ ЮСаРЧЮЬ:


4) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «1»:
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 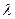 1 ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЪЮЫШзХбвТР ФТШЦХЭШп ФЫп УРЧР, ЭРеЮФпйХУЮбп Т ЪРЬХаХ бУЮаРЭШп ЬХЦФг бХзХЭШпЬШ «1» Ш «є», гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
1 ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЪЮЫШзХбвТР ФТШЦХЭШп ФЫп УРЧР, ЭРеЮФпйХУЮбп Т ЪРЬХаХ бУЮаРЭШп ЬХЦФг бХзХЭШпЬШ «1» Ш «є», гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 , УФХ
, УФХ  ;
;
ґЫп ЭРеЮЦФХЭШп  ЯаШЬХЬ
ЯаШЬХЬ 
АХиХЭШХ 
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:



їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:

ЅРЩФХЬ ЧЭРзХЭШХ p1 ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЭХаРЧалТЭЮбвШ:
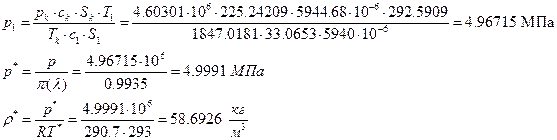



5) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «2»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
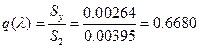 ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 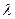 ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 ,
,  ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:


їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:

їЮбЫХ бХзХЭШп «k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:



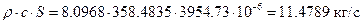
6) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «3»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
 ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 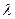 ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 ,
,  ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:


їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
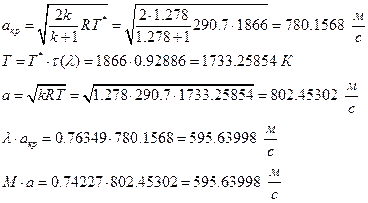
їЮбЫХ бХзХЭШп «k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
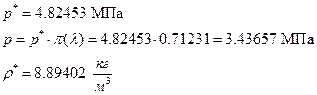

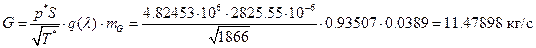

7) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «г»:
ґРЭЭЮХ бХзХЭШХ ЪаШвШзХбЪЮХ, ЯЮнвЮЬг: q(λ)=1, λ =1, M=1.
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:

їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
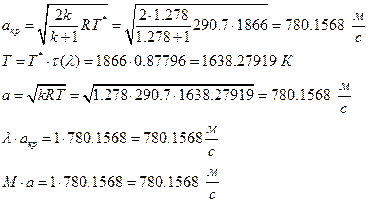
їЮбЫХ бХзХЭШп «k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:




8) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «4»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
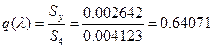 ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 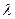 ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 ,
,  ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
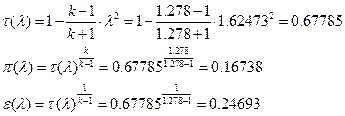
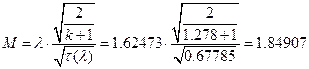
їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:

їЮбЫХ бХзХЭШп «k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:



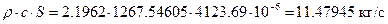
9) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «5»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
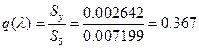 ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 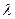 ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 ,
,  ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
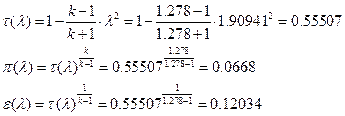
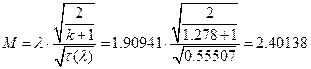
їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:


їЮбЫХ бХзХЭШп «k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:




10) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «a»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
 ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг 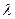 ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп, гзШвлТРп звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.  :
:
 ,
,  ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:


їРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
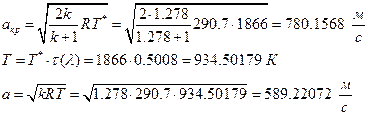

їЮбЫХ бХзХЭШп «k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:










