Вопросы, подлежащие изучению
1. Понятие символьных вычислений.
2. Создание и работа с символьными переменными, выражениями и функциями.
3. Аналитическое вычисление конечных и бесконечных сумм и произведений.
4. Операция подстановки значения переменной в выражение.
5. Вычисление пределов и производных.
6. Аналитическое и численное дифференцирование функции в точке.
7. Символьное и численное вычисление интегралов.
Задание
1. Выбрать вариант задания из табл. 3.3-1.
Создать М-файл
Выполнить символьные операции с выражениями
Упростить любое выражение.
Разложить f3 на слагаемые и полученное выражение упростить.
Выполнить операцию подстановки значения переменной (k) в выражение f2 (k - выражение на которое заменяется переменная х).
Получить обратную функцию к f3.
Разложить f3 на простые множители.
Выполнить операцию комплектования f3 по степеням.
Рассчитать численное значение выражения f2 с 5-ю знаками точности (значения переменных, входящих в состав данного выражения, выбрать самостоятельно).
Выполнить символьные операции математического анализа
Разложить f2 в ряд Тейлора.
Вычислить различные пределы от f4.
Вычислить первые и вторые производные от f3 и f4 в символьном виде и в выбранной точке.
Вычислить неопределенные и определенные интегралы от f4.
2.5. Решить уравнение f3=0.
Отладить, выполнить и создать документ М-файла
Примечание: Если переменной х присвоено значение, то оно распространяется на все ниже следующие вычисления, проводимые в данном документе. Поэтому при проведении символьных вычислений рекомендуется изменить имя переменной или обнулять......
Варианты задания
Таблица 3.3-1

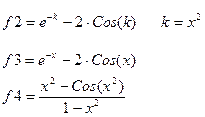
| 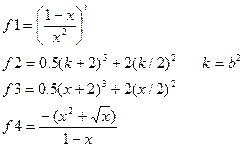
| ||

| 
| ||

| 
| ||
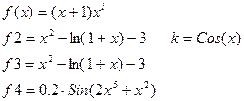
| 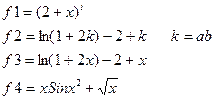
| ||

| 
| ||

| 
| ||
| 
| ||

| 
| ||

| 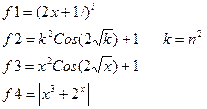
| ||

| 
| ||

| 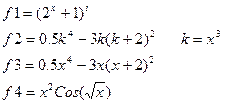
| ||
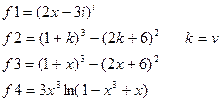
| 
| ||

| 
| ||

| 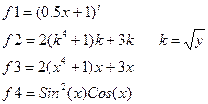
| ||

| 
|
Содержание отчета
1. Название лабораторной работы.
2. Индивидуальное задание.
3. Документ с исходным текстом (М-файлом)
4. Протокол вычислений
Пример выполнения задания
1. Выбрать вариант задания:
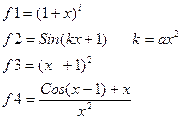
Создать М-файл
| 3. clear all 4. echo on 5. %1. Выполнить символьные операции с выражениями 6. % 7. % 1.1. Упростить выражение. 8. syms a b; 9. simplify((a+b-a)/(2*a)) 10. % 11. % 12. % 1.2.Разложения f3 на слагаемые и 13. % обратное преобразование по упрощению полученного выражения. 14. syms x; 15. f3=(x+1).^2 16. expand(f3) 17. simplify(ans) 18. % 19. % 20. % 1.3.Подстановка значения переменной k в выражение f2. 21. syms k a x 22. f2=sin(k*x + 1) 23. subs(f2,k,a*x.^2) 24. % 25. % 26. % 1.4.Обращение F3 27. finverse(f3) 28. % 29. % 30. % 1.5.Разложение на простые множители f3 31. factor(f3) 32. % 33. % 34. 35. % 1.6. Комплектование по степеням f3 36. sym x='x': f3=(x+1)^2 37. collect(f3) 38. % 39. % 40. % 1.7.Результаты получения численного значения выражения f2 с 5-мя знаками. 41. x=0.55: k=3 42. vpa(f2,5) 43. vpa(sin(a*x^3+1),4) 44. % 45. % 46. % 2. Выполнить Символьные операции математического анализа 47. % 48. %2.1. Разложение функций в ряд Тейлора – taylor() 49. syms a x 50. x=2 51. f22=sin(a*x^3+1) 52. taylor(f22) 53. pretty(ans) 54. % 55. % 56. %2.2. Вычисление пределов 57. z=sym('z') 58. limit((cos(z-1)+z)/z.^2) 59. limit((cos(z-1))/z.^2) 60. limit((cos(z-1)+z)/z.^2,pi/2) 61. % 62. % 63. %2.3. Вычисление производных 64. sym z: sym x='x' 65. f3=sym('(z+1)^2') 66. diff(f3) 67. diff(f3,2) 68. f4=(cos(x-1)+x)./x.^2 69. diff(f4) 70. diff(f4,2) 71. % 72. % 73. %2.4. Вычисление неопределенных и определенных интегралов 74. z=sym('z') 75. int((cos(z-1)+z)/z.^2,z) 76. int((cos(z-1)+z)/z.^2,z,1,4) 77. int((cos(z-1)+z)/z.^2,z,1,2) 78. % 79. % 80. %2.5. Решение алгебраических уравнений 81. sym z 82. f3=sym('(z+1)^2') 83. solve(f3) 84. echo off |
Сохранть под именем xxx.m
Выполнть М-файл xxx.m
Создать документ с результатами вычисления
| clear allecho on%1. Выполнить символьные операции с выражениями%% 1.1. Упростить выражение.syms a b;simplify((a+b-a)/(2*a))%%% 1.2.Разложения f3 на слагаемые и% обратное преобразование по упрощению полученного выражения.syms x;f3=(x+1).^2expand(f3)simplify(ans)%%% 1.3.Подстановка значения переменной k в выражение f2.syms k a xf2=sin(k*x + 1)subs(f2,k,a*x.^2)%%% 1.4.Обращение F3finverse(f3)%%% 1.5.Разложение на простые множители f3factor(f3)%%% 1.6. Комплектование по степеням f3sym x='x'f3=(x+1)^2collect(f3)%%% 1.7.Результаты получения численного значения выражения f2 с 5-мя знаками.x=0.55k=3vpa(f2,5)vpa(sin(a*x^3+1),4)%%% 2. Выполнить Символьные операции математического анализа%%2.1. Разложение функций в ряд Тейлора – taylor()syms a x: x=2f22=sin(a*x^3+1)taylor(f22)pretty(ans)%%%2.2. Вычисление пределовz=sym('z')limit((cos(z-1)+z)/z.^2)limit((cos(z-1))/z.^2)limit((cos(z-1)+z)/z.^2,pi/2)%%%2.3. Вычисление производныхsym zsym x='x'f3=sym('(z+1)^2')diff(f3)diff(f3,2)f4=(cos(x-1)+x)./x.^2diff(f4)diff(f4,2)%%%2.4. Вычисление неопределенных и определенных интеграловz=sym('z')int((cos(z-1)+z)/z.^2,z)int((cos(z-1)+z)/z.^2,z,1,4)int((cos(z-1)+z)/z.^2,z,1,2)%%%2.5. Решение алгебраических уравненийsym zf3=sym('(z+1)^2')solve(f3)echo off%%1. Выполнить символьные операции с выражениями%% 1.1. Упростить выражение.syms a b;simplify((a+b-a)/(2*a))ans =b/(2*a)%%% 1.2.Разложения f3 на слагаемые и % обратное преобразование по упрощению полученного выражения.syms x;f3=(x+1).^2f3 =(x + 1)^2expand(f3)ans =x^2 + 2*x + 1simplify(ans)ans =(x + 1)^2%%% 1.3.Подстановка значения переменной k в выражение f2.syms k a xf2=sin(k*x + 1)f2 =sin(k*x + 1)subs(f2,k,a*x.^2)ans =sin(a*x^3 + 1)%%% 1.4.Обращение F3finverse(f3)Warning: Functional inverse is not unique. ans =x^(1/2) - 1%%% 1.5.Разложение на простые множители f3factor(f3)ans =(x + 1)^2%%% 1.6. Комплектование по степеням f3sym x='x'ans =x = xf3=(x+1)^2f3 =(x + 1)^2collect(f3)ans =x^2 + 2*x + 1%%% 1.7.Результаты получения численного значения выражения f2 с 5-мя знаками.x=0.55x = 0.5500k=3k = 3vpa(f2,5)ans =sin(k*x + 1.0)vpa(sin(a*x^3+1),4) ans =sin(0.1664*a + 1.0)%%% 2. Выполнить Символьные операции математического анализа%%2.1. Разложение функций в ряд Тейлора – taylor()syms a xx=2x = 2f22=sin(a*x^3+1)f22 =sin(8*a + 1)taylor(f22)ans =(4096*cos(1)*a^5)/15 + (512*sin(1)*a^4)/3 - (256*cos(1)*a^3)/3 - 32*sin(1)*a^2 + 8*cos(1)*a + sin(1) pretty(ans) 5 4 3 4096 cos(1) a 512 sin(1) a 256 cos(1) a -------------- + ------------- - ------------- - 15 3 3 2 32 sin(1) a + 8 cos(1) a + sin(1)%%%2.2. Вычисление пределовz=sym('z')z =zlimit((cos(z-1)+z)/z.^2)ans =Inflimit((cos(z-1))/z.^2)ans =Inflimit((cos(z-1)+z)/z.^2,pi/2)ans =(4*(pi/2 + cos(pi/2 - 1)))/pi^2%%%2.3. Вычисление производныхsym z ans =zsym x='x'ans =x = xf3=sym('(z+1)^2')f3 =(z + 1)^2diff(f3)ans =2*z + 2diff(f3,2)ans =2f4=(cos(x-1)+x)./x.^2f4 = 0.6351diff(f4)ans = []diff(f4,2)ans = []%%%2.4. Вычисление неопределенных и определенных интегралов z=sym('z')z =zint((cos(z-1)+z)/z.^2,z)ans =log(z) - cos(z - 1)/z + sin(1)*cosint(z) - cos(1)*sinint(z)int((cos(z-1)+z)/z.^2,z,1,4)ans =log(4) - cos(3)/4 - cosint(1)*sin(1) + cosint(4)*sin(1) + sinint(1)*cos(1) - sinint(4)*cos(1) + 1int((cos(z-1)+z)/z.^2,z,1,2)ans =log(2) - cos(1)/2 - cosint(1)*sin(1) + cosint(2)*sin(1) + sinint(1)*cos(1) - sinint(2)*cos(1) + 1%%%2.5. Решение алгебраических уравнений sym zans =zf3=sym('(z+1)^2')f3 =(z + 1)^2solve(f3)ans = -1 -1echo off clear all |
clear allecho on%1. Выполнить символьные операции с выражениями%% 1.1. Упростить выражение.syms a b;simplify((a+b-a)/(2*a))%%% 1.2.Разложения f3 на слагаемые и% обратное преобразование по упрощению полученного выражения.syms x;f3=(x+1).^2expand(f3)simplify(ans)%%% 1.3.Подстановка значения переменной k в выражение f2.syms k a xf2=sin(k*x + 1)subs(f2,k,a*x.^2)%%% 1.4.Обращение F3finverse(f3)%%% 1.5.Разложение на простые множители f3factor(f3)%% % 1.6. Комплектование по степеням f3sym x='x'f3=(x+1)^2collect(f3)%%% 1.7.Результаты получения численного значения выражения f2 с 5-мя знаками.x=0.55k=3vpa(f2,5)vpa(sin(a*x^3+1),4)%%% 2. Выполнить Символьные операции математического анализа%%2.1. Разложение функций в ряд Тейлора – taylor()syms a xx=2f22=sin(a*x^3+1)taylor(f22)pretty(ans)%%%2.2. Вычисление пределовz=sym('z')limit((cos(z-1)+z)/z.^2)limit((cos(z-1))/z.^2)limit((cos(z-1)+z)/z.^2,pi/2)%%%2.3. Вычисление символьного значения производных и% их значение в точках z=2 и x=2sym zsym x='x'f3=sym('(z+1)^2')ff3=diff(f3)z=2subs(ff3)diff(f3,2)f4=sym('(cos(x-1)+x)/x^2')ff4=diff(f4)x=2subs(ff4)diff(f4,2)%%%2.4. Вычисление неопределенных и определенных интеграловz=sym('z')int((cos(z-1)+z)/z.^2,z)int((cos(z-1)+z)/z.^2,z,1,4)int((cos(z-1)+z)/z.^2,z,1,2)%%%2.5. Решение алгебраических уравненийsym zf3=sym('(z+1)^2')solve(f3)echo off






