Гиниатуллина Р.А.
Проверил: Родионов В.В.
Казань, 2012
Содержание:
1. Определение ЗЛП_____________________________________3
2. Первый алгоритм симплекс – метода___________________4-7
3. Алгоритм обратной матрицы_________________________7-11
4. О конечности симплекс – метода_____________________11-12
5. Алгоритм построения начального опорного плана______12-14
6. Алгоритм искусственного базиса____________________14-15
7. Список литературы__________________________________16
Определение ЗЛП.
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
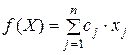 (9.1)
(9.1)
при условиях


| (9.2) |

| (9.3) |

| (9.4) |
где  - заданные постоянные величины и
- заданные постоянные величины и  .
.
Функция (9.1) называется целевой функцией (или линейной формой) задачи (9.1)-(9.4), а условия (9.2)-(9.4) – ограничениями данной задачи.
Канонической или о сновной задачей линейного программирования называется задача, которая состоит в определении максимального значения функции
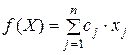 (9.5)
(9.5)
при выполнении условий:

| (9.6) |

| (9.7) |
где  .
.
Первый алгоритм симплекс метода
Приведём описание алгоритма применительно к ЗЛП, записанной в канонической форме с односторонними ограничениями:

Пусть известен начальный опорный план  с базисом
с базисом 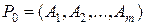 , т.е.
, т.е.  - базисные компоненты,
- базисные компоненты,  - небазисные компоненты.
- небазисные компоненты.
Вычисления удобно выполнять, заполняя следующую симплекс-таблицу:
| C | 
| … | 
| … | 
| ||||
| № | 
| P | B | 
| … | 
| … | 
| t |

| 
| 
| 
| … | 
| … | 
| ||
| … | … | … | … | … | … | … | … | … | |

| 
| 
| 
| 
| … | … | 
| 
| |
| … | … | … | … | … | … | … | … | … | |
| m | 
| 
| 
| 
| … | 
| … | 
| |

| 
| 
| … | 
| … | 
|
Порядок вычислений по первому алгоритму:
Шаг 1. Найти обратную к  матрицу
матрицу  .
.
Шаг 2. Вычислить коэффициенты разложения векторов условий 
 по базису
по базису  , используя расчётную формулу:
, используя расчётную формулу:

и заполнить ими столбцы  симплекс-таблицы нулевой итерации.
симплекс-таблицы нулевой итерации.
Шаг 3. Вычислить значение линейной формы  , как скалярное произведение
, как скалярное произведение  соответствующих столбцов симплекс-таблицы, и значения оценок
соответствующих столбцов симплекс-таблицы, и значения оценок  векторов условий
векторов условий  относительно базиса
относительно базиса  в соответствии с формулой
в соответствии с формулой 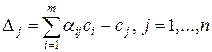 как скалярное произведение столбцов
как скалярное произведение столбцов  и
и  симплекс-таблицы без коэффициента
симплекс-таблицы без коэффициента  , т.е. по расчётной формуле
, т.е. по расчётной формуле 
Полученными значениями заполнить  -ю строку симплекс-таблицы.
-ю строку симплекс-таблицы.
Шаг 4. Проверить оптимальность опорного плана.
· Если  , то
, то  - оптимальный опорный план и, тогда, в столбце
- оптимальный опорный план и, тогда, в столбце  симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
· Если хотя бы в одном столбце с отрицательной оценкой  все элементы меньше или равны 0
все элементы меньше или равны 0  , то линейная форма
, то линейная форма  не ограничена сверху и решения ЗЛП не существует. На этом процесс решения ЗЛП также завершается.
не ограничена сверху и решения ЗЛП не существует. На этом процесс решения ЗЛП также завершается.
· Если же в каждом столбце с отрицательными оценками найдется хотя бы один положительный элемент  , то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки
, то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки  и, таким образом, определяется разрешающий столбец
и, таким образом, определяется разрешающий столбец  .
.
Шаг 5. Определить вектор, исключаемый из базиса для чего необходимо заполнить последний столбец t симплекс-таблицы нулевой итерации путем деления элементов столбца  на соответствующие им по номеру положительные элементы разрешающего столбца
на соответствующие им по номеру положительные элементы разрешающего столбца  , т.е.
, т.е.  ,
,
При этом, в строках столбца  , соответствующих неположительным элементам
, соответствующих неположительным элементам  , записываем
, записываем  , не выполняя деления.
, не выполняя деления.
Далее необходимо выбрать  . Если
. Если  достигается на нескольких позициях столбца
достигается на нескольких позициях столбца  , то из базиса может быть исключен любой из векторов
, то из базиса может быть исключен любой из векторов  . Для определенности, договоримся исключать из них вектор с наименьшим номером.
. Для определенности, договоримся исключать из них вектор с наименьшим номером.
Пусть  получился на
получился на  -той позиции, т.е.
-той позиции, т.е.  , тогда соответствующий этому индексу вектор
, тогда соответствующий этому индексу вектор  должен выводиться из базиса. Строка симплекс-таблицы, соответствующая этому индексу, называется разрешающей строкой. Элемент
должен выводиться из базиса. Строка симплекс-таблицы, соответствующая этому индексу, называется разрешающей строкой. Элемент  , стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
, стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
Шаг 6. Заполнить новую симплекс-таблицу в следующей последовательности.
· На  -тых позициях столбцов
-тых позициях столбцов  и
и  записать соответственно
записать соответственно  и
и  , а на остальных позициях этих столбцов оставить прежние элементы.
, а на остальных позициях этих столбцов оставить прежние элементы.
· Заполнить  -тую строку новой симплекс-таблицы элементами
-тую строку новой симплекс-таблицы элементами  , получающимися делением соответствующих элементов (
, получающимися делением соответствующих элементов ( )
)  -той строки старой симплекс-таблицы на разрешающий элемент
-той строки старой симплекс-таблицы на разрешающий элемент  , т.е. по формулам
, т.е. по формулам 
· Все остальные  -тые строки главной части новой симплекс-таблицы получить как результат вычитания из
-тые строки главной части новой симплекс-таблицы получить как результат вычитания из  -той строки старой симплекс-таблицы
-той строки старой симплекс-таблицы  -той строки новой симплекс-таблицы, умноженной на соответствующий
-той строки новой симплекс-таблицы, умноженной на соответствующий  -тый элемент разрешающего столбца, т.е. в соответствии с рекуррентными формулами
-тый элемент разрешающего столбца, т.е. в соответствии с рекуррентными формулами 

 ,
,  . По аналогичным формулам вычисляются также и элементы
. По аналогичным формулам вычисляются также и элементы  -й строки новой таблицы:
-й строки новой таблицы:  ,
,  ,
,  .
.
Этим завершается построение новой симплекс-таблицы.
Описанный процесс построения симплекс-таблиц повторяется до получения оптимального опорного плана или до установления неограниченности линейной формы, т.е. неразрешимости ЗЛП.
Если среди оценок  небазисных векторов условий
небазисных векторов условий  относительно базиса найденного оптимального опорного плана найдется хотя бы одна равная нулю, то это означает, что ЗЛП имеет неединственное решение.
относительно базиса найденного оптимального опорного плана найдется хотя бы одна равная нулю, то это означает, что ЗЛП имеет неединственное решение.
Алгоритм обратной матрицы
Опишем алгоритм применительно к решению ЗЛП, записанной в канонической форме с односторонними ограничениями:

 Пусть известен начальный опорный план
Пусть известен начальный опорный план  с базисом
с базисом 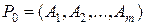 , т.е.
, т.е.  - базисные компоненты,
- базисные компоненты,  - небазисные компоненты.
- небазисные компоненты.
В данном методе все параметры итерации, необходимые для оценки плана на оптимальность и перехода к лучшему плану, вычисляются через элементы  обратной матрицы
обратной матрицы  . Поэтому второй алгоритм симплекс-метода также называют алгоритмом обратной матрицы.
. Поэтому второй алгоритм симплекс-метода также называют алгоритмом обратной матрицы.
Вычисления удобно выполнять, используя две симплекс-таблицы:
Основная таблица
| № | 
| P | 
| 
| … | 
| 
| t |

| 
| 
| 
| … | 
| 
| … | |
| … | … | … | … | … | … | … | … | … |

| 
| 
| 
| 
| … | 
| 
| 
|
| … | … | … | … | … | … | … | … | … |

| 
| 
| 
| 
| … | 
| 
| … |

| 
| 
| … | 
| 
|
Вспомогательная таблица
| № | 
| 
| … | 
|

| 
| … | 
| |
| … | … | … | … | … |

| 
| 
| … | 
|

| 
| … | 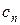
| |

| 
| … | 
| |

| 
| … | 
| |

| 
| … | 
| |
| … | … | … | … | … |
Порядок вычислений по второму алгоритму
Шаг 1. Найти обратную матрицу  и заполнить её элементами
и заполнить её элементами  столбцы
столбцы  , основной симплекс-таблицы.
, основной симплекс-таблицы.
Шаг 2. Вычислить значение линейной формы  как скалярное произведение столбцов
как скалярное произведение столбцов  и
и  основной таблицы. Результат занести в
основной таблицы. Результат занести в  строку столбца
строку столбца  основной симплекс-таблицы.
основной симплекс-таблицы.
Шаг 3. Вычислить значения  элементов вектора-строки
элементов вектора-строки  по формуле
по формуле  , как скалярное произведение столбцов
, как скалярное произведение столбцов  и
и  основной симплекс-таблицы. Полученными значениями заполнить
основной симплекс-таблицы. Полученными значениями заполнить  -ю строку основной симплекс-таблицы.
-ю строку основной симплекс-таблицы.
Шаг 4. Найти значения оценок  векторов условий
векторов условий  относительно базиса по формуле
относительно базиса по формуле  ,
,  , как произведение вектора-строки
, как произведение вектора-строки  основной таблицы на соответствующий столбец
основной таблицы на соответствующий столбец  вспомогательной таблицы минус соответствующий коэффициент
вспомогательной таблицы минус соответствующий коэффициент  линейной формы, записанный в
линейной формы, записанный в  -ой строке вспомогательной таблицы. Полученные значения занести в строку вспомогательной таблицы с номером, соответствующим номеру выполняемой итерации.
-ой строке вспомогательной таблицы. Полученные значения занести в строку вспомогательной таблицы с номером, соответствующим номеру выполняемой итерации.
Шаг 5. Проверить оптимальность опорного плана.
· Если все оценки неотрицательные ( ), то
), то  - оптимальный опорный план и, тогда, в столбце
- оптимальный опорный план и, тогда, в столбце  основной симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
основной симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
· Если среди оценок найдутся отрицательные ( ), то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки
), то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки 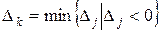 и, таким образом, устанавливается разрешающий столбец
и, таким образом, устанавливается разрешающий столбец  .
.
Шаг 6. Вычислить коэффициенты разложения  вектора
вектора  по базису
по базису  , используя формулу
, используя формулу  , как произведение
, как произведение  -ой строки обратной матрицы
-ой строки обратной матрицы  из основной таблицы на столбец
из основной таблицы на столбец  вспомогательной таблицы. Полученные значения занести в столбец
вспомогательной таблицы. Полученные значения занести в столбец  основной симплекс-таблицы.
основной симплекс-таблицы.
Шаг 7. Определить вектор, выводимый из базиса. Для этого необходимо заполнить столбец  основной таблицы значениями
основной таблицы значениями  путем деления элементов столбца
путем деления элементов столбца  основной таблицы на соответствующие им по номеру элементы столбца
основной таблицы на соответствующие им по номеру элементы столбца  основной таблицы.
основной таблицы.
· Если все 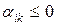
 , то исходная задача неразрешима в силу неограниченности сверху линейной формы
, то исходная задача неразрешима в силу неограниченности сверху линейной формы 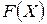 . На этом процесс решения ЗЛП завершается.
. На этом процесс решения ЗЛП завершается.
· Если 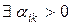 , то необходимо выбрать
, то необходимо выбрать  . Пусть им оказался элемент с номером
. Пусть им оказался элемент с номером  , т.е.
, т.е.  . Тогда соответствующий этому индексу
. Тогда соответствующий этому индексу  вектор
вектор  должен выводиться из базиса. Элемент
должен выводиться из базиса. Элемент  является «разрешающим». На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
является «разрешающим». На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
Шаг 8.Для заполнения новой основной таблицы вычислить по рекуррентным формулам новые значения параметров итерации.
· Заполнить  -тую строку новой основной таблицы элементами
-тую строку новой основной таблицы элементами  ,
,  , получающимися делением соответствующих элементов (
, получающимися делением соответствующих элементов ( )
)  -той строки старой основной таблицы на разрешающий элемент
-той строки старой основной таблицы на разрешающий элемент  , т.е. по формулам
, т.е. по формулам  .
.
· Все остальные  -тые строки главной части новой основной симплекс-таблицы получить как результат вычитания из
-тые строки главной части новой основной симплекс-таблицы получить как результат вычитания из  -той строки старой основной симплекс-таблицы
-той строки старой основной симплекс-таблицы  -той строки новой симплекс-таблицы, умноженной на соответствующий
-той строки новой симплекс-таблицы, умноженной на соответствующий  -тый элемент разрешающего столбца
-тый элемент разрешающего столбца  старой основной симплекс-таблицы, т.е. в соответствии с рекуррентными формулами
старой основной симплекс-таблицы, т.е. в соответствии с рекуррентными формулами 
 . По аналогичным формулам могут быть вычислены также и элементы
. По аналогичным формулам могут быть вычислены также и элементы  -й строки:
-й строки: 
 .
.
Описанный процесс построения симплекс-таблиц повторяется до получения оптимального опорного плана или до установления неограниченности линейной формы, т.е. неразрешимости ЗЛП.
4. О конечности симплекс – метода
Пусть ЗЛП является невырожденной. Тогда на каждом шаге симплекс – метода будем иметь  . Процесс расчета будет состоять в переходе
. Процесс расчета будет состоять в переходе
 ,
,
где два соседних базиса отличаются лишь одним вектором. Например, переход от  к
к  осуществлен введением вектора
осуществлен введением вектора  . При этом линейная форма изменится так:
. При этом линейная форма изменится так:
 ,
,
т.к.  и
и  .
.
Таким образом, при переходе от одного опорного плана к другому в невырожденной задаче линейная форма возрастает. Поэтому невозможен возврат к старому опорному плану, т.е. каждый шаг симплекс – метода приводит к новому, ранее не встречавшемуся, опорному плану. И поскольку число опорных планов (вершин многогранного множества  ) конечно, то в невырожденной задаче через конечное число шагов либо устанавливается неограниченность линейной формы, либо получается оптимальный план.
) конечно, то в невырожденной задаче через конечное число шагов либо устанавливается неограниченность линейной формы, либо получается оптимальный план.
Пусть ЗЛП является вырожденной. Тогда у вырожденного опорного плана может быть  (но не обязательно) и поэтому может быть
(но не обязательно) и поэтому может быть  .
.
Не приведет ли это к бесконечному числу шагов? В силу конечности числа вершин множества  это может быть лишь тогда, когда через несколько шагов мы вернемся к исходному базису. Следовательно, должны встречаться цепочки
это может быть лишь тогда, когда через несколько шагов мы вернемся к исходному базису. Следовательно, должны встречаться цепочки

в которых начальное и конечное звенья совпадают, т.е.  . Такие цепочки называются циклами. Для них
. Такие цепочки называются циклами. Для них  . Но так как любые соседние опорные планы доставляют значение линейной формы
. Но так как любые соседние опорные планы доставляют значение линейной формы  , то, очевидно,
, то, очевидно,
 .
.
Таким образом, цикл означает переход от одного базиса опорного плана к другому базису того же вырожденного опорного плана. Причем, через некоторое число таких переходов имеет место возвращение к ранее встретившемуся базису. В случае образования цикла, т.е. зацикливания, всегда можно выйти из него, специальным образом выбрав «разрешающий элемент».
Методы построения начального опорного плана
Алгоритм построения начального опорного плана
Метод последовательного улучшения плана, который применяется для решения ЗЛП, предполагает знание некоторого исходного опорного плана. Однако, далеко не всегда такой начальный опорный план может быть указан без каких-либо вычислений. Это возможно лишь в случае, когда среди столбцов  матрицы условий
матрицы условий  найдётся достаточное количество таких столбцов, из которых составится единичная матрица и эта матрица будет являться базисом искомого начального плана.
найдётся достаточное количество таких столбцов, из которых составится единичная матрица и эта матрица будет являться базисом искомого начального плана.
Если же такой возможности нет, то для построения начального опорного плана ЗЛП решается вспомогательная ЗЛП (так называемая  задача) с расширенным вектором
задача) с расширенным вектором  , состоящим из вектора
, состоящим из вектора  исходной ЗЛП, дополненного искусственными неотрицательными компонентами
исходной ЗЛП, дополненного искусственными неотрицательными компонентами  . Последние вводятся в систему ограничений так, чтобы сформировался искусственный единичный базис.
. Последние вводятся в систему ограничений так, чтобы сформировался искусственный единичный базис.
Итак, начальный опорный план задачи может быть найден с помощью следующей вспомогательной ЗЛП (L – задачи):

| (11.1) |

| (11.2) |
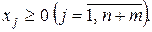
| (11.3) |
Так как матрица условий ЗЛП (11.1)-(11.3) уже содержит единичную подматрицу  которая может быть взята в качестве базиса опорного плана, то начальным опорным планом этой
которая может быть взята в качестве базиса опорного плана, то начальным опорным планом этой  задачи будет являться вектор
задачи будет являться вектор
 ,
,
у которого небазисные компоненты  а базисные
а базисные  .
.
Решая сформулированную  задачу, например, первым алгоритмом симплекс – метода, с указанным начальным планом
задачу, например, первым алгоритмом симплекс – метода, с указанным начальным планом  , в силу ограниченности линейной формы
, в силу ограниченности линейной формы  сверху на множестве своих планов (
сверху на множестве своих планов ( ) окажется, что процесс решения через конечное шагов приведет к оптимальному опорному плану вспомогательной задачи.
) окажется, что процесс решения через конечное шагов приведет к оптимальному опорному плану вспомогательной задачи.
Пусть  - оптимальный опорный план
- оптимальный опорный план  задачи, у которого все искусственные компоненты равны нулю. Тогда вектор
задачи, у которого все искусственные компоненты равны нулю. Тогда вектор  является опорным планом исходной задачи. Действительно, все дополнительные переменные
является опорным планом исходной задачи. Действительно, все дополнительные переменные 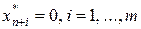 . Значит, компоненты вектора
. Значит, компоненты вектора  удовлетворяют ограничениям исходной задачи, т.е. вектор
удовлетворяют ограничениям исходной задачи, т.е. вектор  является некоторым планом исходной задачи. По построению план
является некоторым планом исходной задачи. По построению план  является также опорным.
является также опорным.






