Логіка предикатів знаходить застосування для перевірки пра вильності міркувань (і не тільки математичних), які проводяться природною мовою. Розглянемо міркування, суть яких полягає у встановлені певного логічного слідування. Перевірити коректність (правильність) такого міркування, це значить перевірити, чи логічно слідує зроблений висновок з припущень (посилок).
Отже, щоб перевірити коректність міркування (на базі логіки предикатів), яке виражене природною мовою, насамперед необхідно посилки і висновок записати символічною мовою логіки предикатів, тобто записати їх логічну структуру, а тоді розв’язати задачу на логічне слідування.
Перед тим, як розглянути конкретні приклади наведемо відому в традиційній логіці класифікацію простих категоричних суджень:
1) загальностверджувальне - «Всі P є Q»;
2) частково стверджувальне - «Деякі P є Q»;
3) загальнозаперечувальне - «Жодне P не є Q»;
4) частковозаперечувальне - «Деякі P не є Q».
Записи цих суджень мовою логіки предикатів матимуть відповідно вигляд:
1)  x (P (x) → Q (x)); (для будь-якого елемента x, якщо x має властивість P (тобто P (x) - істинне), то він також має властивість Q (тобто Q (x) - істинне); будь-який елемент x, який має властивість P, має також властивість Q);
x (P (x) → Q (x)); (для будь-якого елемента x, якщо x має властивість P (тобто P (x) - істинне), то він також має властивість Q (тобто Q (x) - істинне); будь-який елемент x, який має властивість P, має також властивість Q);
2)  x (P (x)
x (P (x)  Q (x));
Q (x));
3)  x (P (x) → ┐ Q (x));
x (P (x) → ┐ Q (x));
4)  x (P (x)
x (P (x)  ┐ Q (x)).
┐ Q (x)).
Зазначимо, що в загальних судженнях поряд з квантором загальності з’являється операція імплікації, а в часткових судженнях поряд з квантором існування - операція кон’юнкції, що відповідає змісту суджень природної мови.
відповідає змісту суджень природної мови.
Приклад 1.
Перевірити, чи правильне на базі логіки предикатів міркування:
«Деякі додатні числа менші всіх коренів рівняння f (x)=0. Жодне додатне число не менше від жодного від’ємного. Отже, жодний корінь рівняння f (x)=0 не є від’ємним».
Розв’язування.
Запишемо логічну структуру посилок і висновку, вводячи замість конкретних предикатів предикатні символи: P (x) замість «x – додатне число», Q (x) замість «x є
коренем f (x)=0», R (x, y) замість «x менше y», S (x) замість «x - від’ємне».
Тоді посилки і висновок можна подати відповідно у вигляді таких формул:
 x (P (x)
x (P (x) 
 y (Q (y) → R (x, y))),
y (Q (y) → R (x, y))),
 z (P (z) →
z (P (z) →  u (S (u) → ┐ R (z, u))),
u (S (u) → ┐ R (z, u))),
 w (Q (w) → ┐ S (w)).
w (Q (w) → ┐ S (w)).
Отже,задача звелася до перевірки співвідношення

Для перевірки логічного слідування, використаємо метод резолюції.
Спочатку посилки і заперечення висновку подамо у вигляді КНФ.Для першої посилки,тобто для формули
 x (P (x)
x (P (x) 
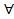 y (Q (y)
y (Q (y)  R (x, y)))
R (x, y)))
дістаємо:
 x (P (x)
x (P (x) 
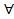 y (┐ Q (y) ˅ R (x, y)))
y (┐ Q (y) ˅ R (x, y)))
(виразили імплікацію через ┐ і ˅ );
 x
x  y (P (x)
y (P (x)  ( ┐ Q (y) ˅ R (x, y)))
( ┐ Q (y) ˅ R (x, y)))
(комутативність і пронесення квантора  y);
y);
 y (P (a)
y (P (a)  ( ┐ Q (y) ˅ R (a, y))) (1)
( ┐ Q (y) ˅ R (a, y))) (1)
(a - константа Сколема).
Аналогічні перетворення виконаємо для другої посилки:
 z (P (z)
z (P (z) 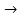
 u (S (u)
u (S (u)  ┐ R (z, u)));
┐ R (z, u)));
 z ( ┐ P (z) ˅
z ( ┐ P (z) ˅  u ( ┐ S (u) ˅┐ R (z, u)))
u ( ┐ S (u) ˅┐ R (z, u)))
(виразили  через ┐ і ˅ );
через ┐ і ˅ );
 z
z  u ( ┐ P (z) ˅┐ S (u) ˅┐ R (z, u)) (2)
u ( ┐ P (z) ˅┐ S (u) ˅┐ R (z, u)) (2)
(комутативність і пронесення квантора  u).
u).
Заперечення висновку, тобто
┐  w (Q (w)
w (Q (w)  ┐ S (w))
┐ S (w))
зведемо також до КНФ. Виконуючи перетворення, діставатимемо:
┐  w (┐ Q (w) ˅ ┐ S (w));
w (┐ Q (w) ˅ ┐ S (w));
 w ┐(┐Q (w) ˅ ┐S (w));
w ┐(┐Q (w) ˅ ┐S (w));
 w (Q (w)
w (Q (w)  S (w));
S (w));
Q (b)  S (b). (3)
S (b). (3)
В останньому виразі b - константа Сколема
Враховуючи формули (1), (2), (3), можна записати таку множину диз’юнктів:
1. P (a);
2. ┐ Q (y) ˅ R (a, y);
3. ┐ P (z) ˅ ┐ S (u) ┐ R (z, u);
4. Q (b);
5. S (b),
яку слід перевірити на суперечність.
Застосовуючи метод резолюції, дістанемо:
6. R (a, b) (4 і 2;  ={ y:= b });
={ y:= b });
7. ┐ P (a) ˅ ┐ S (b) (6 і 3;  ={ z:= a; u:= b });
={ z:= a; u:= b });
8. ┐P (a) (7 і 5);
9. □ (8 і 1)..
Порожня резольвента вказує на те, що множина суперечна, а отже, логічне слідування має місце. Значить, наведене міркування правильне.






