Упрощенный расчет камеры радиации

 

Целью этого этапа расчета является определение температуры продуктов сгорания, покидающих топку, и фактической теплонапряженности поверхности радиантных труб. Температуру (Т_п) находят методом последовательного приближения (метод итераций), используя уравнение:

, (29)

где q_p и q_pK – теплонапряженность поверхности радиантных труб (фактическая) и приходящаяся на долю свободной конвекции, ккал/м²ч;

H_p/H_S – отношение поверхностей, зависящее от типа печи, от вида и способа сжигания топлива;

Θ – средняя температура наружной стенки радиантных труб, К;

ψ – коэффициент для топок со свободным факелом ψ = 1,2; для топок с беспламенным сжиганием топлива ψ = 1,5 – 1,6; для топок с настильным факелом ψ = 1,3;

С_S = 4,96 ккал/м²чК – коэффициент лучеиспускания абсолютно черного тела.

Определение коэффициента прямой отдачи:

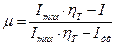, (30)

где I_max, I, I_ух – теплосодержание продуктов сгорания соответственно при температурах T_max, T_п, T_ух, рассчитывается по уравнению (11), кДж/кг;

η_Т = 0,96 – к.п.д. топки.

Суть метода расчет (метод итераций) заключается в следующем: задаются температурой продуктов сгорания (Т_п), которая находится в пределах 1000 – 1200 К; при этой температуре задаются и определяются параметры,входящие в уравнение (29).

Рассчитывают фактическую теплонапряженность радиантных труб:

(31)

Затем определяем температуру наружной стенки экрана по формуле:

, (32)

где α ₂ = 600 – 1000 ккал/м²чК – коэффициент теплоотдачи от стенки к нагреваемому продукту;

δ = 0,01 – толщина стенки трубы;

λ = 30 ккал/мчК – коэффициент теплопроводности стенки трубы;

= 0,002 – для жидких топлив.

Теплонапряженность радиантных труб, приходящаяся на долю свободной конвекции находится по формуле:

(33)

Максимальную температуру продуктов сгорания определяем по формуле:

(34)

Определим теплосодержание продуктов сгорания при максимальной температуре, кДж/кг:

(35)

По уравнению (34) получаются расчетную величину Т_п, если это значение не совпадает с заданной точностью, то расчет возобновляется, при достижении заданной точности фиксируется значение Т_п, и рассчитывается количество тепла, переданное продукту в камере радиации:

(36)

Таблица 3 – Результаты расчета Т_п методом итераций.

№	Тп зад., К	qtп, кДж/кг	Тmax, К	μ	qp, ккал/м2∙ч	Θ, К	qpk, ккал/м2∙ч	Тпрасч, К
	1100,0000	17614,8618	2194,9390	0,6729948	22289,6695	602,8713	4225,3096	1072,7017
	1072,7017	16979,9021	2200,8700	0,6910274	22886,9124	605,0114	3914,8974	1085,1558
	1085,1558	17269,1313	2198,1595	0,6828273	22615,3236	604,0382	4055,8928	1079,5476
	1079,5476	17138,7942	2199,3791	0,6865255	22737,8068	604,4771	3992,2707	1082,0880
	1082,0880	17197,8153	2198,8265	0,6848514	22682,3616	604,2785	4021,0640	1080,9403
	1080,9403	17171,1472	2199,0761	0,6856079	22707,4179	604,3682	4008,0506	1081,4594
	1081,4594	17183,2089	2198,9632	0,6852658	22696,0860	604,3276	4013,9357	1081,2247
	1081,2247	17177,7560	2199,0142	0,6854205	22701,2092	604,3460	4011,2750	1081,3308
	1081,3308	17180,2217	2198,9912	0,6853505	22698,8926	604,3377	4012,4780	1081,2829
	1081,2829	17179,1068	2199,0016	0,6853822	22699,9400	604,3415	4011,9341	1081,3046
	1081,3046	17179,6109	2198,9969	0,6853679	22699,4664	604,3398	4012,1800	1081,2947
	1081,2947	17179,3830	2198,9990	0,6853743	22699,6806	604,3405	4012,0688	1081,2992
	1081,2992	17179,4860	2198,9980	0,6853714	22699,5837	604,3402	4012,1191	1081,2972

 

Приведем расчет для последней итерации:

Принимаем Т_п = 1081,2992 К.

Теплосодержание продуктов сгорания на 1 кг топлива при заданной температуре:

Максимальная температура продуктов сгорания:

Теплосодержание продуктов сгорания при максимальной температуре:

Коэффициент прямой отдачи:

Фактическая теплонапряженность радиантных труб:

Температура наружной стенки экрана:

Теплонапряженность радиантных труб, приходящихся на долю свободной конвекции:

Расчетная температура продуктов сгорания:

Так как заданная точность достигнута, то фиксируется Т_п расч = 1081,2972 К. Рассчитывается при этой температуре количество тепла, переданное продукту в камере радиации:

где теплосодержание продуктов сгорания на 1 кг топлива при заданной температуре:

Максимальная температура продуктов сгорания:

Теплосодержание продуктов сгорания при максимальной температуре:

Коэффициент прямой отдачи:

Тогда, фактическая теплонапряженность радиантных труб:

Фактическая теплонапряженность поверхности радиантных труб меньше допустимой (23 Мкал / м ²∙ ч < 35 Мкал / м ²∙ ч), что говорит о правильно сделанном выборе типоразмера печи и эффективной ее работе.

Схема движения газовых потоков в камере радиации показана на рисунке 2.

 

 

1 – Радиантный змеевик; 2 – камера радиации; 3 – поток дымовых газов; 4 – сырьевой поток.

 

 

Рисунок 2 – Схема движения газовых потоков в камере радиации.

Расчет камеры конвекции

 

Целью данного этапа являются расчет конвекционных труб и проведение анализа эффективности работы камеры конвекции. Поставленная цель осуществляется в следующей последовательности.

Поверхность конвекционных труб определяется уравнением:

, (37)

где Q_k – количество тепла, воспринятое конвекционными трубами;

K – коэффициент теплопередачи от дымовых труб к нагреваемому продукту;

Δ t_ср – средняя разность температур;

(38)

Средняя разность температур определяется по уравнению:

, (39)

где Δ t_б = t_п – t_к; Δ t_м = t_ух – t₁ – соответственно большая и меньшая разность температур;

t_k – температура продукта на выходе из камеры конвекции, находится путем решения квадратного уравнения (21), предварительно определив теплосодержание продукта при этой температуре:

(40)

Количество тепла, воспринятое конвекционными трубами:

.

Тогда:

.

Уравнение (21) пишем в следующем виде:

, (41)

где a = 0,000405, b = 0,403

соответственно коэффициенты уравнения.

.

Решению уравнения удовлетворяет только одно значение корня:

.

.

Тогда

.

Коэффициент теплопередачи в камере конвекции рассчитывается по уравнению:

, (42)

где α ₁, α_k, α_p – соответственно коэффициенты теплоотдачи от газов к стенке, конвекцией, излучением трехатомных газов.

α_p определяют по эмпирическому уравнению Нельсона:

α_p = 0,0256∙(t_ср – 273)-2,33, (43)

где t_ср – средняя температура дымовых газов, вычисляется по формуле:

(44)

.

Тогда

α_p = 0,0256∙(782,3700 – 273)-2,33 = 10,7099 Вт/м ² К

α_k определяется следующим образом:

, (45)

где E – коэффициент, зависящий от свойств топочных газов.

.

Массовая скорость движения газов определяется по формуле:

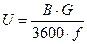, (46)

где f – свободное сечение прохода дымовых газов в камере конвекции, которое определяется по уравнению.

(47)

где n – число труб в одном горизонтальном ряду, S ₁ – расстояние между осями труб в горизонтальном ряду, определено ранее; α – характерный размер для камеры конвекции; d – наружный диаметр труб; l_p – рабочая длина конвекционных труб.

(48)

.

.

Тогда:

.

.

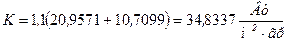Определяем число труб в камере конвекции:

(49)

где .

.

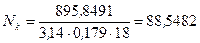Принимаем: N_k = 92.

Число труб по вертикали:

(50)

.

Высота пучка труб в камере конвекции:

(51)

где S2 – расстояние между горизонтальными рядами труб, которое определяется как:

(52)

.

Определяем среднюю теплонапряженность:

(53)

.

Схема расположения труб и газовые потоки в камере конвекции показана на рисунке 3.

 

 

 

 

Рисунок 3 – схема расположения труб и газовые потоки в камере конвекции.