Согласованный фильтр обеспечивает при флуктуационной помехе в канале типа «белого шума», в момент окончания сигнала t 0 = Т с, на своём выходе максимально возможное отношение пиковой мощности сигнала к мощности помехи. Выигрыш в отношении сигнал/шум на выходе СФ по сравнению со входом равняется базе сигнала (В = 2 ·F с ·Т с), т. е.
 ,
,
где Тс = N×Т – длительность сигнала (N - число элементов в дискретной последовательности);
 – ширина спектра сигнала.
– ширина спектра сигнала.
Таким образом, выигрыш q = (hвых)2 / (hвх)2, обеспечиваемый СФ при приёме дискретных последовательностей, составляет N раз. Следовательно, путём увеличения длины дискретных последовательностей, отображающих символы сообщений ²1² и ²0², можно обеспечить значительное повышение отношения сигнал/шум на входе решающей схемы приёмника и, соответственно, повышение помехоустойчивости передачи дискретных сообщений. Очевидно, что это будет приводить к снижению скорости передачи сообщений.
При приеме сложного сигнала оптимальным фильтром действует метод накопления, в результате чего энергетический выигрыш равен:
 ;
;
где N – количество элементарных сигналов в сложном сигнале.
hсогл2 = N*h2 = 11* 2,22; hсогл = 5;
Энергетический выигрыш достигается ценой уменьшения скорости передачи информации.
18.Вероятность ошибки на выходе приемника при применении сложных сигналов и согласованного фильтра.
При определении вероятности ошибки считаем, что сигналы, соответствующие символам "1" и "0", являются взаимно противоположными и решение о переданном символе принимается с использованием пороговой решающей схемы синхронным способом, (отсчеты берутся в конце каждого сигнала длительностью kT, где T - длительность одного элемента сложного сигнала). При этом считаем, что длительность сигнала возросла в k раз по сравнению со случаями использования простых сигналов, где k - количество элементарных посылок в сложном сигнале.
Для определения вероятности ошибки на выходе при применении согласованного фильтра воспользуемся формулой:

19. Пропускная способность разработанной системы связи.
Информация, переданная за несколько отсчетов максимальна в том случае, когда отсчеты сигналов независимы. Этого можно достичь, если сигнал выбрать так, чтобы его спектральная плотность была равномерной в полосе F. Отсчеты, разделенные интервалами, кратными 1/2F, взаимно некоррелированы, а для гауссовских величин некоррелированность означает независимость. Поэтому пропускную способность С можно найти:
С=F 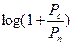
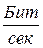
Где Pс –мощность сигнала, Рш – мощность шума.
Рс=Ес / Т=(А*А*Т)/(2*Т)=А*А/ 2.
Рш равна дисперсии шума.
F пр ДЧМ =2,5/Т.
Откуда получаем конечное значение для пропускной способности разработанной системы связи.
Заключение
Современная теория электросвязи позволяет достаточно полно оценить различные системы связи по их помехоустойчивости и эффективности и тем самым определить какие из этих систем являются наиболее перспективными
Теория достаточно четко указывает не только возможности совершенствования существующих систем связи, но и пути создания новых более современных систем.
Приложение. Расчет исходных данных для заданного варианта работы.
K=1,4;
M=8;
N=12;
Г=9
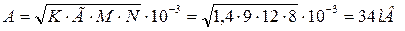

p(1)=9/12=0,75
Z(t0)=(0,25+σ)A=(0,25+  =9 мВ
=9 мВ
Z(t1)= Z(t0)=9 мВ
Z(t2)= 0,6 Z(t0)=5,4 мВ
Z(t3)= 1,1 Z(t0)=9,9 мВ
 Бод
Бод

bmax=2+0,3N=2+0,3·12=5,6 В
П=1,5+0,1N=1,5+0,1·12=2,7.
(2541)8=(10.101.100.001)2
| S1(t) | -1 | -1 | -1 | -1 | -1 | -1 | |||||
| S2(t) | -1 | -1 | -1 | -1 | -1 |
СПИСОК ЛИТЕРАТУРЫ.
1. Теория передачи сигналов: Учебник для вузов / А. Г. Зюко, Д. Д. Кловский
2. Макаров А.А., Чиненков Л.А. Основы теории помехоустойчивости дискретных сигналов: Учеб. пособие.—Новосибирск, СибГАТИ, 1997.—42 с.
3. Макаров А.А. Методы повышения помехоустойчивости систем связи.—Новосибирск, СИИС, 1991.—58 с.
4. Конспект лекций.






