СПРАВОЧНЫЙ МАТЕРИАЛ
ДЛЯ ПОДГОТОВКИ К ИНТЕРНЕТ-ТЕСТИРОВАНИЮ
ПО КУРСУ «МАТЕМАТИКА»
Методические указания для студентов 2-3-го курсов
всех специальностей очной формы обучения
Ростов-на-Дону
Составители: кандидат физико-математических наук, профессор Соболев В.В.,
кандидат физико-математических наук, доцент Нурутдинова И.Н.
УДК 51
Справочный материал для подготовки к Интернет-
тестированию по курсу «Математика»: Метод. указания
Для студентов 2-3-го курсов всех специальностей очной
формы обучения / РГАСХМ ГОУ,
Ростов н/Д, 2007. — 22 с.
Предназначены для подготовки к централизованному Интернет-тестированию по завершении курса «Математика». В краткой форме приводятся важнейшие теоретические положения, определения, правила, алгоритмы и формулы из основного курса «Математика» («Высшая математика») для всех специальностей.
Предназначено для студентов 2-3-го курсов всех специальностей очной формы обучения.
Печатается по решению Редакционно-издательского совета академии
Рецензент кандидат физико-математических наук, доцент В.В.Трепачёв
Научный редактор кандидат физико-математических наук, профессор В.В.Соболев
© Государственное образовательное учреждение
высшего профессионального образования
Ростовская-на-Дону государственная академия
сельскохозяйственного машиностроения, 2007
СОДЕРЖАНИЕ
ВВЕДЕНИЕ..................................... 3
1. Комплексные числа..................................... 4
2. Матрицы и системы линейных алгебраических уравнений (СЛАУ)..... 5
3. Векторная алгебра..................................... 5
4. Аналитическая геометрия................................. 6
5. Теория пределов. Дифференциальное исчисление................. 8
6. Интегральное исчисление.................................10
7. Дифференциальные уравнения..............................11
8. Ряды.............................................. 12
9. Теория вероятностей....................................14
10. Математическая статистика.............................. 17
11. Математические модели в экономике........................ 19
ЛИТЕРАТУРА........................................ 21
ВВЕДЕНИЕ
Справочный материал составлен с учётом того, что студенты изучили курс «Математика» («Высшая математика») в соответствии с Государственными образовательными стандартами и владеют необходимой математической символикой.
Цель данной методической разработки — помочь студентам обновить в памяти, обобщить и закрепить знания, полученные при изучении курса высшей математики перед прохождением централизованного Интернет-тестирования. Она будет полезна также для успешного дальнейшего обучения в академии по дисциплинам естественнонаучного цикла и специальным дисциплинам, читаемым на профилирующих кафедрах.
Дано сжатое изложение важнейших математических понятий, определений, правил и алгоритмов решения задач, наиболее употребительных формул, необходимых при решении основных задач, включённых в программу тестирования. При этом авторы ориентировались на базу тестовых заданий, предлагавшихся Федеральным Центром тестирования на репетиционных и итоговых тестированиях 2005 — 2006 г.г.
Программы тестирования для разных специальностей различны. Данное методическое указание содержит материал для всех специальностей, как технических, так и экономических. В связи с этим некоторые разделы пособия являются избыточными для отдельных специальностей. Так, например, в разделе 11 «Математические модели экономики» представлен справочный материал, необходимый лишь для студентов специальностей 080502 («Экономика и управление на машиностроительном предприятии») и 080507 («Менеджмент организации»). Раздел 8 «Ряды» необязателен для студентов специальностей 220201 («Управление и информатика в технологических системах») и 230201 («Информационные системы и технологии»). Остальные разделы содержат материал в большей или меньшей степени необходимый для всех специальностей.
При подготовке к централизованному тестированию в режиме on-line рекомендуется пройти индивидуально репетиционное тестирование, демоверсии которого для всех специальностей можно найти на сайте www.fepo.ru.
Комплексные числа
 ;
;  ,
,  .
.
 ;
;  .
.
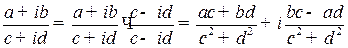 .
.
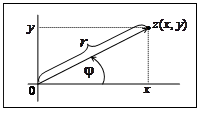
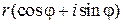 — тригонометрическая форма;
— тригонометрическая форма;

 ;
;  ;
;
 ;
;

 ;
;

 .
.
2. Матрицы и системы линейных алгебраических уравнений (СЛАУ)
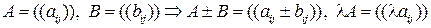 .
.
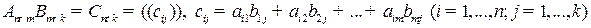 .
.
 ;
;  .
.
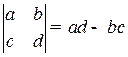 ;
;  .
.
Правило Крамера решения СЛАУ вида  :
:
 .
.
Образ  вектора
вектора  при линейном отображении
при линейном отображении
с матрицей  :
:
 .
.
3.Векторная алгебра
 ;
;  ;
;  ;
;
 ;
;  .
.
Скалярное произведение:  ;
;

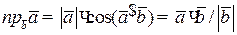 ;
; 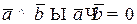 .
.
Векторное произведение: 

 .
.
Смешанное произведение:  .
.

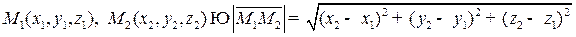 .
.
Аналитическая геометрия
 Уравнение плоскости
Уравнение плоскости  :
: 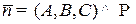 ;
;  — нормальный вектор;
— нормальный вектор;
 ;
;  .
.
 Уравнения прямой l в пространстве:
Уравнения прямой l в пространстве: 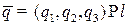 ;
;
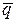 — направляющий вектор;
— направляющий вектор;
канонические: 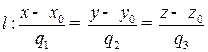 ;
;  ;
;  ;
;
параметрические:  .
.
Канонические уравнения прямой l в пространстве, проходящей через точку  и перпендикулярной к плоскости
и перпендикулярной к плоскости  :
:
 .
.
Уравнение прямой l на плоскости xOy:  ;
; 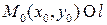 ;
;

 ;
;  ;
;  .
.
 ;
; 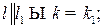



Уравнение прямой l, проходящей через две точки  :
:
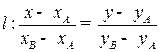 ;
;  ;
;  — угловой коэффициент.
— угловой коэффициент.
Координаты середины С отрезка  ,
,  :
:
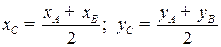 .
.
Уравнения кривых 2-го порядка:
Окружность:  ;
; 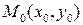 — центр, R — радиус.
— центр, R — радиус.
Эллипс:  ;
;  — центр, а, b — полуоси.
— центр, а, b — полуоси.
Гипербола: 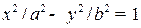 ;
;  — центр,
— центр,
а — действительная, b — мнимая полуоси.
Парабола:  ;
;  — вершина, ось абсцисс Ох — ось симметрии.
— вершина, ось абсцисс Ох — ось симметрии.
Уравнения поверхностей 2-го порядка:
Сфера:  ;
;  — центр,
— центр,
R — радиус.
Эллипсоид:  ;
;  — центр, а, b, c — полуоси.
— центр, а, b, c — полуоси.
Гиперболоиды: однополостный:  ;
;
двуполостный: 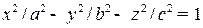 .
.
Параболоиды: эллиптический:  ;
;
гиперболический: 
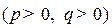 .
.
 Цилиндрические поверхности (образующая — ось Oz):
Цилиндрические поверхности (образующая — ось Oz):
 — эллиптический цилиндр;
— эллиптический цилиндр;
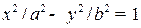 — гиперболический цилиндр;
— гиперболический цилиндр;
 — параболический цилиндр.
— параболический цилиндр.
Конус 2-го порядка:  .
.
Теория пределов. Дифференциальное исчисление
 -окрестность точки а: промежуток
-окрестность точки а: промежуток  ,
,  .
.

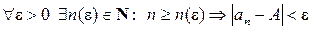 .
.

 .
.
Функция  непрерывна в точке
непрерывна в точке  , если
, если  .
.
 ,
,
 т. е.
т. е.  .
.

 .
.
 ;
; 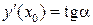 .
.
Уравнения касательной  ,
,
нормали  если
если 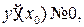
или  , если
, если 
 ;
;
 .
.
 ;
; 



 ;
; 
 ;
; 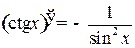 ;
;
 ;
; 
 .
.
Необходимое условие экстремума:  — т. экстремума и
— т. экстремума и 
 .
.
 Достаточные условия экстремума:
Достаточные условия экстремума:
 ;
; 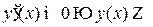 ;
;  .
.
 ;
;  .
.
Правило Лопиталя: 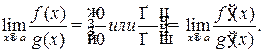
 — закон движения точки по прямой
— закон движения точки по прямой 
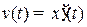 — скорость,
— скорость,
 — ускорение.
— ускорение.
 — закон движения точки в пространстве
— закон движения точки в пространстве 
 — вектор скорости,
— вектор скорости,
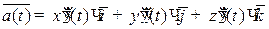 — вектор ускорения.
— вектор ускорения.
Нахождение наибольшего и наименьшего значений непрерывной функции  на отрезке
на отрезке  :
:
а) найти внутри  все критические точки функции, т. е. такие, что
все критические точки функции, т. е. такие, что  или
или  не существует;
не существует;
б) вычислить  ,
,  и значения
и значения  во всех критических точках;
во всех критических точках;
в) выбрать наибольшее и наименьшее значения.
Образ отрезка  при отображении непрерывной функцией
при отображении непрерывной функцией  — отрезок
— отрезок  , где с — наименьшее, d — наибольшее значения
, где с — наименьшее, d — наибольшее значения  на
на  .
.
Формула Тейлора  :
:

Формула Маклорена:
 .
.
Частные производные:  ;
;
 .
.
 — градиент скалярного поля
— градиент скалярного поля  .
.
 — производная
— производная
скалярного поля в направлении единичного вектора  ,
,
 — углы, образованные вектором
— углы, образованные вектором  с ортами
с ортами 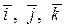 .
.
Условия дифференцируемости функции комплексного переменного  в точке
в точке  :
:  .
.
Метод Лагранжа решения задачи на условный (относительный) экстремум функции 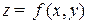 при условии
при условии 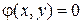 :
:
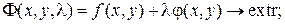
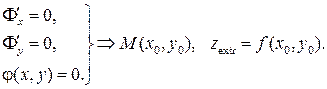
6. Интегральное исчисление
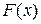 — первообразная для
— первообразная для  , если
, если  ;
; 


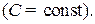

 ;
;


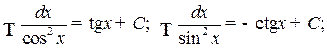
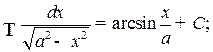




 .
.
 ;
;
 .
.
7. Дифференциальные уравнения (ДУ)
Решение ДУ — дифференцируемая функция, обращающая ДУ в верное тождество.
Порядок ДУ — порядок старшей производной (старшего дифференциала) в данном уравнении.
Задача Коши для ДУ 1-го порядка вида  : найти частное решение ДУ, удовлетворяющее условию
: найти частное решение ДУ, удовлетворяющее условию  , где
, где  — заданные числа.
— заданные числа.
Типы ДУ 1-го порядка:
а) с разделяющимися переменными: 
или  (решается разделением переменных:
(решается разделением переменных:  …);
…);
б) однородное (в однородных функциях):  или
или  , где
, где 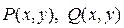 — однородные функции одинаковой степени однородности (решается заменой
— однородные функции одинаковой степени однородности (решается заменой 
 );
);
 в) линейное неоднородное:
в) линейное неоднородное: 
г) типа Бернулли: 
(решаются методом Бернулли сведением к двум ДУ с разделяющимися
переменными для функций  :
:  …).
…).
Линейное ДУ 2-го порядка с постоянными коэффициентами:
 (однородное, если
(однородное, если 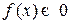 , и неоднородное, если
, и неоднородное, если  ).
).
Общее решение неоднородного ДУ:  , где
, где  — общее решение однородного,
— общее решение однородного,  — какое-либо частное решение неоднородного ДУ.
— какое-либо частное решение неоднородного ДУ.
Решение однородного ДУ: составляется характеристическое уравнение  ;
;
а) корни  — действительные,
— действительные, 

 ;
;
б) корни  — действительные,
— действительные, 

 ;
;
в) корни  — комплексно сопряжённые
— комплексно сопряжённые 
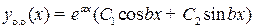 .
.
Решение линейного неоднородного ДУ методом подбора: если  — многочлен от х степени m, то
— многочлен от х степени m, то  , где
, где  — многочлен степени m с неопределёнными коэффициентами,
— многочлен степени m с неопределёнными коэффициентами,  — кратность корня
— кратность корня  характеристического уравнения.
характеристического уравнения.
Ряды
Ряд  сходится, если
сходится, если  где
где  ;
;
 — сумма ряда.
— сумма ряда.
Ряд  сходится
сходится 
 ;
; 
 ряд
ряд  расходится.
расходится.
 .
.
 расходится.
расходится.
 .
.
Признаки сравнения положительных рядов:
1) при  :
:
а)  ;
;
б)  .
.
2) 

 (эквивалентны).
(эквивалентны).
Признаки сходимости положительных рядов  :
:
1 ) Даламбера: 
2) Радикальный признак Коши: 
Условия сходимости знакопеременных рядов:
 сходится
сходится 
 сходится абсолютно;
сходится абсолютно;
 сходится, а
сходится, а  расходится
расходится 
 сходится условно.
сходится условно.
Признак Лейбница сходимости знакочередующегося ряда  ,
,
 : если
: если  и
и 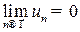 , то ряд
, то ряд  сходится,
сходится,  .
.
Степенной ряд 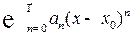 : интервалсходимости
: интервалсходимости  ,
,
радиус сходимости 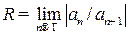 или
или  .
.
Степенные разложения:
а )  ; б )
; б )  ;
;
в )  ;
;
г)  .
.
Гармонические колебания: простая гармоника  или
или  , где
, где  — амплитуда,
— амплитуда,  — частота,
— частота,  — начальная фаза.
— начальная фаза.
Ряд Фурье для функции  с периодом
с периодом  , заданной на
, заданной на  :
:
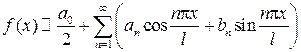 ,
,
 , n= 1,2,…
, n= 1,2,…
Ряд Фурье для функции  , заданной на
, заданной на 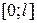 :
:
 а) по косинусам (
а) по косинусам ( — чётная функция,
— чётная функция, 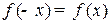 ):
):
 ;
;  ;
;
 б) по синусам (
б) по синусам ( — нечётная функция,
— нечётная функция,  ):
):
 ;
; 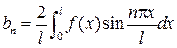 .
.
Теория вероятностей
Элементы комбинаторики:
Число перестановок (упорядоченных комбинаций) изnэлементов:  .
.
Число сочетаний (неупорядоченных комбинаций) изnэлементов по m:

Число размещений (упорядоченных комбинаций) изnэлементов по m:
 .
.
Сумма событий  — наступление хотя бы одного из событий
— наступление хотя бы одного из событий 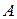 или
или  .
.
Произведение событий  — наступление обоих событий
— наступление обоих событий 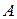 и
и  .
.
 ;
;
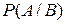 — условная вероятность события
— условная вероятность события 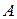 при условии, что событие
при условии, что событие  произошло в данном опыте.
произошло в данном опыте.
Классическая вероятность:  ,
, 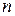 — число всех случаев полной группы попарно несовместимых, равновозможных исходов опыта,
— число всех случаев полной группы попарно несовместимых, равновозможных исходов опыта, 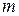 — число случаев, благоприятствующих событию А.
— число случаев, благоприятствующих событию А.
Геометрическая вероятность:  ,
, 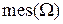 — мера (длина, площадь или объём) бесконечного множества
— мера (длина, площадь или объём) бесконечного множества  всех элементарных исходов,
всех элементарных исходов,  — мера подмножества всех элементарных исходов из
— мера подмножества всех элементарных исходов из  , благоприятствующих событию А. Используется при равномерном распределении по
, благоприятствующих событию А. Используется при равномерном распределении по  вероятностей событий, прямо пропорциональных мере подмножеств благоприятствующих исходов.
вероятностей событий, прямо пропорциональных мере подмножеств благоприятствующих исходов.
Теорема сложения:  .
.
Теорема умножения:  .
.
А не зависит от В (т. е. 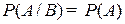 )
)  .
.
Формула Бернулли: 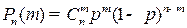 ;
;  ;
;
 ;
;  — наивероятнейшее (модальное) значение числа появления события A в серии из
— наивероятнейшее (модальное) значение числа появления события A в серии из 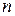 независимых испытаний в схеме Бернулли,
независимых испытаний в схеме Бернулли,  — вероятность появления A в каждом отдельном испытании.
— вероятность появления A в каждом отдельном испытании.
Формула полной вероятности:
 ,
,  — гипотезы
— гипотезы
( — достоверно,
— достоверно,  — невозможно,
— невозможно,  ).
).
Функция распределения (интегральная) случайной величины (СВ) X:
 .
.
Функция плотности вероятности:  ;
;
 ;
;  .
.
Математическое ожидание (среднее значение) СВ Х:
а) Х — дискретная СВ:  ;
;
б) Х — непрерывная СВ:  .
.
Дисперсия СВ Х:  ;
;
а) Х — дискретная СВ:  ;
;
б) Х — непрерывная СВ:
 .
.
Среднеквадратическое отклонение СВ Х:  .
.
Математическое ожидание функции  дискретной СВ Х:
дискретной СВ Х:
 .
.
Закон Бернулли (биномиальный):  ;
;
 ;
;
 ;
;  ,
,  ;
; 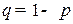 .
.
Закон Пуассона:  ;
;  ;
; 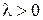 ;
;
 .
.
Равномерный закон:


 ;
;  .
.
Показательный закон:  .
.
Нормальный закон Гаусса:  ;
;
 .
.
Математическая статистика
Х — изучаемая СВ (признак), 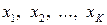 — её различные наблюдаемые
— её различные наблюдаемые
значения (варианты), встречающиеся соответственно 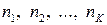 раз в выборке объёма
раз в выборке объёма  из генеральной совокупности;
из генеральной совокупности;  — частота (абсолютная),
— частота (абсолютная),  относительная частота варианты
относительная частота варианты  ,
,  — число различных вариант выборки.
— число различных вариант выборки.
 Статистический ряд:
Статистический ряд:
 или
или 
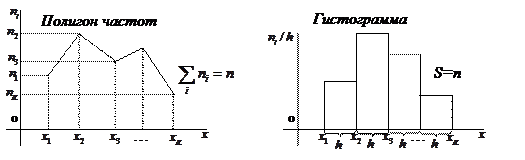
Мода вариационного ряда —варианта, имеющая максимальную частоту.
Выборочные (точечные) оценки параметров распределения признака
в генеральной совокупности:
а) выборочная средняя (несмещённая оценка генеральной средней М (X)):
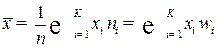 ;
;
б) выборочна дисперсия (смещённая оценка D (X)):
 ;
;
в) исправленная выборочная дисперсия (несмещённая оценка D (X)):
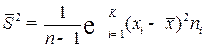 или
или  ;
;
г) исправленная выборочная оценка среднеквадратического отклонения (несмещённая оценка  ):
):  или
или  .
.
Парная регрессия:  — две СВ,
— две СВ,  — выборка, содержащая
— выборка, содержащая 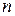 пар значений признаков
пар значений признаков  .
.
Линейная регрессия  на
на  :
:  или
или  — приближённое представление статистической зависимости
— приближённое представление статистической зависимости  от
от  (в форме линейной зависимости),
(в форме линейной зависимости),  — коэффициент регрессии,
— коэффициент регрессии,
где  ,
,  — средние выборочные значения,
— средние выборочные значения,
 — выборочные оценки
— выборочные оценки 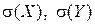 ,
,  — выборочный коэффициент корреляции,
— выборочный коэффициент корреляции, 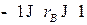 ;
;
 ;
;
 — мера тесноты линейной корреляционной зависимости СВ
— мера тесноты линейной корреляционной зависимости СВ  и
и  ;
;
 (прямая зависимость
(прямая зависимость  от
от  );
);
 (обратная зависимость
(обратная зависимость  от
от  ).
).
Оценки параметров:
а) точечная (определяется одним числом);
б) интервальная (определяется концами интервала 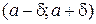 , симметричного относительно точечной оценки
, симметричного относительно точечной оценки  , покрывающего с определённым уровнем надёжности точное неизвестноезначение параметра распределения генеральной совокупности).
, покрывающего с определённым уровнем надёжности точное неизвестноезначение параметра распределения генеральной совокупности).
Статистическая гипотеза — гипотеза о виде (законе) неизвестного распределения или о параметрах известного распределения признака в генеральной совокупности.
Выдвинутая гипотеза называется нулевой и обозначается  . Гипотеза, противоположная нулевой, называется конкурирующей и обозначается
. Гипотеза, противоположная нулевой, называется конкурирующей и обозначается 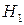 .
.
Ошибка первого рода — отвергается нулевая гипотеза, когда она на самом деле является верной. Вероятность совершить ошибку первого рода называется уровнем значимости.
Ошибка второго рода — принимается нулевая гипотеза, когда на самом деле является верной конкурирующая гипотеза.






