Системы счисления
Понятие системы счисления
Системы счисления (c/c) делятся на позиционные и непозиционные. В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы. Сама же запись числа 757,7 означает сокращенную запись выражения 700 + 50 + 7 + 0,7 = 7 ∙ 102 + 5 ∙ 101 + 7 ∙100 + 7 ∙ 10–1 = 757,7.
Основание позиционной c/c – это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание системы можно принять любое натуральное число. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения an –1∙ qn –1 + an –2∙ qn –2 +... + a 1∙ q 1 + a 0∙ q 0 + a –1∙ q –1 +... + a – m ∙ q – m , где n и m – число целых и дробных разрядов, соответственно.
Основание с/с соответствует количеству цифр (знаков), используемых для записи чисел в этой с/с. Например, основанием десятичной с/с есть число 10, и только десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) используются при записи чисел в этой с/с. В двоичной с/с используются две цифры – 0 и 1, в шестнадцатеричной – 16, причем для чисел 10, 11, 12, 13, 14, 15 в этой с/с введены дополнительные цифры (знаки) – A, B, C, D, E, F, соответственно, т.к. традиционно используемых цифр недостаточно.
Основание 10 не слишком удобно (в цепях электрических схем необходимо для этого иметь 10 различных сигналов). С технической точки зрения, чем меньше сигналов в схеме, тем лучше. Наименьшее основание, которое может быть у позиционной с/с, – это 2. Поэтому двоичная с/с широко используется в современной вычислительной технике, в устройствах автоматики и связи.
Кроме десятичной с/с для «общения с компьютером» широко используются системы с основанием, являющимся целой степенью числа 2, а именно двоичная, восьмеричная и шестнадцатеричная.
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел (табл. 1.1).
Таблица 1.1
Представление чисел в с/с
| Десятичная с/c | Двоичная с/c | Восьмеричая с/c | Шестнадцатиричная с/c |
| А | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Как видно из таблицы, недостатком 2 с/с является быстрый рост числа разрядов, необходимых для записи чисел. В восьмеричной и шестнадцатеричной с/c требуется соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).
Перевод чисел
Перевод из 8-й и 16-й в 2-ю с/c
Для перевода достаточно каждую цифру числа заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Пример
502(8 c/c) →? (2 c/c)
502(8 c/c) = 101000010 (2 c/c)
Перевод из 2-й с/c в 8-ю и 16-ю
Для перевода нужно разбить число влево и вправо от последнего разряда (или запятой) на триады или тетрады и каждую такую группу заменить соответствующей восьмеричной или шестнадцатеричной цифрой. В случае необходимости неполные триады дополняются нулями.
Пример
1111110(2 c/c) →? (8 c/c)
1111110 (2 c/c) = 001111110 (2 c/c) = 176(8 c/c)
1111010101,1100(2 c/c) →? (16 c/c)
001111010101, 1100 (2 c/c) = 3D5,C(16 c/c).
Перевод из произвольной с/с в 10-ю и наоборот
Пусть имеется с/с с основанием k и некоторое число a 1 ...an в этой с/с, где a 1,..., an – цифры этого числа. Данное число можно представить в виде: a 1 ∙ kn –1 +a 2 ∙ kn – 2 +...+an ∙ k 0.
Пример
110011(2 c/c) →? (10c/c)
110011(2 c/c) = 1 ∙ 10101+1 ∙ 10100+0 ∙ 1011+0 ∙ 1010+1 ∙ 101+1 ∙ 100(2 c/c)=
=1∙ 25+1∙ 24+0∙ 23+0∙ 22+1∙ 21+1∙ 20 (10 c/c)= 32 + 16 + 2 + 1 = 51(10 c/c),
1216,04(8 c/c) →? (10 c/c)
1216,04(8 c/c) = 1 ∙ 83 + 2 ∙ 82 + 1 ∙ 81 + 6 ∙ 80+4 ∙ 8–2= 512 + 128 + 8 + 6 + 0,0625 = 654,0625(10 c/c).
Перевод из 10 с/c в произвольную
Данный алгоритм является обратным к алгоритму, рассмотренному выше. Исходное число делится на основание с/с, в которую требуется перевести число. Первый шаг: разделить исходное число на r (основание новой с/c), зафиксировать остаток от деления (число от 0 до r – 1) и частное. Второй шаг: если частное больше r, то снова разделить его на r, продолжая фиксировать остаток от деления. Процесс деления частных продолжать до тех пор, пока частное не станет меньше r. Третий шаг: все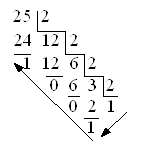 
полученные в процессе деления остатки от деления и последнее частное будут образовывать цифры исходного числа в с/с с основанием r. Выписав все найденные цифры в обратном порядке (начиная с последнего частного), получим искомое представление числа в новой с/c.
Например, требуется 25(10 c/c) перевести в 2-ю с/c. Согласно алгоритму, получаем 11001(2 c/c). Проверим результат:
25(10 c/c) = 11001(2 c/c) = 1 ∙ 24 + 1 ∙ 23 + 0 ∙ 22 + 0 ∙ 21 + 1 ∙ 20 = 25(10 c/c).
Перевод дробной части числа
Чтобы правильную дробь перевести из с/c с основанием r в c/c с основанием q необходимо последовательно умножать дробную часть (сначала самого числа, а потом получающихся произведений) на новое основание с/c q до тех пор, пока: либо дробная часть получаемого произведения не станет равна нулю; либо не будет достигнута нужная точность (заданное число цифр после запятой). В новой с/c число запишется в виде последовательности целых частей получаемых произведений, начиная с первого. Важнопомнить, что все действия производятся в исходной с/c.
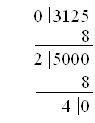Пример
0,3125(10 c/c) →? (8 c/c)
0,3125(10 c/c) = 0,24(8 c/c)
При переводе смешанной дроби из одной с/с в другую, отдельно по своим правилам, переводится целая часть и отдельно дробная, а результаты затем приписываются друг к другу через точку.
