Расчет однофазных линейных цепей переменного тока

Расчет линейных электрических цепей постоянного тока

Задание

Для электрической цепи (рис.1.1) выполнить следующее:

1 Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

2 Определить токи во всех ветвях схемы, используя метод контурных токов;

3 Определить токи во всех ветвях схемы на основании метода наложения

4 Составить баланс мощностей для заданной схемы;

5 Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить

6 Определить ток во второй ветви методом эквивалентного генератора;

7 Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

Дано: =20 B, 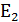=30 B, =64 Ом, =43 Ом, =31 Ом, =25 Ом, =52, Ом, =14 Ом, =1 Ом, =2 Ом.

Определить: , , , ,

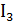Схема цепи изображена на рис. 1.1.

Лист

Решение

1) Составляем на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях цепи, используя схему на рис. 1.1.

Заданная цепь имеет пять неизвестных токов, значит, система должна иметь пять независимых уравнений. По первому закону Кирхгофа составляем 2 независимых уравнения. Выбираем узлы C и D. По второму закону Кирхгофа нам остается составить три контурных уравнения, чтобы общее количество уравнений было равно количеству неизвестных токов, то есть пяти. Выбираем контуры I, II и III. Таким образом, система уравнений имеет вид:

Узел A I₁+I₃−I₄=0;

Узел B −I₂ +I₄+I₅=0;

Контур I I₁(R₀₁+R₁)−I₃(R₃+R₆)=E₁;

Контур II I₁(R₀₁+R₁)+I₄R₄+I₂(R₂+R₀₂)=E₁+E₂;

Контур III I₂(R₂+R₀₂)+I₅R₅=E₂.

 

2) Определяем токи во всех ветвях, используя метод контурных токов. Выбираем независимые контуры I, II и III, намечаем в них контурные токи I_K1, I_K2 и I­_K3 , как показано на рисунке 1.1 и составляем систему уравнений по второму закону Кирхгофа для данной системы контурных токов:

Лист

I_K1(R₀₁+R₁+R₃+R₆)+I_К2(R₀₁+R₁)=E₁;

I_K1(R₀₁+R₁)+I_K2(R₀₁+R₁+R₀₂+R₂+R₄)+I_К3(R₀₂+R₂)=E₂+E₁;

I_К2(R₀₂+R₂)+I_K3(R₂+R₀₂+R₅)=E₂;

 

Подставляем числовые значения параметров в систему уравнений:

I_K1(1+64+31+14)+I_К2(1+64)=20;

I_К1(1+64)+I_K2(1+64+43+2+25)+I_K3(2+43)=30+20;

I_K2(2+43)+I_K3(43+2+52)=30.

 

I_K1110+ I_K265 =20;

I_K165+ I_K2135+ I_K345=50;

I_K245+ I_K397=30.

С помощью SN−калькулятора рассчитываем определители.

Определитель системы

;

 

Частные определители

 

 

 

 

 

Определяем контурные токи:

 

Лист

I_K1= = =−0,0076 A;

 

I_K2= = 0,32 A;

 

I_K3= 0,1606 A.

Определяем действительные токи в ветвях:

I₁=I_K1+I_K2=−0,0076+0,32=0,3124 A;

I₂=I_K2+I_K3=0,32+0,1606=0,4806 А;

I₃=−I_K1=0,0076 А;

I₄=I_K2=0,32 A;

I₅= I_K3=0,1606 А.

 

3) Определяем токи в ветвях цепи по методу наложения, при котором ток на любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.

 

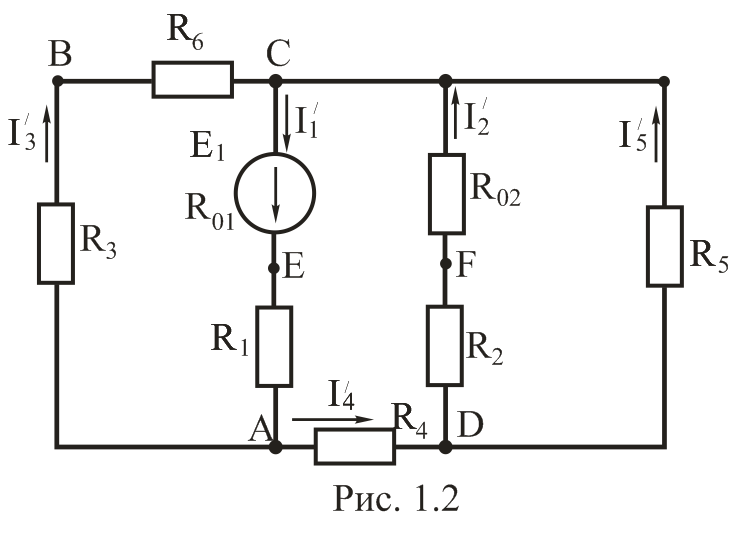
а) Определяем частные токи от ЭДС Е₁, при отсутствии ЭДС Е₂, то есть рассчитываем цепь по схеме рис. 1.2.

Лист

Показываем направление частных токов от ЭДС Е₁ и обозначаем токи с одним штрихом: I₁^/ и т. д. Решаем задачу методом «свертывания».

Определяем эквивалентные сопротивления участков и всей цепи:

R_1.01=R₁+R₀₁ =64+1=65Ом;

R_2.02=R₂+R₀₂ =43+2=45 Ом.

R₃₆=R₃+R₆ =31+14=45 Ом.

R_2.02.5 = R_2.02∙R₅/(R_2.02+R₅)= 45∙52/(45+52)=24,1 Ом;

R_2.02.54= R_2.02.5+R₄=24,1+25=49,1 Ом;

R_2.02.3456= R₃₆∙R_2.02.54/(R₃₆+R_2.02.54)=45∙49,1/(45+49,1)=23,5 Ом;

R_э= R_2.02.3456+ R_1.01=23,5+65=88,5 Ом.

Применяя законы Ома, Кирхгофа и формулу разброса, вычисляем токи ветвей:

I₁^/= 0,226 А;

I₃^/= I₁^/ 0,1179А;

I₄^/= I₁^/– I₃^/= 0,226– 0,1179=0,1081 А.

I₂^/=I₄^/ 0,058 А;

I₅^/= I₃^/– I₂^/= 0,1081–0,058=0,0501 А.

б)Определяем частные токи от ЭДС Е₂ при отсутствии ЭДС Е₁, т.е. рассчитываем цепь по рис. 1.3.

Лист

 

Определяем эквивалентные сопротивления участков и всей цепи:

R_1.01=R₁+R₀₁ =64+1=65Ом;

R_2.02=R₂+R₀₂ =43+2=45 Ом.

R₃₆=R₃+R₆ =31+14=45 Ом.

R_1.01.36 = R_1.01∙R₃₆/(R_1.01+R₃₆)= 65∙45/(65+45)=26,6 Ом;

R_1.01.346= R₄+R_1.01.36=25+26,6=51,6 Ом;

R_1.01.3456= R₅∙R_1.01.346/(R₅+R_1.01.346)=52∙51,6/(52+51,6)=25,9 Ом;

R_э= R_1.01.3456+ R_2.02=25,9+45=70,9 Ом.

Применяя законы Ома, Кирхгофа и формулу разброса, вычисляем токи ветвей:

I₂^//= 0,4231 А;

I₄^//= I₂^// 0,2124А;

I₅^//= I₂^//– I₄^//= 0,4231– 0,2124=0,2107 А.

I₁^//= I₄^// 0,0869 А;

I₃^//= I₄^//– I₁^//= 0,2124– 0,0869=0,1255 А.

 

 

Лист

Определяем действительные токи в цепи:

I₁=I₁^/+I₁^//=0,226+0,0869=0,3129 А;

I₂= I₂^/+I₂^//=0,058+0,4231=0,4811 А;

I₃=I₃^//−I₃^/=0,1255−0,1179=0,0076 А;

I₄=I₄^/+I₄^//=0,1081+0,2124=0,3205А;

I₅=I₅^//−I₅^/=0,2107−0,0501=0,1606 А.

4) Составляем уравнение баланса мощностей цепи. Определяем мощность источников электрической энергии:

Р_ист=E₁I₁+E₂I₂=20×0,3124+30×0,4806=20,666 Вт.

Мощность приемников электрической энергии:

Р_пр=I₁²(R₁+R₀₁)+I₂²(R₂+R₀₂)+I₃²R₃+I₄²R₄+I₅²R₅+I₃²R₆=

=0,3124²(64+1)+0,4806²(43+2)+0,0076²×31+0,32²×25+0,1606²×52+0,0076²×14=20,641 Вт.

Уравнение баланса мощностей:

Р_ист=Р_пр; 20,666≈20,641.

5) Результаты расчетов токов по пунктам 2 и 3 представляем в виде таблицы и сравниваем.

Ток в ветви   Метод расчета	I1, A	I2, A	I3, A	I4, A	I5, A
Метод контурных токов	0,3124	0,4806	0,0076	0,32	0,1606
Метод наложения	0,3129	0,4811	0, 0076	0,3205	0,1606

Результаты расчета токов ветвей обоими методами практически одинаковы.

6) Определяем ток во второй ветви методом эквивалентного генератора.

Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 1.4), т. е. при отключенном потребителе R₂ от зажимов «C» и «D».

 

Лист

 

Обозначим на схеме токи холостого хода ветвей. Для дальнейших расчетов нам необходим только ток I_5х. Вычислим ток методом «свертывания цепи». Определяем эквивалентное сопротивление цепи относительно источника Е_1.

R₃₆=R₃+R₆=45 Ом;

R₄₅=R₄+R₅=25+52=77 Ом;

R_36.45 = 28,4 Ом;

R_э =R_36.45+R_1.01=28,4+65=93,4 Ом.

I_1х= 0,2141 А;

I_5х=I_1х 0,079 А.

Для определения ЭДС эквивалентного генератора находим напряжение холостого хода между зажимами «D» и «C». Составим по второму закону Кирхгофа уравнение для выделенного круговой стрелкой контура:

E₂= U_хх−I_5хR₅, отсюда

U_хх=E_Э= E₂+I_5хR₅=30+0,079∙52=34,1 B.

Лист

Внутреннее сопротивление эквивалентного генератора определяем как входное сопротивление пассивного двухполюсника, схема которого представлена на рис. 1.5.

 

 

Из предыдущих вычислений

R_1.01346=R₃₆∙R₁.₀₁/(R₃₆+R₁.₀₁)+R₄=45∙65/(45+65)+25=51,6 Ом.

R_э= R_1.01346∙R₅/(R_1.01346+R₅)+R₀₂=51,6∙52/(51,6+52)+2=27,9 Ом;

Заменив активный двухполюсник эквивалентным генератором, мы получили схему простейшей электрической цепи с источником Е_Э,R_Э и нагрузкой R₂. Тогда ток во второй ветви будет равен:

I₂= = =0,481 A,

т. е. ток в этой ветви мало отличается от результатов, полученных в пунктах 2 и 3.

7) Для построения потенциальной диаграммы возьмем контур ADFCEA. Зададимся обходом контура против часовой стрелки, точку «A» заземлим, то есть потенциал этой точки равен нулю j₁=0.

Определяем потенциалы точек контура.

j₁=0;

j₄=j₁ −I₄R₄=0−0,32∙25=−8 B;

Лист

j₆=j₄−I₂R₂=−8−0,4806∙43=−28,66 В;

j₃=j₆+E₂−I₂R₀₂=−28,66+30−0,4806∙2 =0,38 В;

j₅=j₃+Е₁−I₁R₀₁=0,38+20−0,3124∙1=20 B;

проверим:

j₁=j₅−I₁R₁=20−0,3124∙64 = 0,0064 B≈0;

Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат – потенциалы точек с учетом их знака. Потенциальная диаграмма построена на рисунке 1.6.

 

Рис. 1.6

Лист

1.2. Расчета нелинейных электрических цепей постоянного тока

Построить входную вольтамперную характеристику схемы (рис). Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики.

Использовать вольтамперные характеристики элементов «а» и «б» (рис.2.1).

 

Дано:

U=110 В,

=32 Ом

Определить:

 

Расчёт цепи производим графическим методом. Для этого в общей системе координат строим вольтамперные характеристики (ВАХ) линейного и нелинейных элементов: (рис.2.2)

ВАХ линейного элемента строим по уравнению . Она представляет собой прямую, проходящую через начало координат. Для определения координаты второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, тогда соответствующие значение тока Соединив полученную точку с началом координат, получи ВАХ линейного элемента.

Лист

Далее строится общая ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически «сворачиваем» цепь. Начинаем с последовательного участка их ВАХ (нелинейного),и 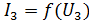(линейного). Так как они соединены последовательно будем для них делать общую ВАХ. Для этого задаемся током и складываем напряжения. Точка пересечения этих значений тока и напряжения дает одну из точек их общей ВАХ. В результате получаем множество точек и по ним строим ВАХ .

Далее мы имеем характеристики нелинейного элемента и нелинейного элемента (нэ23) , которые соединены между собой параллельно. Строим для них общую ВАХ. В данном случае задаемся напряжением и складываем токи. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи .

Дальнейший расчет цепи производим по полученным графикам.

Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжения находим значение напряжения, равно 200 В (точка «А»). Из этой точки восстанавливаем перпендикуляр пересечением с нелинейным элементом , с нелинейным элементом и с общей ВАХ , получим точки «J» и «P» «B». Это связано с тем, что , и соединены параллельно и напряжение у нас в этом случае не изменяется. Из точки «B» опускаем перпендикуляр на ось тока «Q». Отрезок «BQ» дает нам искомое значение общего тока Когда мы из точки «J» опускаем перпендикуляр на ось тока (точка «F») то у нас ток будет равен Опуская перпендикуляр из точки «P» на ось тока то пересекаем в точках «R» и «T» соответственно. Опуская перпендикуляры из этих точек на ось напряжения, получаем напряжения на каждом участке цепи: и 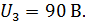Чтобы найти их токи и опускаем перпендикуляр на точку «D», опустив получаем = =2,75 А соответственно. В результате имеем следующие значения токов и напряжений на всех элементах цепи:

 

 

 

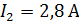
Лист

Лист

Лист

2. Анализ электрического состояния линейных электрических цепей переменного тока: однофазных, трехфазных. Исследование переходных процессов в электрических цепях.

Расчет однофазных линейных цепей переменного тока

Задание

К зажимам электрической цепи подключен источник синусоидального напряжения u=Um*Sin(wt+y_u) B частотой f=50 Гц. Амплитуда, начальная фаза напряжения и параметры элементов цепи:

Um=54 В, y_u= 60°, R₁=10 Ом, R₂=20 Ом, L₁=31,8 мГн, L₂=50,9 мГн, C₁=318 мкФ, C₂=199 мкФ. Схема замещения цепи приведена на рис. 3.1.

 

 

Выполнить следующее:

1) начертить схему замещения электрической цепи, соответствующую варианту, рассчитать реактивные сопротивления элементов цепи;

2) определить действующие значения токов во всех ветвях цепи;

3) записать уравнение мгновенного значения тока источника;

4)

Лист

составить баланс активных и реактивных мощностей;

5) построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений;

Решение

1) Определяем реактивные сопротивления элементов цепи. Угловая частота: w = 2pf = 2∙3,14∙50 = 314 рад/с. Реактивные сопротивления:

X_L1 = wL₁ = 314∙0,0318 = 10 Ом,

X_L2 = wL₂ = 314∙0,0509 = 16 Ом,

X_C1 = 1/wC₁ = 1/(314∙318∙10^-6) = 10 Ом,

X_C2 = 1/wC₂ = 1/(314∙199∙10^-6) = 16 Ом.

2) Комплексная схема замещения цепи представлена на рис. 3.2. Определяем комплексные токи в ветвях и в неразветвленной части цепи. Расчет производим на микрокалькуляторе SR-135, который оперирует комплексными числами в алгебраической форме. Поэтому подставляем числовые значения комплексов в формулы в алгебраической форме.

 

 

Лист

Z ₁ = jX_L1 = j10 = 10 Ом;

Z ₂ = −jX_C2 =−j16 = 16 Ом;

Z ₃ =−jX_C1 = −j10 = 10 Ом;

Z ₄ =(R₁+ R₂)+jX_L2 = (10+20)+j16 =30+j16= 34 Ом.

Выразим действующее значение напряжения в комплексной форме:

U = 38,3 19,2+j33,2 B.

Определяем эквивалентные комплексные сопротивления участков и всей цепи:

Z ₁₂₄=

 

Ом.

Тогда эквивалентное сопротивление цепи

Z _Э= Z ₁₂₃₄= Z ₁₂₄+ Z ₃= =7,86+j5,5=9,59 Ом.

Токи в неразветвленной части цепи:

I = = 3,62 + j1,69 = 4 A;

Напряжение между зажимами сопротивления Z ₁

U ₁= U ₂= U ₄= I · Z ₁₂₄=(3,62 + j1,69)·()=2,26+j69,4=69,4 В.

Остальные токи в ветвях

I ₁= =6,94− j0,226=6,94 A.

I ₃ = =−4,34+j0,141=4,34 A.

I ₄ = 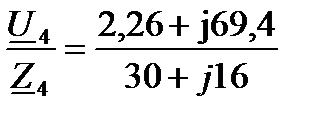=1,02+j1,77=2,04 A.

I ₂ = I ₃+ I ₄=−4,34+j0,141+1,02+j1,77=−3,32+j1,911=3,83 A.

 

3). Уравнение мгновенного значения тока источника:

I = Im∙Sin(wt+y_i)=4∙1,41 Sin(wt +25,03°) = 5,64∙Sin(wt+25,03°) A.

5) Уравнение баланса мощностей в комплексной форме:

S = S ₁+ S ₂+ S ₃+ S ₄; =I² Z ₃+ I ₁² Z ₁+ I ₃² Z ₂+ I ₄² Z ₄;

(19,2+j33,2)∙(3,62 − j1,69)=4²∙(−j10)+ 6,94²∙ j10+4,34²∙(−j16)+

+2,04²∙(30 +j16);

126+j87,7=−j160+j482−j301+125+j66,6 126+j87,7 @ 125+j87,6;

6)

Лист

Напряжения на элементах схемы замещения цепи:

U _R1 = I ₄∙R₁ = (1,02+j1,77)∙10 = 10,2+j17,7 =20,4 B;

U _C1 = – I ∙jX_C1 = –(3,62 + j1,69)∙j10 = 16,9–j36,2 = 40 B

U _C2 = – I ₃∙jX_C2 = –(−4,34+j0,141)∙j16 =2,26+j69,4 =69,5 B

U _R2= I ₄∙R₂ = (1,02+j1,77)∙20 =20,4+j35,4=40,9 B;;

U _L1 = I ₁∙jX_L1 = (6,94− j0,226)∙j10 =2,26+j69,4=69,4 B;

U _L2 = I ₄∙jX_L2 = (1,02+j1,77)∙j16 =−28,3+j16,3=32,7 B;

Для построения векторной диаграммы задаемся масштабами тока М = 1 А/см и напряжения М = 10 В/см. Векторная диаграмма построена на

рис. 3.3

Лист

2.2 Расчет трехфазных линейных электрических цепей переменного тока

Задание

Числовые параметры потребителей заданной трехфазной цепи, соединенных в «треугольник» равны:

Uл=38 B, R_A=1,88 Ом, R_В=3,8 Ом, R_С=3,1 Ом,X_LА=0,68 Ом, X_LC=2,57 Ом, X_CВ=2,2 Ом, схема соединения нагрузки «треугольник»

Определить:

1) фазные токи;

2) линейные токи (при соединении треугольником);

3) активную, реактивную и полную мощность каждой фазы и всей трехфазной цепи;

4) угол сдвига фаз между током и напряжением в каждой фазе;

5) начертить векторную диаграмму трехфазной цепи.

Решение

 

Схема соединения трехфазной нагрузки приведена на рис. 4.1:

 

 

 

Лист

Строгий аналитический расчет трехфазных цепей производится символическим методом, т.е. в комплексной форме.

Определяем систему комплексных фазных напряжений:

U _AВ = U_Ф = 38 В.

U _BС = 380 = – 19 – j32,9 В.

U _CА = 380 = –19 + j32,9 В.

Определяем комплексные сопротивления фаз нагрузки:

Z _АВ = R_А+ jX_LА =1,88+j0,68 =2 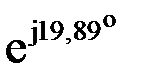Ом;

Z _ВС = R_В–jX_CВ =3,8–j2,2=4,39 Ом;

Z _CА = R_C+jX_LC =3,1+j2,57=4,03 Ом.

Комплексные фазные токи нагрузки:

I _AВ = 17,9–j6,47=19 A;

I _BС = 0,01–j8,65=8,65 A;

I _CА = 1,58+j9,3=9,43 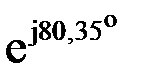A.

Определяем комплексные линейные токи

I _A= I _AB– I _CA =17,9–j6,47–(1,58+j9,3)=16,3–j15,8=22,7 A;

I _B= I _BC– I _AB=0,01–j8,65– (17,9–j6,47) = –17,9– j2,18 =18 А;

I _C= I _CA– I _BC=1,58+j9,3–(0,01–j8,65)=–1,57+j18=18,1 A.

4) Определяем активную, реактивную и полную мощность каждой фазы и всей цепи, используя комплексные мощности:

S _AB=I_AB²∙ Z _АВ=19²∙(1,88+j0,68)=679+j245=722 B∙A;

S _BC=I_BC²∙ Z _ВС=8,65²∙(3,8–j2,2)=284–j165=328 B∙A;

S _CA=I_CA²∙ Z _СА=9,43²∙(3,1+j2,57)=276+j229=358 B∙A.

Определяем мощность трехфазной нагрузки:

Лист

S _AB+ S _BC+ S _CA=679+j245+284–j165+276+j229=1239+j309= =1278 B∙A.

Таким образом:

P_AВ = 679 Вт; Q_AВ = 245 вар; S_AВ =722 ВА; j_АВ=19,89°;

P_ВС = 284 Вт; Q_ВС = –165 вар; S_ВС =328 ВА; j_ВС=–30°;

P_СА = 276 Вт; Q_СА = 229 вар; S_С =358 ВА; j_СА=39,66°.

Для построения векторной диаграммы задаемся масштабами тока тока М=2,5А/см и напряжения М=6,0 В/см. Векторная диаграмма построена на рис. 4.2

 

 

1.4 Исследование переходных процессов в электрических цепях

 

 

Задание

 

При замыкании выключателя цепь (рисунок 5.1), содержащая конденсатор подключается к источнику постоянного напряжения.

 

 

Определить практическую длительность переходного процесса, ток в цепи и энергию электрического поля при t=3t. Построить графики u_C=f(t) и i=f(t).

Числовые параметры схемы:

C=50 мкФ, R=10⁴ Ом, U=50 B.

 

 

Лист

Решение

В данном случае к источнику постоянного напряжения подключаются конденсатор С и резистор R. Напряжение на конденсаторе после замыкания рубильника согласно первому закону коммутации изменяется постепенно от нуля до установившегося значения u_УСТ=U =50 В.

Закон изменения переходного напряжения в цепи с емкостью:

u = u_УСТ+u_СВ = U – U = U(1– 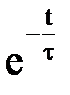) = 150(1– ).

Ток в емкости в переходный период

i = = =0,005 A.

Определяем постоянную времени переходного процесса:

t = RC = 10⁴∙0,00005 = 0,5 с.

Практическая длительность переходного процесса

t = 5t = 5∙0,5 = 2,5 c.

Покажем пример расчета переходных напряжения и тока конденсатора при t=2t:

u = 50∙(1– e^-2t/t) = 50∙(1– e^-2t/t) = 43,2 B.

i = 0,005e^-2t/t = e^-2t/t = 0,000675 A=0,675 мА.

Аналогично рассчитываются значения переходных токов и напряжений для других значений времени и результаты расчета сводятся в таблицу 2.1.

Таблица 2.1

t, c		t	2t	3t	4t	5t
uC, B		31,6	43,2	47,5		49,66
i, мA		1,83	0,675	0,49	0,0916	0,0366

 

Энергия электрического поля конденсатора при t=3t:

W_Э = = 0,056 Дж.

Графики u_C=f(t) и i=f(t)построены на рисунке 8.

 

 

Лист

Литература

1. Ф. Е. Евдокимов. Теоретические основы электротехники.- М. “Высшая школа “,1981 г.

2. В. С. Попов. Теоретическая электротехника. – М. “Энергия”,

1978 г.

3. Ю. В. Буртаев, П. И. Овсянников. Теоретические основы электротехники.– М. “Энергоатомиздат”, 1984 г.

4. Л. А. Частоедов. Электротехника. - М. “Высшая школа”, 1984 г.

5. М. Ю. Зайчик. Сборник задач и упражнений по теоретической электротехнике. – М. “Энергоатомиздат”, 1988 г.

 

 

Лист

Введение

 

Электротехникой в широком смысле слова называется обширная область практиче­ского применения электромагнитных явлений. Широкое и разнообраз­ное использование электрической энергии объясняется тем, что она имеет ог­ромное преимущество перед дру­гими формами энергии. Электрическая энергия сравнительно просто получается из других форм энергии, передается на любые расстояния и легко преобразуется в другие формы энер­гии. Она может сущест­вовать в самых различных количествах и использоваться достаточно экономно. Только на базе электричества оказалось возможным широкое развитие новей­ших научно-технических направлений в радиоэлектронике, в технике связи, в области компью­терных технологий. Трудно представить жизнь современного человека без использования электрической энергии.

Теоретические основы электротехники (ТОЭ) – теоретический курс, в ко­тором в обобщенной форме рассматриваются теория и методы расчета разно­образных электромаг­нитных явлений. Курс ТОЭ занимает основное место среди общетехнических дисциплин, определяющих теоретический уровень профессиональной подготовки инженеров-электри­ков, является теоретической базой для последующего изучения специальных дисциплин. При изложении курса ТОЭ предполагается знание студентами курса физики, в частности, таких ее разделов, как электричество и магнетизм, а также курса высшей математики, в част­ности, таких ее разделов, как теория матриц, дифференциальные уравне­ния и методы их ре­шения (особенно численные), теория функций комплексного переменного, преобразование Фурье-Лапласа, теория поля. При изучении курса ТОЭ предполагается широкое применение современных компьютерных техно­логий.

Электротехники, как научное направление, сформировалось сравни­тельно недавно, хотя первые сведения об электрических и магнитных явлениях дошли до нас из глубокой древности. Слово «электричество» произошло от греческого названия янтаря – электрон. Еще в древности было известно свой­ство натертого янтаря притягивать легкие предметы. Слово «магнит» про­изошло от имени пастуха Магниса, которое упоминается в древне-рим­ской фи­лософии Плиния. Магнис обнаружил, что железный наконечник его посоха прили­пает к неведомым камням.

Однако настоящее рождение электротехники произошло только в ХIХ веке. Ниже приводятся основные (этапные) вехи развития теоретической элек­тротехники.

1747 – 1753 гг. Франклин создает теорию жидкого электричества. Введе­ние в науку понятий батарея, конденсатор, проводник, заряд, разряд, обмотка. Изобретен молниеотвод.

1785 г. Кулон устанавливает взаимодействие электрических зарядов.

Лист

1800 г. Вольт создает первую батарею постоянного тока – вольтов столб.

1820 г. Эрстед устанавливает связь между электрическими и магнитными явлениями. Ампер вводит понятия силы тока и формулирует свои законы.

1831 г. Фарадей открывает явление электромагнитной индукции – одно из величай­ших открытий в области электротехники.

1873 г. Максвелл создает теорию электромагнитного поля – электродина­мику, которая практически в неизменном виде применяется до настоящего вре­мени.

1889 г. Герц открывает явление излучения радиоволн.

1891 г. Доливо-Добровольский создает трехфазную систему переменного тока для энергетики.

1912 г. Штейнметц разрабатывает комплексный метод расчета цепей переменного тока.

1800 – 1880 гг. – период формирования теории цепей постоянного тока.

1880 – 1915 гг. – период формирования теории цепей переменного тока и теории элек­тромагнитного поля.

Курс ТОЭ как самостоятельная учебная дисциплина сформировался в пе­риод 1900 – 1915 гг.

Исторически на территории бывшего СССР сложились две научные электротехни­ческие школы: одна в Москве на базе МЭИ, ее основоположником был К.А. Круг, а вторая – в Ленинграде на базе ЛЭТИ и ЛПИ, ее основополож­ником был В.Ф. Минкевич. Творческое соперничество двух научных школ спо­собствовало успешному развитию теоретических ос­нов электротехники.

 

 

Лист

 

Лист

Содержание

 

Введение………………………………………………………

 

1 Анализ электрического состояния линейных и нелинейных электрических цепей постоянного тока………………………………………………………………....

 

1.1 Расчет линейных электрических цепей постоянного тока………………………………………………………………..

1.2. Расчет нелинейных электрических цепей постоянного тока………………………………………………………………..

 

2. Анализ электрического состояния линейных электрических цепей переменного тока: однофазных и трехфазных. Исследование переходных процессов в электрических цепях………..….………………………………..

2.1 Расчет однофазных линейных цепей переменного тока…………………………….

2.2 Расчет трехфазных линейных электрических цепей

переменного тока……………………………………………

2.3 Исследование переходных процессов в электрических цепях…………………………………………………………………

Заключение…………………………………………………..

Литература……………………………………………………

 

Лист