Основные теоремы о производных

Операция нахождения производной называется дифференцированием; функция, имеющая конечную производную на данном множестве – дифференцируема на данном множестве. Учение о производной и ее приложениях составляет предмет -дифференциальное исчисление.

Рассмотрим основные правила дифференцирования

Производная функции y=f(x) может быть найдена по следующей схеме:

1) аргументу х даем приращение и находим для функции y соответствующее приращение

2) составляем отношение

3) находим предел этого отношения при условии, что . Результат предельного перехода и является производной y’ от функции y по аргументу х, если конечно он существует.

Пользуясь этой схемой, найдем производные от некоторых простейших функций.

1. Производная от степенной функции

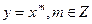
Пусть 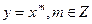. Имеем . Применяя формулу бинома Ньютона, получаем

Тогда и . Следовательно

Имеем теорему

Производная от целой положительной степени независимой переменной равна показателю степени умноженному на основание в степени га единицу меньшую.

1. Производная от функции y=sinx

Пусть y=sinx (x - в радианной мере).

Тогда

. Следовательно y’=(sinx)’=cosx

 

Основные формулы дифференцирования

Предположим, что все рассматриваемые функции определены и дифференцируемы на некотором общем интервале, причем все используемые значения принадлежат данному интервалу.

Производная постоянной величины равна 0.

Пусть f(x)=c, то есть функция одно и тоже значение. При . Тогда

(1)

1. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же алгебраической сумме производных этих функций.

Пусть y=u+v-w, где u,v,w – дифференцируемые функции от х.

Тогда для . Переходя к пределу при и учитывая, что каждое слагаемое имеет предел, находим

. Пользуясь определением производной, окончательно получим y’=u’+v’-w’

Окончательно (u+v-w)’=u’+v’-w’ (2)

Пример

Следствие

Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны между собой.

Действительно [f(x)+c]’=f’(x)+c’=f’(x)=0=f’(x)

1. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй сомножитель плюс произведение первого сомножителя на производную второго сомножителя.

(3)

Пример

Следствие 1

Постоянный множитель можно выносить за знак производной

(cu)’=c’u+cu’=0u+cu’. (cu)’=cu’

Следствие 2

Если y=uvw, где u,v,w – дифференцируемые функции, то

y’=(uvw)’=[(uv)w]’=(uv)’w+(uv)w=u’vw+uv’w+uvw’