Существует внутренний критерий сходимости последовательности исходя из величины элементов. Для формулировки этого критерия введем понятие фундаментальной последовательности.
Определение
Последовательность 
называется фундаментальной, если 
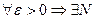, такой, что для всех номеров n, удовлетворяющих условию 
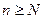и для всех натуральных чисел p (p=1,2,…) справедливо неравенство
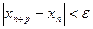
Теорема 1
Для того, чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была ограниченной и чтобы нижний и верхний пределы ее совпадали, то есть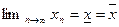 
Теорема 2 (важное свойство фундаментальной последовательности)
Для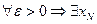 
фундаментальной последовательности, 
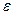- окрестности которого находятся все элементы последовательности, начиная с номера N.
Другими словами, вне интервала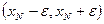 
находится не более чем конечное число элементов последовательности.
Отмеченное свойство позволяет установить ограниченность фундаментальной последовательности.
Пусть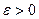 
и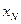 
- элемент, в 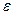- окрестности которого находятся все элементы, начиная с номера N. Тогда вне этой 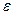- окрестности могут находиться только элементы 
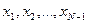. Положим 
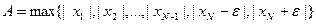. Тогда на сегменте [-A,A] находятся числа 
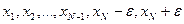, а следовательно, и все точки 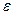- окрестности числа 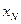. Отсюда вытекает, что все элементы фундаментальной последовательности находятся на сегменте [-A,A], что и означает ее ограниченность.
Теорема. Критерий Коши сходимости последовательности.
Для того, чтобы последовательность была сходящейся необходимо и достаточно, чтобы она была фундаментальной.
Доказательство
Необходимость
Пусть - сходящаяся, и х – ее предел. Требуется доказать, что эта последовательность фундаментальная.
Возьмем 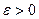. Из определения сходимости последовательности вытекает, что для 
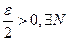, такой, что при 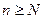выполняется неравенство 
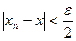. Если 
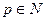, то при 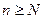выполняется также и неравенство 
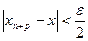. Из последних неравенств получаем
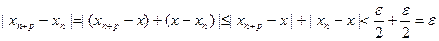. Фундаментальность установлена.
Достаточность
Пусть - фундаментальная последовательность. Требуется доказать, что эта последовательность сходится. Для этого достаточно доказать ограниченность и равенство ее верхнего и нижнего пределов 
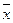и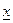 
. Ограниченность фундаментальной последовательности уже была установлена выше. Для доказательства равенства пределов воспользуемся рассмотренным ранее свойством фундаментальной последовательности: Для 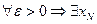фундаментальной последовательности, в 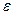- окрестности которого находятся все элементы последовательности, начиная с номера N.
Другими словами, вне интервала 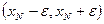находится не более чем конечное число элементов последовательности.
На основании теоремы: (у всякой ограниченной последовательности существует хотя бы одна предельная точка и следствия из данной теоремы) интервал 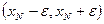содержит интервал 
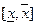, и поэтому 
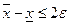, откуда в силу произвольности 
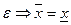. Тем самым сходимость установлена и теорема доказана.
