Интеграл с переменным верхним пределом
Заметим, что в качестве переменной интегрирования можно выбрать любую букву:
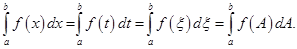
Пусть функция 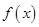 интегрируема на отрезке
интегрируема на отрезке 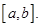 Тогда для любого
Тогда для любого 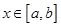 можно вычислить число
можно вычислить число 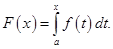 Значит, для каждого
Значит, для каждого 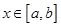 определена функция
определена функция 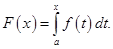 Эту функцию называют интегралом с переменным верхним пределом.
Эту функцию называют интегралом с переменным верхним пределом.
Теорема 1. Если функция 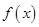 интегрируема на отрезке
интегрируема на отрезке 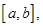 то интеграл
то интеграл  непрерывен на этом отрезке. Если
непрерывен на этом отрезке. Если 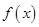 непрерывна на отрезке
непрерывна на отрезке 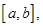 то
то
 дифференцируема на указанном отрезке, причём
дифференцируема на указанном отрезке, причём
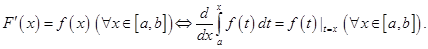

Доказательство первой части этого утверждения опускаем. Перейдём к обоснованию второй части. Пусть 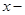 произвольная точка интервала
произвольная точка интервала  Вычислим
Вычислим
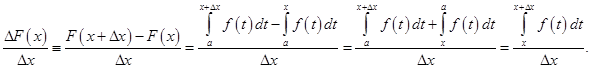
Так как 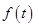 непрерывна на отрезке
непрерывна на отрезке 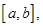 то применима теорема о среднем: существует точка
то применима теорема о среднем: существует точка  такая, что
такая, что

Тогда 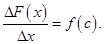 Устремляя здесь
Устремляя здесь 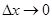 и учитывая, что при этом
и учитывая, что при этом 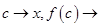
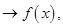
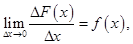 т.е.
т.е.  Равенство (1) показано в любой внутренней точке отрезка
Равенство (1) показано в любой внутренней точке отрезка 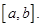 Можно показать, что оно верно и на концах этого отрезка. Теорема доказана.
Можно показать, что оно верно и на концах этого отрезка. Теорема доказана.
Следствие 1. Любая непрерывная на отрезке 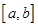 функция
функция 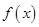 имеет первообразную.
имеет первообразную.
Действительно, в качестве одной из первообразных можно указать интеграл 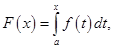 с переменным верхним пределом (
с переменным верхним пределом (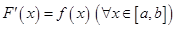 ).
).
Формула Ньютона-Лейбница
Докажем теперь одну из основных формул интегрального исчисления.
Теорема 2. Пусть функция 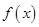 непрерывна на отрезке
непрерывна на отрезке 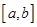 и
и  её первообразная на отрезке
её первообразная на отрезке 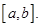 Тогда
Тогда
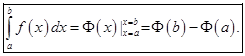

Доказательство. Так как  первообразная функции
первообразная функции 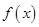 на отрезке
на отрезке 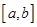 , то существует постоянная
, то существует постоянная  такая, что
такая, что 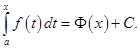 Положим в этом равенстве
Положим в этом равенстве 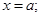 будем иметь
будем иметь  Поэтому
Поэтому
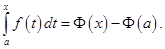
Полагая здесь 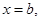 получаем формулу (2). Теорема доказана.
получаем формулу (2). Теорема доказана.
Например, 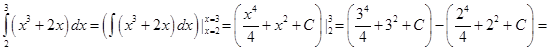
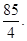
3. Замена переменных и интегрирование по частям в определённом интеграле
С помощью формулы Ньютона-Лейбница нетрудно доказать следующие утверждения.
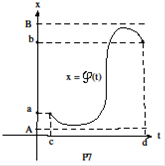
Теорема 3 (см. Р7). Пусть функция 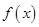 непрерывна на отрезке
непрерывна на отрезке 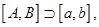 а функция
а функция 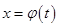 непрерывно-дифференцируема на отрезке
непрерывно-дифференцируема на отрезке 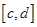 таком, что
таком, что 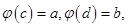 причём
причём 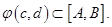 Тогда имеет место формула замены переменных в определённом интеграле:
Тогда имеет место формула замены переменных в определённом интеграле:

Теорема 4. Пусть функции 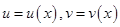 непрерывно-дифференцируемы на отрезке
непрерывно-дифференцируемы на отрезке 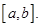 Тогда имеет место формула интегрирования по частям в определённом интеграле:
Тогда имеет место формула интегрирования по частям в определённом интеграле: 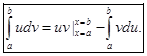
Интегрирование дробно-рациональных функций
Дробно-рациональной функцией (или алгебраической дробью) называется функция, представимая в виде отношения двух многочленов:
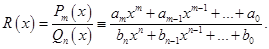
При этом дробь 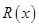 называется правильной, если степень
называется правильной, если степень 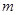 её многочлена-числителя
её многочлена-числителя 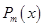 меньше степени
меньше степени  её многочлена-знаменателя
её многочлена-знаменателя 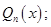 в противном случае (т.е. в случае
в противном случае (т.е. в случае  ) дробь
) дробь 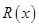 называется неправильной. Любую неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби. Для этого надо разделить числитель на знаменатель углом. Например,
называется неправильной. Любую неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби. Для этого надо разделить числитель на знаменатель углом. Например,
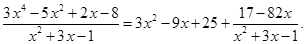
Определение 1. Простейшими дробями типа  называются следующие дроби:
называются следующие дроби:
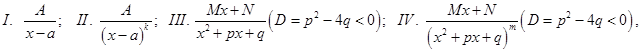 где
где  действительные постоянные,
действительные постоянные, 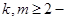 натуральные числа.
натуральные числа.
Теорема 5. Любую правильную дробь 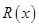 можно разложить в сумму простейших дробей типа
можно разложить в сумму простейших дробей типа  Это разложение единственно (с точностью до порядка слагаемых).
Это разложение единственно (с точностью до порядка слагаемых).




