Пусть функция 
определена на отрезке 
Произведём разбиение (см. Р5)
отрезка 
на частичные отрезки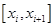 
и выберем произвольно точки 
Вычислим значения
и составим так называемую интегральную сумму
Определение 3. Если существует конечный предел интегральных сумм:
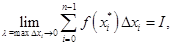
и если этот предел не зависит от вида разбиения и выбора точек 
то его называют определённым интегралом от функции на отрезке Обозначение: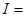 
При этом саму функцию называют интегрируемой на отрезке
(заметим, что число 
называется диаметром разбиения ).
Пусть теперь функция 
По разбиению строится ступенчатая фигура (см. Р6), состоящая из прямоугольников 
высоты 
и длиной основания, равной 
Площадь этой ступенчатой фигуры (достройте её самостоятельно) равна интегральной сумме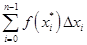 
и эта площадь будет приближённо равна площади криволинейной трапеции[2] 
т.е. 
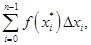причём это равенство будет тем точнее, чем меньше диаметр разбиения 
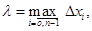и оно становится точным при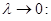 
Мы пришли к следующему геометрическому смыслу определённого интеграла:
интеграл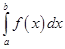 
численно равен площади 
криволинейной трапеции 
с верхней границей, описываемой уравнением 
Замечание 3. В определении 3 интеграла 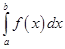предполагается, что отрезок интегрирования ориентирован от 
до 
(т.е. 
). В случае противоположной ориентации отрезка
(т.е. при 
) полагаем по определению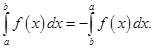 
Также полагаем по определению, что 
Перейдём к формулировке свойств определённого интеграла.
Ограниченность подынтегральной функции. Если функция 
интегрируема на отрезке 
то она ограничена на этом отрезке (т.е. 
).
Линейность интеграла. Если функции и 
интегрируемы на отрезке то на этом отрезке интегрируема и любая их линейная комбинация 
и имеет место равенство 
Аддитивность интеграла. Если функция интегрируема на максимальном из отрезков 
то она интегрируема и на двух других отрезках, причём имеет место равенство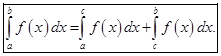 
Далее везде предполагаем, что 
Монотонность интеграла. Если функции 
и 
интегрируемы на отрезке и 
то 
Интегрируемость модуля. Если функции интегрируема на отрезке то на этом отрезке интегрируема и функция 
причём имеет место неравенство
Теорема о среднем для интеграла.Пусть функция непрерывна на отрезке Тогда существует точка такая, что (геометрический смысл этой теоремы состоит в том, что существует прямоугольник с основанием и высоты равновеликий криволинейной трапеции).
Доказательство. Пусть 
(по теореме Вейерштрасса значения 
и 
функцией достигаются). Имеем 
поэтому из свойства монотонности интеграла отсюда получаем
Последние неравенства показывают, что значение 
является промежуточным для функции на отрезке а, значит, по теореме Больцано-Коши существует 
такое, что
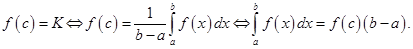
Теорема доказана.
Рассмотрим ещё несколько примеров, которые демонстрируют простейшие приёмы интегрирования.
[1] Здесь и всюду далее с тем, чтобы не прерывать выкладки, в квадратных скобках будем указывать соответствующие замены переменных или формулы, необходимые для преобразований исходных выражений.
[2] На рис. Р6: – это трапеция ограниченная сверху кривой снизу– осью, с боков– прямыми и