Лекция № 1. Матрицы и определители.
План лекции
1. Определение матрицы. Виды матриц.
2. Линейные операции над матрицами.
3. Умножение матриц.
4. Определители второго и третьего порядков. Их свойства.
5. Обратная матрица.
6. Ранг матрицы.
Список литературы
1. Виленкин, И.В. Высшая математика для студентов экономических, естественно-научных специальностей вузов: учеб. пособие / И.В. Виленкин, В.М. Гробер. – Ростов н/Д: Феникс, 2002.
2. Виленкин, И.В. Задачник по математике. Часть 1 / И.В. Виленкин, О.Е. Кудрявцев, М.М. Цвиль, С.И. Шабаршина. – Ростов н/Д: Российская таможенная академия, Ростовский филиал, 2007.
3. Ермаков, В.И. Общий курс высшей математики для экономистов: учебник / Под общ. ред. В.И. Ермакова – М.: ИНФРА – М,2008.
4. Кремер, Н.Ш. Высшая математика для экономистов: учебник / Н.Ш. Кремер, Б.А. Путко, И.М. Фридман. – М.: Банки и биржи, ЮНИТИ, 2002.
Определение матрицы. Виды матриц.
Определение. Матрицей размера  называется прямоугольная таблица чисел, содержащая
называется прямоугольная таблица чисел, содержащая  строк и
строк и  столбцов
столбцов
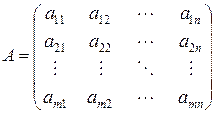 .
.
Каждый элемент матрицы  имеет два индекса:
имеет два индекса:  – номер строки и
– номер строки и  – номер столбца. Например, в матрице
– номер столбца. Например, в матрице

размера  ,
,  ,
,  ,
,  .
.
Часто используется краткая запись матрицы:  .
.
Определение. Матрица называется квадратной  -го порядка, если она состоит из
-го порядка, если она состоит из  строк и
строк и  столбцов. Матрица размера
столбцов. Матрица размера  называется матрицей-строкой, а матрица размера
называется матрицей-строкой, а матрица размера  матрицей-столбцом.
матрицей-столбцом.
Нулевой матрицей 0 заданного размера называется матрица, все элементы которой равны 0.
Единичной называется квадратная матрица, элементы главной диагонали которой равны 1, а все остальные элементы равны 0:
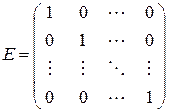 .
.
Можно говорить о единичных матрицах любого порядка.
Определение. Транспонированной для матрицы  называется матрица
называется матрица  , строки которой являются столбцами матрицы
, строки которой являются столбцами матрицы  , а столбцы – строками
, а столбцы – строками  . Например, если
. Например, если
 , то
, то 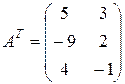 .
.
Матрицы  и
и  называются равными, если
называются равными, если  ,
,  ,
,  .
.
Линейные операции над матрицами.
Определение. Суммой матриц  и
и  называется матрица
называется матрица 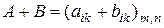 .Складываются матрицы только одинакового размера.
.Складываются матрицы только одинакового размера.
Определение. Произведением матрицы  на число
на число  называется матрица
называется матрица  . Другими словами, для умножения матрицы на число надо каждый элемент матрицы умножить на это число. Любую матрицу можно умножить на любое число.
. Другими словами, для умножения матрицы на число надо каждый элемент матрицы умножить на это число. Любую матрицу можно умножить на любое число.
Для любых матриц одинакового размера и любых чисел  и
и  выполняются свойства:
выполняются свойства:
1) 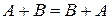 ; ;
| 4)  ; ;
|
2)  ; ;
| 5)  ; ;
|
3)  ; ;
| 6)  . .
|
3. Умножение матриц
Определение. Произведением матрицы 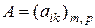 на матрицу
на матрицу  называется матрица
называется матрица  размера
размера  с элементами
с элементами  ,
,  ,
, 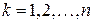 .
.
Другими словами, для получения элемента, стоящего в  -той строке матрицы-произведения на
-той строке матрицы-произведения на  -том месте, следует вычислить сумму произведений элементов
-том месте, следует вычислить сумму произведений элементов  -той строки матрицы
-той строки матрицы 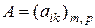 на
на  -тый столбец матрицы
-тый столбец матрицы  .
.
В самом определении произведения матриц заложено, что число столбцов первой матрицы должно совпадать с числом строк второй. Это условие согласования матриц при умножении. Если оно нарушено, то матрицы перемножить нельзя.
Заметим, что вполне возможна ситуация, когда  существует, а
существует, а  нет. Именно так происходит в примере 2. Кроме того, когда существуют оба произведения, то чаще всего они не равны, т.е., вообще говоря,
нет. Именно так происходит в примере 2. Кроме того, когда существуют оба произведения, то чаще всего они не равны, т.е., вообще говоря, 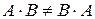 . Приведем еще ряд свойств операции умножения матриц. Если
. Приведем еще ряд свойств операции умножения матриц. Если 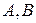 и
и  - квадратные матрицы одного порядка, то справедливы равенства:
- квадратные матрицы одного порядка, то справедливы равенства:
1)  ; ;
| 3) 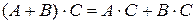 ; ;
|
2)  ; ;
| 4)  . .
|






