Лекция 4
Энергия упругой волны
Процесс распространения волны в каком-нибудь направлении в среде сопровождается переносом энергии колебаний в этом направлении. Допустим, что Δ S – есть часть фронта волны в некоторый момент времени t (рис. 8.1).
>
| х |
| Δ l |
| Δ S |
| Рис. 8.1. Перемещение элемента фронта волны |
По истечении времени Δ t фронт волны переместится на расстояние Δ l = c Δ t, вследствие чего частицы среды в объеме Δ S Δ l приводятся в колебательное движение. Обозначим через w энергию колебаний частиц среды, содержащихся в единице объема (плотность энергии). Допустим, что объем Δ S Δ l очень мал. Тогда в пределах этого объема плотность энергии w всюду одинакова. Можно утверждать, что за время Δ t среда в объеме Δ S Δ l получила энергию w Δ S Δ l. Таким образом, за единицу времени через площадку прошла энергия
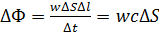(8.1)
Величина ΔФ есть поток энергии волны в единицу времени через площадку Δ S (Δ S ориентируют перпендикулярно направлению распространения волны). Поток энергии – скалярная величина, размерность которой равна размерности энергии [ w Δ S Δ l ], деленной на размерность времени t, т.е. совпадает с размерностью мощности. В соответствии с этим Ф измеряется в ваттах, эргах в секунду и т.п.
Поток энергии в разных точках волны может быть различной интенсивности. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещённую в данной точке, перпендикулярно к направлению, в котором переносится энергия. В соответствии с определением эта величина равна (формула (8.1)):
Так как скорость распространения волны есть вектор, то можно записать
j = w c. (8.3)
Мы получили выражение для вектора плотности потока энергии. Этот вектор был введен в 1874 году русским ученым-физиком Николаем Алексеевичем Умовым и называется вектором Умова. Следует отметить, что вектором Умованазывается вектор плотности потока энергии без конкретизации её физической природы. Выражения для этого вектора были получены Умовым только для упругих сред и вязких жидкостей. В 1884 году идеи Умова были разработаны британским физиком Джоном Генри Пойнтингом применительно к электромагнитной энергии. Потому вектор плотности потока электромагнитной энергии называется вектором Пойнтинга или вектором Умова- Пойнтинга.
Зная величину вектора Умова j во всех точках произвольной поверхности S, можно вычислить поток энергии Ф через всю поверхность. С этой целью разобьем поверхность на элементарные участки dS. За время dt через площадку dS пройдет энергия dW, заключенная в изображенном на рис. 8.2 косом цилиндре. Объем этого цилиндра равен dV = cdtdScosφ, где φ – угол между вектором j и нормалью n к элементарной площадке. В нем содержится энергия dW = wdV = wcdtdScosφ.
| cdt |
| dS |
| φ |
| n |
| j |
| Рис. 8.2. К понятию вектора Умова |
Приняв во внимание, что
wcdScosφ = jdScosφ = ( j, dS ),
где (j,dS) – определение скалярного произведения двух векторов – j и dS = n dS, где n – единичный вектор вдоль нормали к элементарной площадке (известное определение вектора dS элементарной площадки в дифференциальной геометрии). Отсюда для потока d Ф получается формула
Полный поток энергии через поверхность равен сумме элементарных потоков d Ф:
Найдем теперь формулу для расчета плотности энергии w, переносимой плоской волной, например, в твердой упругой среде.
Пусть в такой среде в направлении оси 0 х распространяется плоская продольная волна
Выделим в среде элементарный объем Δ V, настолько малый, чтобы скорость движения частиц и относительную деформацию во всех точках этого объема можно было считать одинаковыми и равными, соответственно, du / dt и du / dx.
Выделенный объем обладает кинетической энергией
где ρ Δ V – масса объема. Если объем дифференциально мал, то
есть плотность кинетической энергии.
Рассматриваемый объем обладает также потенциальной энергией упругой деформации
где х – абсолютное удлинение деформируемого объема, k - коэффициент пропорциональности, фигурирующий в законе Гука F = kx (где F – внешняя деформирующая сила).
Исключим коэффициент k из приведенной выше формулы с помощью закона Гука:
При выводе волнового уравнения для продольных волн в твердой среде мы выделяли элементарный объем в виде цилиндра с поперечным сечением S и высотой Δ х и рассматривали продольное абсолютное смещение u торцов цилиндра. В этих обозначениях энергия упругой деформации запишется в виде
Умножим и разделим правую часть этой формулы на элементарный объем Δ V = S Δ х:
В этой формуле отношение F / S есть так называемое напряжение σ, а из-за малости u и Δ х, отношение u /Δ х – есть относительная деформация среды в точке с координатой х. В пределе при Δ х → 0 величины Δ V и 
можно считать дифференциально малыми и записать
или
Если теперь воспользоваться законом Гука, записанным в виде:
то
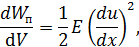
т.е. получаем формулу для энергии упругодеформированной среды, приходящейся на единицу объема, или для плотности потенциальной энергии
Окончательно для плотности механической энергии упругой волны имеем выражение:
Из вывода следует, что эта формула справедлива для любого типа упругих возмущений, распространяющихся в среде, т.е. не только для бегущих волн типа u (t 
но и более сложных зависимостей перемещения u (x, t) от времени и координаты, хотя мы использовали формулу для скорости распространения волн 
В этих случаях под с мы будем понимать формальный параметр, используемый для расчета плотности энергии, а не скорость волны.
Дифференцирование уравнения (8.6) один раз по t, другой раз по х дает для плоской монохроматической волны:
,
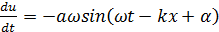Подставив эти выражения в формулу (8.9) и приняв во внимание, что k 2 c 2 = ω2, получим:
Из (8.10) следует, что плотность энергии в каждый момент времени в разных точках среды различна. В одной и той же точке плотность энергии зависит от времени по закону квадрата синуса. Среднее значение квадрата синуса за время, равное периоду Т колебаний, равно ½. Покажем это.
Средним значением некоторой физической величины х за некоторый отрезок времени [ t 0, t 0+ T ] называется интеграл, взятый от этой величины в пределах от t 0 до t 0+ T, деленный на этот отрезок времени.
Среднее значение плотности энергии w, следовательно, выразится как
Учтем, что Т = 2π/ω:
Итак
Плотность энергии (8.10) и ее среднее значение (8.11) пропорциональны плотности среды, квадрату частоты и квадрату амплитуды плоской гармонической волны.
Среднее по времени значение плотности потока энергии называют интенсивностью волны:
Следует заметить, что полученные выражения справедливы и для других упругих волн в жидкостях и газах, а также других видов волн – плоской затухающей, сферической и т.д.
В случае плоской затухающей волны амплитуда уменьшается с расстоянием по закону a = a 0exp(-γ x). Соответственно, средняя плотность потока энергии, т.е. интенсивность волны, убывает по закону
Здесь 
есть начальная интенсивность волны, а k = 2γ – величина, называемая коэффициентом поглощения волны. Для воздуха и некоторых других газов он пропорционален квадрату частоты колебаний: k ≈ 2·10-11ν2 сек2/м; для воды (до ν = 106 Гц) k ≈ 3·10-14ν2 сек2/м, т.е. почти в 700 раз меньше, чем в воздухе. Например, амплитуда колебаний с частотой ν = 106 Гц уменьшается в е = 2,71 раз в воздухе на расстоянии 0,05 м, а в воде – на расстоянии 33,4 м. Этим объясняется широкое применение звуковых и ультразвуковых волн при исследовании морей, при гидролокации и т.д.
В сферической волне, вызванной точечным источником колебаний, плотность потока энергии убывает обратно пропорционально квадрату расстояния от источника. Чтобы показать это, допустим, что источник колебаний ежесекундно отдает в окружающую среду одну и ту же энергию, равную W. Эта энергия равномерно распределяется по шаровой поверхности фронта волны S = 4π R 2, поэтому через единицу площади этой поверхности в единицу времени проходит энергия 
т.е. j ~ 1/ R 2.
Отражение и преломление световых волн.
Принцип Ферма
Известно, что свет распространяется по прямой линии. Посмотрим, что происходит, если свет на своем пути встречает какой-либо объект (рис. 9.1). Простейший объект – это зеркало, и для этого случая известен закон: свет, попадая на зеркало, не проходит через него, а отражается и снова уходит по прямой линии, причем направление прямой меняется при изменении наклона зеркала. Еще в древности людей занимал вопрос: каково соотношение между этими двумя углами? Это очень простое соотношение, и найдено оно было давным-давно. Падающий на зеркало луч после отражения движется по такому пути, что углы между каждым лучом и зеркалом равны. По ряду соображений углы удобно отсчитывать от нормали к поверхности зеркала. Тогда так называемый закон отражения гласит: угол падения равен углу отражения:
θ i = θ r (9.1)
| θ i |
| θ r |
| Рис. 9.1. Угол падения равен углу отражения |
В отличие от простого закона отражения более сложный закон возникает при переходе света из одной среды в другую, например, из воздуха в воду. Хотя в воде свет тоже движется по прямой. Траектория луча в воде образует некоторый угол с траекторией в воздухе. Когда луч падает почти вертикально, угол отклонения θ i невелик. Если же луч направить под большим углом, отклонение становится значительным (рис. 9.2). Возникает вопрос: каково соотношение между двумя углами? В древности эта проблема долго ставила людей в тупик, но ответ тогда так и не был найден. Тем не менее, именно по этому вопросу можно найти очень редкую в древнегреческой физике сводку экспериментальных данных!
| θ i |
| θ r |
| Рис. 9.2. При переходе из одной среды в другую луч света преломляется |
Клавдий Птолемей составил таблицу углов отклонения света в воде для целого ряда углов падения из воздуха. В табл. 9.1 приведены углы в воздухе в градусах и соответствующие им углы для воды. Принято считать, что древние греки никогда не ставили опытов. Однако, не зная закона, такую таблицу можно составить только на основании эксперимента, а не в результате независимых измерений. Так что опыты все-таки ставились.
Таблица 9.1
