Лекция 3
При изучении волновых процессов в самом общем виде ставится следующая задача. Задано колеблющееся тело некоторой формы и размеров. Известны амплитуды, фазы и направления колебаний всех точек этого тела, а также заданы свойства среды. Требуется определить форму и расположение фронта или волновой поверхности в среде в каждый момент времени, а также амплитуды колебаний в различных точках этой поверхности. Для этой цели сначала рассматривается взаимодействие колеблющегося тела со средой и определяется фронт волны в непосредственной близости от этого тела. Дальнейшее распространение волны в среде определяется при помощи принципа Гюйгенса и принципа суперпозиции.
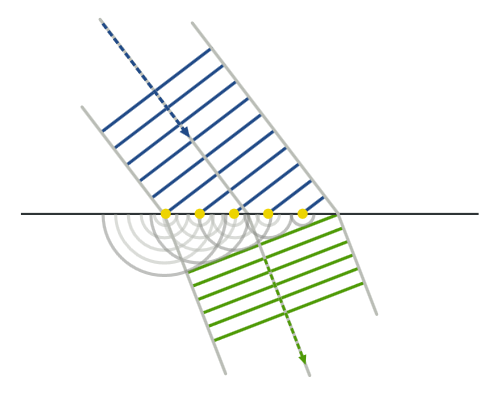
Принцип рефракции или принцип Гюйгенса был введен голландским физиком (а также механиком, математиком, астрономом и изобретателем) Христианом Гюйгенсом в 1678 году. В основе его лежит утверждение, что все точки волнового фронта, заданного в некоторый момент времени t 0, можно рассматривать как самостоятельные источники колебаний, начавшие излучать в момент времени t 0. Эти волны называются элементарными или вторичными. Они могут быть сферическими (если среда изотропная), эллиптическими или иметь иную форму (рис. 5.1).
Принцип Гюйгенса утверждает, что для отыскания фронта волны в последующие моменты времени t = t 0 + Δ t необходимо построить фронты всех элементарных волн через время Δ t и затем провести их огибающую. Эта огибающая есть геометрическое место точек, куда приходит волна в момент времени t. Таким образом, при помощи принципа Гюйгенса можно чисто геометрическими методами определить расположение фронта волны в последующие моменты времени, если это расположение задано в момент времени t 0.
Принцип суперпозиции позволяет определить интенсивность колебательного движения (амплитуду колебаний) в различных точках нового фронта волны, если эта интенсивность была известна во всех точках фронта волны, заданного в момент времени t 0.
Содержание этого принципа заключается в следующем. Предположим, что S есть фронт волны (или волновая поверхность) в момент времени t 0, а S` - в момент времени t = t 0 + Δ t (рис. 5.2). Каждую точку М поверхности S заменяем точечным источником элементарной волны. Эти волны будут сферическими, если среда однородная и изотропная.
|
| Рис. 5.1. Рефракция волн по Гюйгенсу: синие линии и синяя стрелка - фронты падающей волны и направление вектора фазовой скорости в первой среде; желтые точки и серые окружности - вторичные источники на границе раздела двух сред и фронты порожденных ими сферических волн во второй среде; зеленые линии и зеленая стрелка - фронты преломленной волны и направление вектора фазовой скорости во второй среде |
| S ` |
| S ` |
| S |
| S |
| M 1 |
| M 2 |
| M 3 |
| r 1 |
| r 2 |
| r 3 |
| A |
| Рис. 5.2. Принцип суперпозиции |
Фазы колебаний в точках М 1, М 2,… одинаковые, хотя амплитуды могут быть различными. Обычно для простоты рассматривают поверхность S, все точки которой колеблются с одинаковыми амплитудами. В момент времени t элементарные волны от точек М 1, М 2,… дойдут до точки А, лежащей на поверхности S`, причем фазы и амплитуды колебаний, вызванных этими элементарными волнами в точке А, зависят от расстояний r 1, r 2, … согласно формуле сферической волны
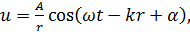(2.11, лекция 1). Принцип суперпозиции утверждает, что амплитуду колебаний в точке А можно найти, сложив все колебания, вызванные в этой точке элементарными волнами, исходящими от поверхности S. При этом обычно предполагается, что все колебания в среде – линейные, поэтому суммарное отклонение u от состояния равновесия равно сумме отклонений u 1+ u 2+…, вызванных каждой элементарной волной в отдельности.
Сложение колебаний в различных точках среды, вызванных несколькими волнами, называется интерференцией этих волн. Суммарное колебание в каждой точке среды зависит от частоты, амплитуды, фазы и направления колебаний, вызванных каждой волной. В частности, если волны имеют одинаковые частоты и приходят в данную точку среды с постоянной разностью фаз (не изменяющейся со временем), то такие волны называют когерентными. Колеблющиеся тела, вызывающе появление в среде когерентных волн, называются когерентными источниками. Например, точки М 1, М 2,… поверхности S колеблются с одинаковыми частотами и фазами, а исходящие от них элементарные волны приходят в точку А с разностями фаз, которые зависят только от расстояний r 1, r 2, … и не изменяются со временем, поэтому все точки волновой поверхности являются когерентными источниками, а формируемые ими элементарные волны – когерентными волнами.
С помощью принципа Гюйгенса и принципа суперпозиции можно решить ряд важных задач по распространению волн в неоднородной и не изотропной среде. В частности, рассмотрим распространение волны в среде, в которой имеются тела, не пропускающие этой волны, поглощающие или отражающие ее. Допустим, плоская волна S, имеющая во всех точках одинаковую амплитуду колебаний, встречает непрозрачное для этой волны тело Р, не пропускающее участок волны АВ. Применим принцип Гюйгенса для момента времени, когда волновой фронт находится в положении S` (рис. 5.3). Построив фронты элементарных волн, исходящих из точек волны М 1, М 2,…, N 1, N 2,…и проведя огибающие I, II и т.д. заметим, что волновой фронт заходит в область R, которую называю областью геометрической тени (из геометрических соображений можно было бы предполагать, что волна, отрезаемая телом, не должна заходить в эту область).
Это проникновение волны в область «геометрической тени» называется дифракцией волны.
При помощи принципа Гюйгенса объясняются также законы отражения и преломления волн на границе раздела двух сред.
| R |
| М 3 |
| М 2 |
| М 1 |
| N 1 |
| N 2 |
| N 3 |
| P |
| A 1 |
| B 1 |
| A |
| B |
| I |
| II |
| I |
| II |
| S |
| S` |
| Рис. 5.3. Дифракция |
Стоячие волны
Рассмотрим практически важный случай интерференции двух гармонических плоских волн одинаковой амплитуды и частоты, распространяющихся в противоположных направлениях (так называемые прогрессивная и регрессивная волны, или прямая (u 1) и обратная (u 2) волны):
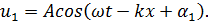
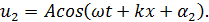(6.1)
Суперпозиция этих волн дает:
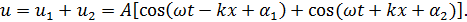
Преобразовав выражение в квадратных скобках по формуле для суммы косинусов (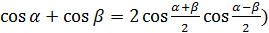
, получаем, что:
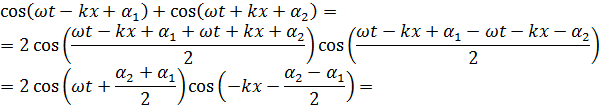
Таким образом
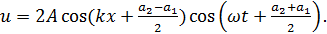(6.2)
Упростим это выражение, для чего произведем сдвиг начал отсчета времени t и координаты x, а именно:
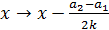и 
Тогда формула (6.2) примет более компактный вид:
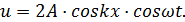(6.3)
или, учтя связь между волновым числом и длиной волны k = 2π/λ, получается
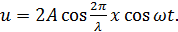(6.4)
Это и есть уравнение стоячей волны (смысл такого названия будет очевиден из дальнейших рассуждений). Из (6.4) видно, что в результате интерференции прямой и обратной волн (6.1) в каждой точке среды (с фиксированной координатой x) происходит гармоническое колебание с той же частотой ω, но с амплитудой
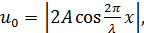(6.5)
в отличие от бегущих волн (6.1) зависящей от значения координаты х.
В точках среды, в которых
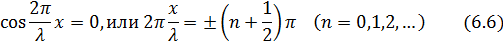
амплитуда колебаний обращается в нуль, т.е. в этих точках колебания отсутствуют вовсе. Эти точки называются узлами стоячей волны. Координаты узлов имеют значения:
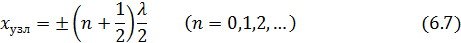
В точках среды, в которых
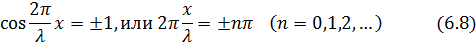
амплитуда колебаний имеет наибольшее значение, равное 2А. Эти точки называются пучностями стоячей волны. Из (6.8) получаются значения координат пучностей:
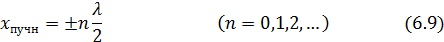
Следует иметь в виду, что пучность, как и узел, представляет собой не одну точку, а плоскость, точки которой имеют значения координаты x, определяемой формулами (6.9) и (6.7).
Легко показать, что расстояние между соседними узлами или соседними пучностями равно λ/2, а пучности и узлы сдвинуты относительно друг друга на четверть длины волны. При изменении х на λ/2 косинус в формуле (2.6) меняет знак на обратный (его аргумент изменяется на π):
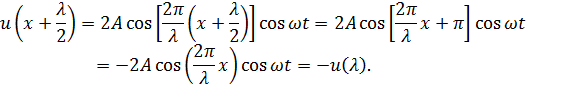
Поэтому, если в пределах одной полуволны – от одного узла до другого – частицы среды отклонились в одну сторону, то в пределах соседней полуволны частицы среды будут отклонены в противоположную сторону. Это означает, что точки, лежащие по разные стороны от узла, колеблются в противофазе. Все точки, заключенные между двумя соседними узлами колеблются синфазно (т.е. в одинаковой фазе). Узлы смещения u как бы разделяют среду на автономные области, в которых гармонические колебания совершаются независимо. Никакой передачи движения из одной области к другой, а значит и перетекания энергии через узлы не происходит. Другими словами, нет никакого распространения возмущения вдоль оси 0 х. Именно поэтому возмущения, описываемые формулой (6.4), и называют стоячей волной. Графически стоячая волна может быть изображена как показано на рис. 5.4. На нем дан ряд «моментальных фотографий» отклонений точек от положения равновесия. Первая «фотография» соответствует моменту времени, когда отклонения достигают наибольшего абсолютного значения. Последующие фотографии сделаны с интервалами в четверть периода. Стрелками показаны скорости частиц.
Характерные особенности стоячей волны в отличие от обычной бегущей волны следующие (имеются в виду плоские волны при отсутствии затухания):
1. В стоячей волне амплитуды колебаний различны в различных местах среды распространения – в системе имеются пучности и узлы; в бегущей волне эти амплитуды везде одинаковы.
2. В пределах участка среды распространения от одного узла до соседнего все точки среды колеблются в одинаковой фазе. При переходе к соседнему такому участку фазы колебаний меняются на обратные. В бегущей волне фазы колебаний зависят от координат точек.
3. В стоячей волне нет одностороннего переноса энергии, как это имеет место в бегущей волне.
| Узел |
| Узел |
| Узел |
| Узел |
| t + T /4 |
| t + T /2 |
| t +3 T /4 |
| t+ T |
| t |
| Рис. 5.4. Стоячая волна ● – отклонения частиц; ● – скорости частиц |
При описании колебательных процессов в упругих системах за колеблющуюся величину можно принять не только смещение u, но и скорость частиц v, величину относительной деформации ε, величину напряжения на сжатие σ, сдвига и т.д.
Продифференцировав уравнение (6.4) один раз по t, а другой раз по х, найдем выражение для скорости частиц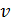 
и для относительной деформации ε:
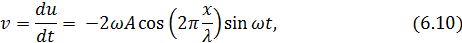
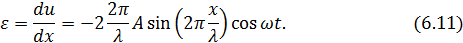
Уравнение (6.10) описывает стоячую волну скорости, а уравнение (6.11) – стоячую волну относительной деформации, причем сдвинуты они относительно друг друга по фазе на π/2 – как в пространстве, так и во времени (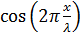
в выражении для 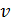меняется на 
в выражении для ε и наоборот, sin ωt заменен на cos ωt). Кроме того, узлы и пучности скорости 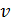частиц среды совпадают с узлами и пучностями их смещения u. Узлы же и пучности деформации ε совпадают, соответственно, с пучностями и узлами смещения u (рис. 5.5).
Соответственно, дважды за период происходят превращения энергии стоячей волны: то полностью в потенциальную (упругую), сосредоточенную, в основном, вблизи узлов (где находятся пучности деформации), то полностью в кинетическую, сосредоточенную, в основном, вблизи пучностей волны (где находятся пучности скорости). В результате происходит перетекание энергии от каждого узла к соседним с ним пучностям и обратно. Средний по времени поток энергии в любом сечении волны равен нулю.
| u |
| u |
| v |
| v |
| ε |
| ε |
| x |
| x |
| x |
| x |
| x |
| x |
| Wp↔Wk |
| Узел v Пучность ε |
| Пучность v Узел ε |
| t=0 |
| t=T/4 |
| Рис. 5.5. Узлы и пучности u, v и ε |
Рассматривая интерференцию прямой и обратной волн, ранее мы не интересовались происхождением этих волн. Допустим теперь, что среда, в которой происходит распространение колебаний, имеет ограниченные размеры. Например, колебания вызываются в каком-нибудь теле ограниченных размеров – в стержне или в струне, в столбе жидкости или газа конечной длины l. В общем случае при возбуждении какого-либо произвольного колебания в таком теле возникает довольно сложное нестационарное движение. Стационарное же движение в виде стоячей волны возможно лишь при вполне определенных частотах. Обратимся, например, к процессу образования стоячих волн в натянутой струне, оба конца которой закреплены. На закрепленных концах струны должны выполняться определенные граничные условия: в них смещение u все время должно равняться нулю. Значит, если в струне возбуждается стоячая волна, то концы струны должны быть ее узлами. Отсюда следует, что на длине струны l должно укладываться целое число n полуволн: l = n λ/2. Из этого условия находим возможные длины волн:
которым соответствуют частоты
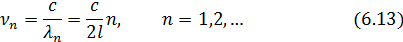
Эти формулы автоматически следуют из уравнения стоячей волны (6.4) при учете граничного условия, а именно, конец l струны закреплен, т.е. смещение u в этой точке равно нулю в любой момент времени:
формальная запись граничного условия, о котором говорилось выше.
При выводе формулы (6.7) для положений узлов начало координат было выбрано так, что первый узел находится на расстоянии четверти длины волны λ/4 вправо от начала координат. Действительно, из (6.7) при n = 0 получается
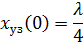
Мы же требуем, чтобы начало оси 0х, связанное со струной, находилось именно в первом узле. Таким образом, эти координаты связаны соотношением:
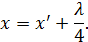
Поэтому условие (6.14) на самом деле выглядит так:
Обратимся к явному выражению для стоячей волны (6.4) и запишем
Поскольку время t может быть произвольным, то нулю равен множитель
откуда
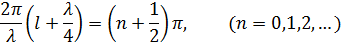
(берем положительные целые числа, так как струна расположена вправо от начала координат).
И мы имеем допустимые длины волн
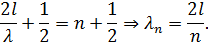
что совпадает с формулой (6.12). Она показывает, что на удвоенной длине струны укладывается целое число собственных длин волн. Наименьшая длина волны равна 2 l (рис. 5.6, на котором изображены собственные колебания).
| l |
| n = 1 |
| n = 2 |
| n = 3 |
| Рис. 5.6. Собственные колебания |
Частоты νn (6.13) называют собственными частотами струны. Частоту ν 1 (n = 1) называют основной частотой, а остальные ν 2, ν 3, … – обертонами. Гармонические колебания с частотами (6.13) называются собственными колебаниями, или гармониками. В общем случае колебания струны представляют собой суперпозицию различных гармоник (спектр).
