Раздел 9.
Общие понятия. Принцип Д¢Аламбера
При статическом действии нагрузок ускорения частиц элементов конструкции при ее деформации невелики и возникающими при этом силами инерции можно пренебречь. Динамической называется такая нагрузка, которая вызывает значительные ускорения частиц конструкции. Эти ускорения могут быть постоянными по величине и направлению, могут быть переменными и знакопеременными. Силы инерции, как и вес – объемные силы, они вызывают добавочные напряжения в конструкции. Влияние ускорений частиц конструкции (и сил инерции) на ее напряженное состояние можно учесть с помощью принципа Д¢Аламбера: «В каждый момент времени любой элемент движущейся конструкции находится в равновесии под действием внешней нагрузки и сил инерции».
При действии динамической нагрузки можно выделить три основные задачи:
I. Учет сил инерции. Здесь ускорения частиц конструкции можно вычислить по правилам кинематики твердого тела и, следовательно, инерционные силы.
II. Удар тел. Здесь ускорения, а значит и силы инерции, зависят от деформации соударяемых тел, которые можно определить методами сопротивления материалов.
III. Колебания тел. Они возникают обычно при действии на конструкцию знакопеременной нагрузки.
Рассмотрим подробнее эти задачи.
I. Учет сил инерции
Величина элементарной силы инерции 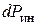 , действующей на частицу тела равна
, действующей на частицу тела равна
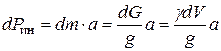 (9.1)
(9.1)
Здесь:  масса, вес, объем частицы;
масса, вес, объем частицы; 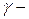 объемный вес материала частицы;
объемный вес материала частицы; 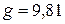 м/сек2 - ускорение свободного падения;
м/сек2 - ускорение свободного падения; 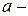 ускорение при движении частицы.
ускорение при движении частицы.
Сила инерции направлена в сторону, противоположную направлению ускорения.
При расчете стержневых конструкций объемные силы инерции удобно представить распределенной погонной инерционной нагрузкой  .
.
Стержень длиной 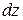 и площадью поперечного сечения А имеет объем
и площадью поперечного сечения А имеет объем  . Подставим это в (9.1)
. Подставим это в (9.1)

Погонная нагрузка – это нагрузка на единицу длины
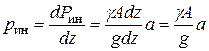 (9.2)
(9.2)
Пример 1. Подъем груза на длинном тросе с постоянным ускорением а.
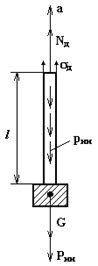
| Дано: 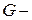 вес груза, вес груза, 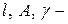 длина, площадь сечения троса и его объемный вес.
В сечении троса на расстояние длина, площадь сечения троса и его объемный вес.
В сечении троса на расстояние 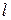 от груза возникает от груза возникает  динамическая сила, которая должна уравновешивать: динамическая сила, которая должна уравновешивать: 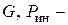 инерционную силу от груза, инерционную силу от груза, 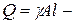 вес троса и вес троса и 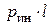 погонную инерционную нагрузку от троса. С учетом (9.1) и (9.2) получим погонную инерционную нагрузку от троса. С учетом (9.1) и (9.2) получим
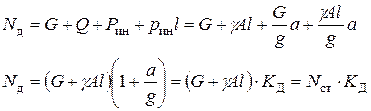 (1) (1)
|
Здесь: 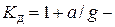 динамический коэффициент,
динамический коэффициент, 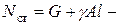 статическое усилие в сечении троса.
статическое усилие в сечении троса.
Обозначим: 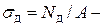 динамическое напряжение,
динамическое напряжение,  статическое напряжение в тросе.
статическое напряжение в тросе.
Поделив (1) на  получим
получим
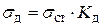
Условие прочности троса  , где
, где 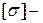 допускаемое напряжение.
допускаемое напряжение.
Пример 2. Вращение стержня в горизонтальной плоскости.

| Дано: 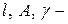 длина, пло-щадь сечения, объемный вес материала стержня; длина, пло-щадь сечения, объемный вес материала стержня; 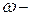 угловая скорость вращения.
На расстояние угловая скорость вращения.
На расстояние 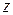 от оси вращения выделим произвольное от оси вращения выделим произвольное
|
сечение. При равномерном вращении стержня центростремительное ускорение 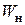 , действующие на частицы стержня в этом сечении, определяется по правилам кинематики
, действующие на частицы стержня в этом сечении, определяется по правилам кинематики 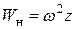 , а погонная инерционная центробежная нагрузка
, а погонная инерционная центробежная нагрузка 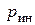 направлена от оси вращения и по (9.2) равна
направлена от оси вращения и по (9.2) равна
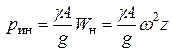 (2)
(2)
Инерционные силы вызывают растяжение стержня силой 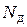 в сечении
в сечении 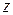 стержня. Т.к
стержня. Т.к 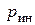 линейно меняется по длине стержня (
линейно меняется по длине стержня (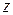 в первой степени в (2)), то
в первой степени в (2)), то 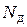 найдем суммированием (интегрированием)
найдем суммированием (интегрированием) 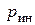 на участке от
на участке от 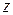 до
до 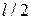
 (3)
(3)
Из (3) видно, 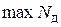 при
при 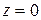 (в середине стержня)
(в середине стержня)
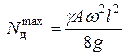 (4)
(4)
Далее можно найти 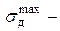 максимальное напряжение в стержне и записать условие его прочности.
максимальное напряжение в стержне и записать условие его прочности.
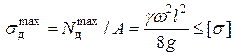 (5)
(5)
Из (5) можно найти max допускаемую скорость вращения  стержня.
стержня.
II. Расчеты на удар тел
Продолжительность удара очень мала и сложно вычислить ускорения частиц ударяемой конструкции. Поэтому, воспользоваться принципом Д¢Аламбера затруднительно и обычно здесь используют закон сохранения энергии.
Для удобства расчета на удар вводят условное понятие динамическая сила  . Эта такая сила, которая, будучи статически приложенной в точке удара, вызовет такие же перемещения (деформации) ударяемого тела, как и при ударе.
. Эта такая сила, которая, будучи статически приложенной в точке удара, вызовет такие же перемещения (деформации) ударяемого тела, как и при ударе.
Расчет на удар без учета массы ударяемого бруса
Рассмотрим закрепленный упругий брус, на который с высоты 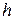 падает груз весом
падает груз весом  . При этом брус может испытывать: а) продольные деформации (колонны, сваи) рис. 9.1а, б) изгибные деформации (балки) рис. 9.1б.
. При этом брус может испытывать: а) продольные деформации (колонны, сваи) рис. 9.1а, б) изгибные деформации (балки) рис. 9.1б.
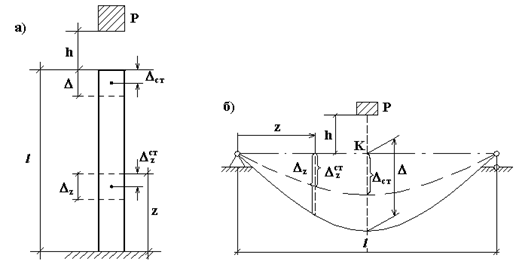
Рис. 9.1
После удара, когда груз  останавливается в нижнем положении, деформации каждого сечения бруса достигают наибольших значений. Их обозначим:
останавливается в нижнем положении, деформации каждого сечения бруса достигают наибольших значений. Их обозначим:  деформации в точке удара,
деформации в точке удара, 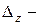 в любом сечении бруса с координатой
в любом сечении бруса с координатой 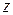 (на рис. 9.1б в эти деформации (прогибы) показаны сплошной линией). Затем происходят затухающие колебания бруса, в конце которых устанавливаются деформации
(на рис. 9.1б в эти деформации (прогибы) показаны сплошной линией). Затем происходят затухающие колебания бруса, в конце которых устанавливаются деформации 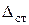 (в точке удара) и
(в точке удара) и 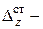 в любом сечении, соответствующие статическому действию груза
в любом сечении, соответствующие статическому действию груза  (на рис. 9.1б эти деформации показаны пунктирной линией).
(на рис. 9.1б эти деформации показаны пунктирной линией).
Расчет проведем при следующих допущениях:
1. Брус идеально упругий, справедлив закон Гука, модуль  одинаков при динамическом и статическом нагружении;
одинаков при динамическом и статическом нагружении;
2. Массу ударяемого бруса пока не учитываем;
3. Эпюра перемещений сечений бруса от удара подобна эпюре перемещений от статического действия груза  . (На рис. 9.1б графики прогибов, обозначенные сплошной и пунктирной линиями, подобны). Обозначим
. (На рис. 9.1б графики прогибов, обозначенные сплошной и пунктирной линиями, подобны). Обозначим
 динамический коэффициент (9.3)
динамический коэффициент (9.3)
Из третьего допущения и рис. 9.1б следует с учетом (9.3)
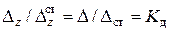 (9.4)
(9.4)
Согласно принятого выше определения динамической силы  , от ее статического приложения возникнут деформации D и
, от ее статического приложения возникнут деформации D и  , а от статического нагружения силой
, а от статического нагружения силой  появятся
появятся 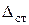 и
и 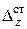 . По закону Гука деформации пропорциональны нагрузкам, поэтому
. По закону Гука деформации пропорциональны нагрузкам, поэтому
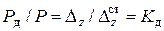 (6)
(6)
По закону Гука и напряжения пропорциональны нагрузкам
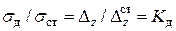 (9.5)
(9.5)
Здесь 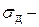 динамические напряжения, т.е. возникают в брусе при ударе;
динамические напряжения, т.е. возникают в брусе при ударе;  статические напряжения, возникают при статическом нагружении силой
статические напряжения, возникают при статическом нагружении силой  .
.
Из (9.4) и (9.5) следует
 (9.6)
(9.6)
Итак, деформации и напряжения в любом сечении бруса при ударе можно определить по (9.6), если вычислить 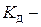 динамический коэффициент. А деформации
динамический коэффициент. А деформации 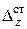 и напряжения
и напряжения  при любом виде статической нагрузки (осевой, изгибной, кручении и т.д.) мы умеем определять из вышеприведенных разделов.
при любом виде статической нагрузки (осевой, изгибной, кручении и т.д.) мы умеем определять из вышеприведенных разделов.
Для решения задачи используем закон сохранения энергии. Груз  при падении проходит путь
при падении проходит путь 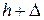 и совершает работу
и совершает работу  .
.
При статическом нагружении силой 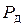 получим ту же деформацию, что и при ударе, потенциальная энергия деформации бруса при этом, как известно, определяется так
получим ту же деформацию, что и при ударе, потенциальная энергия деформации бруса при этом, как известно, определяется так 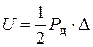 . Сила
. Сила 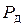 прикладывается в т. К, куда падает груз
прикладывается в т. К, куда падает груз  . По закону сохранения энергии
. По закону сохранения энергии 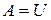 , т.е.
, т.е.
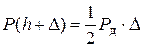 (7)
(7)
Из (6) 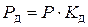 , подставим в (7) получим
, подставим в (7) получим
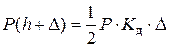 (8)
(8)
Сокращаем на  и учитывая из (9.4), что
и учитывая из (9.4), что 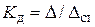 найдем
найдем
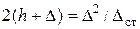 или
или 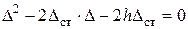 (9)
(9)
Относительно неизвестной 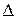 получили стандартное квадратное уравнение типа
получили стандартное квадратное уравнение типа 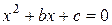
Здесь 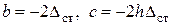 . Решение квадратного уравнения известно из справочников:
. Решение квадратного уравнения известно из справочников:  . В нашем случае получим
. В нашем случае получим
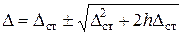 (10)
(10)
При ударе всегда 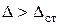 , поэтому выбираем знак (+) и формулу (10) преобразуем так
, поэтому выбираем знак (+) и формулу (10) преобразуем так
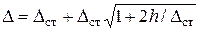 или окончательно
или окончательно 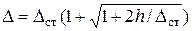 (11)
(11)
Согласно (9.4) 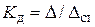 , тогда из (11) получим
, тогда из (11) получим
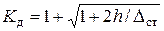 (9.8)
(9.8)
Величина Dст - статическая деформация бруса в точке удара от статического приложения силы  в точке «K» падения груза весом
в точке «K» падения груза весом  . Определяется известными методами:
. Определяется известными методами:
Рис. 9.1а: По закону Гука при осевой нагрузке
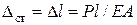
Рис. 9.1б: 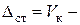 прогиб балки в т. K от силы
прогиб балки в т. K от силы  , приложенной в т. K. Определяется известным методом Клебша из раздела «Плоский изгиб балок».
, приложенной в т. K. Определяется известным методом Клебша из раздела «Плоский изгиб балок».
Скорость груза, падающего с высоты 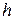 , как известно, определяется так
, как известно, определяется так 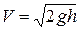 , откуда
, откуда 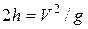 . Подставим это в (9.8) получим
. Подставим это в (9.8) получим
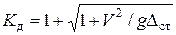 (9.9)
(9.9)
Преобразуем  так:
так:
 (12)
(12)
Здесь: 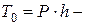 энергия падающего груза в момент начала удара;
энергия падающего груза в момент начала удара;
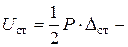 потенциальная энергия деформации бруса от статического нагружения его силой
потенциальная энергия деформации бруса от статического нагружения его силой  в т. K.
в т. K.
С учетом (12) из (9.8) найдем
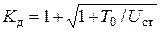 (9.10)
(9.10)
Из (9.8) следует, что чем больше 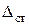 , т.е. чем больше деформируется брус от статической нагрузки
, т.е. чем больше деформируется брус от статической нагрузки  , тем меньше
, тем меньше  и по (9.6) меньше напряжения при ударе. Так появилась идея ставить в конструкциях, испытывающих ударные нагрузки, различные амортизаторы, рессоры, пружины и поясняется поговорка «знал бы, где упаду, подстелил бы солому».
и по (9.6) меньше напряжения при ударе. Так появилась идея ставить в конструкциях, испытывающих ударные нагрузки, различные амортизаторы, рессоры, пружины и поясняется поговорка «знал бы, где упаду, подстелил бы солому».
Пример. Порядок расчета балки на удар.
| На балку с высоты 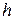 в т. K падает груз в т. K падает груз  . Найти . Найти 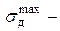 максимальное напряжение в балке от удара, максимальные прогибы в пролете и консоли.
В т. K балки статически при- максимальное напряжение в балке от удара, максимальные прогибы в пролете и консоли.
В т. K балки статически при-
|
кладываем силу  , равную весу груза (рис.б). Определяем от нее опорные реакции и строим эпюру
, равную весу груза (рис.б). Определяем от нее опорные реакции и строим эпюру 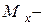 изгибающих моментов. Из Эп.
изгибающих моментов. Из Эп. 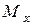 находим
находим 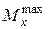 и, зная размеры и форму поперечного сечения балки, вычисляем
и, зная размеры и форму поперечного сечения балки, вычисляем  максимальные напряжения от статического нагружения. Для вычислений по (9.6) надо знать
максимальные напряжения от статического нагружения. Для вычислений по (9.6) надо знать  .
.
Для балки б) со статической силой  для двух участков запишем дифференциальные уравнения изгиба
для двух участков запишем дифференциальные уравнения изгиба 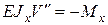 по методу Клебша, интегрируем их и из условий закрепления балки находим константы интегрирования. Строим график прогибов балки, приблизительный вид которого показан на рис.б. Находим
по методу Клебша, интегрируем их и из условий закрепления балки находим константы интегрирования. Строим график прогибов балки, приблизительный вид которого показан на рис.б. Находим 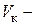 прогиб балки в сечении «K», это и есть
прогиб балки в сечении «K», это и есть  . По (9.8) вычисляем
. По (9.8) вычисляем  и далее
и далее

В консоли максимальный прогиб при ударе 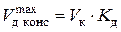 .
.
В пролете находим  максимальный прогиб от статического нагружения и далее максимальный прогиб при ударе
максимальный прогиб от статического нагружения и далее максимальный прогиб при ударе 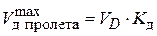 .
.
Дальше можно проверить балку на прочность и жесткость обычными методами.
Существует термин «падение с высоты 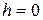 ». Из (9.8) в этом случае получим
». Из (9.8) в этом случае получим 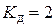 . Чтобы этого не было, груз надо опускать плавно не только до соприкосновения с конструкцией, но и дальше, при перемещении груза вместе с деформируемой конструкцией до полной их остановки.
. Чтобы этого не было, груз надо опускать плавно не только до соприкосновения с конструкцией, но и дальше, при перемещении груза вместе с деформируемой конструкцией до полной их остановки.
Учет массы ударяемого тела (бруса)
Учет массы ударяемого тела достаточно сложен, поэтому приведем окончательные формулы без вывода их.
Динамический коэффициент в этом случае определяется по формулам, аналогичным (9.8)-(9.10)
 (9.11)
(9.11)
Здесь: 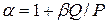 ;
;
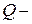 вес ударяемого тела, для бруса
вес ударяемого тела, для бруса 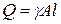
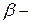 редукционный коэффициент, определяется так
редукционный коэффициент, определяется так
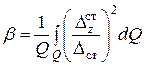 , для бруса
, для бруса 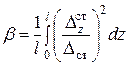 (9.12)
(9.12)
Вычислив 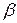 , определяем коэффициент
, определяем коэффициент 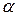 и далее
и далее  .
.
Пример 1. Вычислить 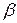 для колонны, показанной на рис. 9.1а. По закону Гука для сечения
для колонны, показанной на рис. 9.1а. По закону Гука для сечения 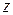 от статического нагружения силой
от статического нагружения силой  :
: 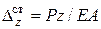 ,
, 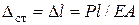 , где
, где  площадь поперечного сечения колонны,
площадь поперечного сечения колонны, 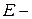 модуль упругости материала.
модуль упругости материала.
 .
.
Пример 2. Вычислить 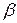 для балки, показанной на рис. 9.1б, когда груз
для балки, показанной на рис. 9.1б, когда груз  падает на середину балки.
падает на середину балки.
Опорные реакции 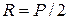 , дифференциальные уравнения изгиба балки от статического нагружения силой
, дифференциальные уравнения изгиба балки от статического нагружения силой  :
:
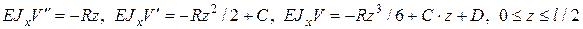 ,
,
т.е. ввиду симметрии ограничимся одним участком.
Граничные условия: 1) 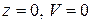 ; 2)
; 2)  (ввиду симметрии), откуда найдем
(ввиду симметрии), откуда найдем 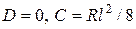 . Тогда
. Тогда  , т.к.
, т.к. 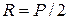 , то
, то 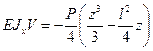 , а
, а 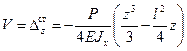 ,
,
подставим  получим
получим 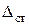 :
:
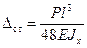 ; Найдем
; Найдем 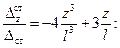
 .
.
Все полученные выше формулы приближенные. Чем большей жесткостью обладает ударяемый брус, тем менее точными будут результаты расчетов. Более точные результаты получаются при рассмотрении волновой теории удара.
III. Колебания тел
Колебания различных конструкций возникают обычно при действии на них знакопеременных нагрузок. Любая упругая конструкция имеет собственную частоту колебаний, определяемую ее жесткостью, массой, размерами, конструктивными особенностями и т.д. Определение собственных частот реальных конструкций – сложная задача. Для приближенных расчетов реальную конструкцию с нагрузкой (балку) заменяют системой грузов, установленных на невесомой балке (рис. 9.2б), т.е. масса балки сосредоточена в грузах. Число грузов определяет, сколько степеней свободы имеет система, заменяющая балку.
 Рис.9.2
Рис.9.2
| Наиболее простое решение можно получить, когда балка заменяется системой с одним грузом (рис. 9.2а). Период свободных колебаний, т.е. время, за которое система совершает одно свободное колебание: |
 [сек]
[сек]
Здесь: 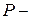 вес груза,
вес груза, 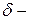 прогиб балки под грузом от силы
прогиб балки под грузом от силы 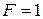 ,
, 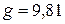 м/сек2.
м/сек2.
Более точно собственную частоту колебаний реальной балки можно установить экспериментально. На балку крепится вибратор, конструкция
 вибратор
вибратор
| которого показана на рис: в корпусе установлены два вала с зубчатыми шестернями (пунктир) и двумя грузами (заштрихованы). Один вал с помощью гибкого шланга вращается электромото-ром постоянного тока (можно плавно изменять |
частоту вращения). Грузы при вращении создают знакопеременные инерционные центробежные силы в вертикальной плоскости, которые действуют на балку. Изменяя частоту вращения валов определяют частоту, при которой резко возрастает амплитуда колебаний балки с вибратором. Это и будет собственная частота колебаний балки, т.к. масса вибратора много меньше массы балки. Здесь учитываются все особенности реальной конструкции балки.
Этот способ основан на явлении резонанса при колебаниях. Резонанс возникает, когда частота внешних силовых импульсов приближается к частоте собственных колебаний конструкции. Явление резонанса играет большую роль в технике. При резонансе резко возрастает амплитуда колебаний конструкции (т.е. деформации и напряжения в ней), что часто приводит к разрушению конструкций. Примерами резонансных колебаний являются: автоколебания подвесных мостов, флаттер частей самолетов (крыльев, хвостового оперения), колебания высотных зданий и сооружений (в них ставят специальные гасители колебаний) и др. В уставе армии есть пункт – в начале движения солдат по любому мосту должна следовать команда «сбить шаг». В истории известен случай, когда частота шагов солдат на мосту оказалась близка к собственной частоте колебаний моста, он вошел в резонанс и разрушился.
Внешние знакопеременные нагрузки могут передаваться на конструкции от различных механизмов, станков и т.д., установленных на них. Конструкции, на которых они установлены, должны иметь собственные частоты колебаний далекие от частот внешних воздействий. Резонанс в большинстве конструкций нельзя допускать, это может привести к их разрушению.
Многочисленные опыты показали, что при действии переменных напряжений, возникающих при колебаниях конструкций, разрушение происходит при напряжениях значительно меньших, чем опасные напряжения при однократном статическом нагружении. Причиной разрушения материала при колебаниях является постепенное развитие микротрещин, которые всегда есть в материале. Это явление называется усталостью материала. Способность материала воспринимать многократное действие переменных напряжений называют выносливостью, а проверку прочности элементов конструкций при действии таких напряжений – расчетом на выносливость (или расчетом на усталостную прочность).
Для расчетов на выносливость используют кривые усталости или кривые Вёлера, которые экспериментально получаются для каждого материала. На рис. показана примерная кривая Вёлера.
 |
Кривая Вёлера





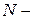 число циклов нагружения до разрушения материала. Видно, что чем меньше
число циклов нагружения до разрушения материала. Видно, что чем меньше  , тем больше циклов выдержит материал. Для
, тем больше циклов выдержит материал. Для
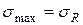 , которую называют пределом выносливости. Это напряжение, при котором не происходит усталостного разрушения данного материала после произвольно большого числа циклов (обычно берут
, которую называют пределом выносливости. Это напряжение, при котором не происходит усталостного разрушения данного материала после произвольно большого числа циклов (обычно берут  циклов).
циклов).
