Раздел 8.
Понятие об устойчивой и неустойчивой формах равновесия.
Понятие о критической нагрузке
Во многих случаях проектирования инженерных сооружений обычных расчетов на прочность бывает не достаточно для того, чтобы сделать вывод о безопасности существования сооружения.
Наряду с проблемой прочности существует проблема устойчивости сооружения или его элементов.
В общем случае при устойчивом равновесии тело, выведенной какой-либо внешней силой из положения равновесия, возвращается в исходное положение после прекращения действия силы.
Случаи устойчивого и неустойчивого равновесия имеются и в статике упругих стержней:
| а) Прямолинейная форма равновесия сжатого упругого стержня при некоторой величине сжимающей силы может оказаться неустойчивой и стержень резко искривится в плоскости наименьшей жесткости. | |
| б) Балка, у которой  , при некоторой величине поперечной силы  оказывается неустойчивой к изгибу и скручивается. Эти явления можно легко обнаружить на опытах с линейкой. Из экспериментов можно выяснить, что устойчивость или неустойчивость формы равновесия упругого тела зависит от его размеров,
| |
формы, материала, условий закрепления, величин и направления сил.
Значение силы (напряжения), при котором первоначальная форма равновесия упругого тела становится неустойчивой, называется критической силой (напряжением) –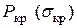 
.
Рассмотрим более подробно работу сжатого стержня. При малой сжимающей силе , меньше критического значения 
, сжатый стержень нечувствителен к малым поперечным возмущениям. При 
прямолинейная форма сжатого стержня становится неустойчивой; достаточно при этом небольшого эксцентриситета приложенной силы, неоднородности материала по сечению или случайного импульса малого поперечного воздействия на него, чтобы стержень искривился. Даже после устранения возмущения стержень останется в изогнутом состоянии. При увеличении 
изгиб будет увеличиваться. Поэтому такое явление называют еще продольным изгибом.
Появление продольного изгиба опасно тем, что при нем происходит очень сильное нарастание прогибов при незначительном увеличении сжимающей силы. Прогибы и нагрузка здесь связаны нелинейной зависимостью. Быстрое нарастание прогибов вызывает рост напряжений от изгиба и часто приводит к разрушению стержня.
Для тонких (гибких) стержней потеря устойчивости наступает при сравнительно небольших сжимающих напряжениях, не являющихся опасными с точки зрения прочности его материала.
История знает немало случаев разрушения инженерных сооружений из-за неправильного расчета их элементов на устойчивость.
Таким образом, продольный изгиб является опасным, его допускать нельзя. Поперечные сечения сжатых стержней должны назначаться не только из условий прочности от сжатия, но из условий того, чтобы сжимающие напряжения были меньше критических напряжений.
Устойчивость сжатых стержней в упругой стадии.
Формула Эйлера.
Задачу определения критической силы (напряжений) впервые решил академик Л. Эйлер в 1744 году.
Заметим, что сама постановка задачи здесь иная, чем во всех ранее рассматриваемых: если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы такое искривление возможно.
Рис.8.1
Для вывода формулы Эйлера рассмотрим шарнирно-опертый, центрально-сжатый стержень постоянного сечения, слегка изогнутый в плоскости наименьшей жесткости. Стержень удерживается в искривленном состоянии силой (см. рис. 8.1). Полагая, что материал стержня работает в пределах закона Гука и деформации стержня малы, для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня, полученным ранее
(а)
Здесь 
прогибы балки, 
. Изгибающий момент в произвольном сечении 
будет равен
(в)
Подставляя (в) в (а) и деля обе части на 
получим
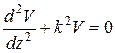, где 
(8.1)
Общий интеграл полученного однородного дифференциального уравнения второго порядка имеет вид:
(8.2)
Это решение включает три неизвестных: А и В – const интегрирования и значение 
, т.к. величина критической силы еще неизвестна. Для определения неизвестных используем следующие граничные условия (см. рис.8.1):
Рис.8.2
1. при 
опора В, поэтому 
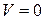и следовательно, из уравнения (8.2) следует
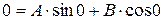, откуда 
Таким образом, изогнутая ось является синусоидой
(8.3)
2. при 
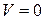, опора С, поэтому . Из уравнения (8.3) получим
Отсюда видно, что или А, или 
равны нулю.
Если 
, то из уравнения (8.3) следует, что прогиб в любом сечении стержня равен нулю, т.е. он не потерял устойчивость, а это не соответствует условию задачи. Следовательно необходимо принять, что 
. Последнее условие выполняется, когда 
принимает значения: 
, где 
любое целое число. Отсюда 
, а т.к. , то 
и отсюда
(8.4)
Из формулы (8.4) следует, что потеря устойчивости стержня возможна при целом ряде значений силы 
. Для практики интересно знать наименьшее значение осевой сжимающей силы, при которой происходит поперечный изгиб. При 
получим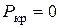 
, что не соответствует условиям задачи. Следовательно, наименьшее значение 
принимает при 
формула Эйлера (8.5)
Для стержня с шарнирными концами значению критической силы по формуле Эйлера соответствует изгиб по синусоиде с одной полуволной [формула (8.3)] и рис.8.2 при
(8.6)
Значениям критической силы высших порядков (при 
) соответствуют искривления стержня по синусоидам с двумя, тремя и т.д. полуволнами. Исследования показали, что формы равновесия при 
и т.д. неустойчивы. Они переходят в устойчивые формы лишь при наличии промежуточных опор в т. В и С (рис. 8.2).
Константа А осталась неопределенной. Физический смысл ее выясняется, если в уравнение синусоиды (8.6) положить 
. Тогда 
. Следовательно, 
это прогиб стержня в середине. Так как при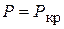 
нами принято, что равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб А остался неопределенным.
