Раздел 5.
Плоский изгиб
Призматический стержень испытывает деформацию изгиба в том случае, если в плоскостях, проходящих через ось стержня, к нему приложены пары сил (моменты) или силы, перпендикулярные к его оси.
Стержень, работающий на изгиб, обычно называется балкой. На балку могут действовать кроме внешних сил и реакции опор. Для решения задач сопротивления материалов обычно необходимо знать и те и другие.
Опыт показывает, что при действии указанных сил ось балки искривляется, т.е. балка изгибается.
В случае, когда изгибающий момент в поперечном сечении балки является единственным силовым фактором, а все остальные равны нулю, имеем чистый изгиб (рис. 5.1а).
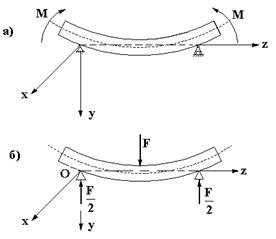 Рис.5.1
Рис.5.1
| Если наряду с изгибающим моментом в поперечных сечениях возникают также и поперечные силы, а нормальная сила (продольная) при этом равна нулю, то имеем поперечный изгиб (рис. 5.1б). Если все силы, в том числе и опорные реакции, лежат в плоскости, совпадающей с осью симметрии сечения, то изогнутая ось балки будет также лежать в этой |
плоскости. Такой изгиб называют плоским изгибом. Мы рассмотрим плоский изгиб в плоскости 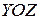 (см. рис. 5.1). Ось
(см. рис. 5.1). Ось 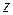 будем направлять горизонтально, слева направо. Ось
будем направлять горизонтально, слева направо. Ось 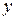 направим вниз, ось
направим вниз, ось  направлена на «нас», при этом оси
направлена на «нас», при этом оси 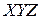 составят правую систему координат.
составят правую систему координат.
Основные типы балок и опорных связей.
Определение опорных реакций
Для того, чтобы балка смогла воспринимать нагрузку и передавать ее на конструкцию, она должна быть соединена с ней опорными связями. Опорные реакции зависят от устройства опорных связей или, как говорят, типа опор. Различают три основных типа опор:
 |
1. Шарнирно-неподвижная опора.
Эта опора допускает свободный поворот сечения балки в плоскости изгиба, но препятствует перемещениям как по вертикали, так и по горизонтали. В такой опоре возникает две составляющие опорной реакции: R - вертикальная и H - горизонтальная.
2.  Шарнирно-подвижная опора.
Шарнирно-подвижная опора.
Эта опора кроме поворота сечения допускает перемещение в одном направлении (в данном случае – по горизонтали). Реакция такой опоры R направлена вдоль опорной связи или перпендикулярна плоскости опирания катков.
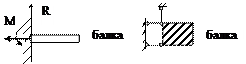 |
3. Заделка
|
Такая опора не допускает ни поворота, ни перемещений по двум направлениям сечения балки, примыкающего к заделке. В заделке возникают реакции R, H и момент М.
Применяют различные варианты прикрепления балки к основанию с помощью рассмотренных опор. Наименьшее число связей, обеспечивающее неподвижность балки по отношению к основанию в одной плоскости, равно трем (рис. 5.2).










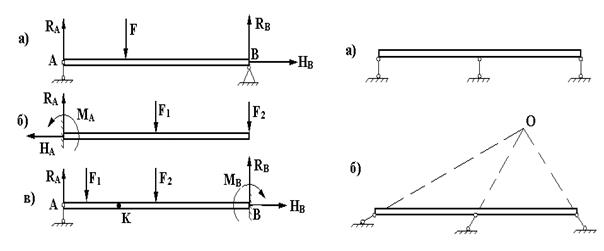
Рис.5.2 Рис.5.3
На рис. 5.2 показаны некоторые типы балок в зависимости от способов крепления к основанию:
а) простая двухопорная балка;
б) балка, заделанная одним концом.
Могут быть балки с консолями.
Встречаются и более сложные типы балок, состоящие из системы брусьев, соединенных между собой связями (рис. 5.2 в). Точка «К» шарнир.
Недопустимые случаи крепления балки: когда все три опорных стержня параллельны друг другу (рис. 5.3а) или когда направления трех опорных стержней пересекаются в одной точке (рис. 5.3б).
Задача определения опорных реакций подробно изучалась в теоретической механике (раздел статика).
При определении опорных реакций необходимо стремиться так составить уравнения статики, чтобы в каждое из них входило только одно неизвестное. Для этого уравнения моментов составляются относительно оси х, проходящей через опорные точки.
При расчете сложных балок (рис. 5.2в) следует иметь в виду, что уравнения равновесия можно применить как ко всей системе в целом, так и к каждому брусу в отдельности. В таких задачах общее число опорных реакций больше трех, но зато и независимых уравнений статики больше трех. Так для системы на рис. 5.2в, можно составить дополнительное условие – равенство нулю момента относительно шарнира «К».
Устройство опор балок в действительности далеко не всегда соответствует разобранным схемам. Поэтому, приступая к определению опорных реакций балки, необходимо технически грамотно схематизировать опорные части, заменяя действительную конструкцию наиболее приближающейся к ней схемой.
Например, если устройство опор балки допускает хотя бы небольшой поворот или перемещение – этого достаточно, чтобы считать опору шарнирной или подвижной.
Внутренние силовые факторы. Метод сечений
Как уже ранее было показано, внешние нагрузки, действующие на сооружение, вызывают появление в нем внутренних усилий, которые определяются уже известным методом сечений, т.е. чтобы определить внутренние силовые факторы в произвольном поперечном сечении, необходимо мысленно рассечь балку на две части плоскостью и рассмотреть равновесие одной из ее частей.
При действии на брус внешних нагрузок, расположенных в плоскости 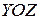 , проходящей через ось бруса и ось симметрии поперечного сечения (т.е в случае плоского изгиба), в каждом поперечном сечении бруса возникают следующие внутренние силовые факторы (ВСФ), действующие в этой же плоскости:
, проходящей через ось бруса и ось симметрии поперечного сечения (т.е в случае плоского изгиба), в каждом поперечном сечении бруса возникают следующие внутренние силовые факторы (ВСФ), действующие в этой же плоскости:
а) продольная сила  , приложенная в центре тяжести сечения
, приложенная в центре тяжести сечения
б) поперечная сила  , проходящая через его центр тяжести
, проходящая через его центр тяжести
в) изгибающий момент 
Из рис. 5.1 видно, что деформация изгиба сопровождается растяжением одних волокон и сжатием других, т.е. в поперечных сечениях возникают нормальные напряжения при изгибе 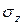 , а внешние поперечные силы уравновешиваются касательными напряжениями
, а внешние поперечные силы уравновешиваются касательными напряжениями 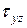 в сечениях.
в сечениях.
В общем случае ВСФ 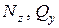 и
и  являются статическим эквивалентом распределенных внутренних напряжений
являются статическим эквивалентом распределенных внутренних напряжений 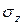 и
и 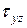 и связаны между собой известными зависимостями (1.6)
и связаны между собой известными зависимостями (1.6)
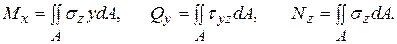 (5.1)
(5.1)
В сопротивлении материалов принято следующее правило знаков для внутренних усилий:
1. Изгибающий момент считают положительным, если он вызывает растяжение нижних волокон.
2. Поперечную силу считают положительной, если она стремиться повернуть вырезанный из балки элемент бесконечно малой длины по ходу часовой стрелки.
Это правило иллюстрируется на рис. 5.4, где показаны положительные направления внутренних силовых факторов как для левой, так и для правой отсеченных частей.
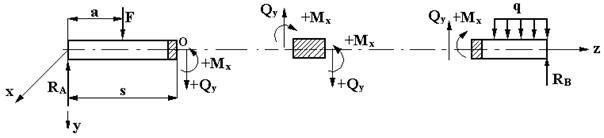
Рис.5.4
Необходимо обратить особое внимание на правило знаков для поперченной силы: для левой отсеченной части 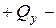 вниз, для правой части
вниз, для правой части 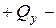 вверх.
вверх.
Внутренние силовые факторы в поперечном сечении определяются из условия равновесия отсеченной части стержня.
Для определения внутренних усилий, действующих со стороны правой части бруса на левую, рассмотрим равновесие левой отсеченной части бруса (рис. 5.4)
1. Сумма проекций на вертикальную ось у дает: 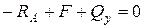 , откуда
, откуда

2. Сумма моментов относительно оси х, проходящей через центр тяжести сечения (т. О) дает:  , откуда
, откуда
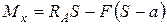
Нетрудно убедиться в том, что внутренние силовые факторы, действующие со стороны правой части на левую равны по величине и противоположны по направлению силовым факторам, действующим со стороны левой части на правую.
Последние определяются из условия равновесия правой отсеченной части.
Из этих соображений можно получить следующее правило для определения внутренних силовых факторов в любом поперечном сечении балки, изложенное в разделе 1 формулы (1.5).
1. Изгибающий момент  относительно центральной оси х в поперечном сечении по величине и по знаку равен сумме моментов относительно этой оси всех внешних сил, приложенных к правой части балки или сумме моментов (относительно той же оси), взятой с обратным знаком, всех внешних сил, приложенных к левой части:
относительно центральной оси х в поперечном сечении по величине и по знаку равен сумме моментов относительно этой оси всех внешних сил, приложенных к правой части балки или сумме моментов (относительно той же оси), взятой с обратным знаком, всех внешних сил, приложенных к левой части:
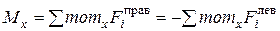 (5.2)
(5.2)
При этом моменты внешних сил 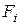 положительны, когда они действуют против хода часовой стрелки и для левой и для правой части.
положительны, когда они действуют против хода часовой стрелки и для левой и для правой части.
2. Поперечная сила  в сечении по величине и по знаку равна сумме проекций на ось у всех внешних сил, приложенных к правой части балки, или сумме проекций (на ту же ось у), взятой с обратным знаком, всех внешних сил, приложенных к левой части бруса:
в сечении по величине и по знаку равна сумме проекций на ось у всех внешних сил, приложенных к правой части балки, или сумме проекций (на ту же ось у), взятой с обратным знаком, всех внешних сил, приложенных к левой части бруса:
 (5.3)
(5.3)
При этом проекции внешних сил на ось у 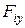 положительны, когда они направлены вдоль оси у, т.е. вниз и для правой и для левой частей балки.
положительны, когда они направлены вдоль оси у, т.е. вниз и для правой и для левой частей балки.
Отметим, что при определении внутренних усилий учитываются внешние моменты и силы, приложенные к балке по одну (и только одну) сторону сечения (т.е слева или справа от сечения).
С невыполнением этого условия связано большинство ошибок при определении внутренних усилий.
Дифференциальные зависимости между Мх, Qy и q
Здесь 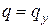 – погонная (распределенная) нагрузка на балку в плоскости
– погонная (распределенная) нагрузка на балку в плоскости 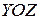 , она принимается положительной, если направлена вниз, т.е. вдоль оси у. В разделе 1 получены более общие дифференциальные уравнения равновесия прямого бруса (1.7), из которых в нашем случае будем использовать следующие (полагая
, она принимается положительной, если направлена вниз, т.е. вдоль оси у. В разделе 1 получены более общие дифференциальные уравнения равновесия прямого бруса (1.7), из которых в нашем случае будем использовать следующие (полагая 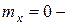 погонный изгибающий момент):
погонный изгибающий момент):
 (5.4)
(5.4)
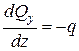 (5.5)
(5.5)
Из двух полученных дифференциальных зависимостей вытекает третья:
 (5.6)
(5.6)
Построение эпюр изгибающих моментов и перерезывающих сил
Для расчетов на прочность необходимо отыскать опасное сечение балки, в котором действуют наибольшие внутренние силы. Для этого необходимо знать закон изменения внутренних усилий в поперечных сечениях балки по ее длине, возникающих от действия на балку нагрузок. Этот закон можно выразить в виде аналитических зависимостей и изобразить с помощью специальных графиков, называемых эпюрами, которые в масштабе изображают значения функций  и
и  на протяжении всей балки.
на протяжении всей балки.
Для определения этих эпюр определяют численные значения моментов и перерезывающих сил для ряда сечений и по ним строят соответствующие эпюры.
На основании зависимостей, характеризуемых выражениями (5.2) и (5.3) легко определить значения  и
и  для любого сечения, а затем построить их эпюры.
для любого сечения, а затем построить их эпюры.
Условимся: на эпюрах  и
и  положительные ординаты откладывать вниз (т.е. вдоль оси у), а отрицательные – вверх от оси балки.
положительные ординаты откладывать вниз (т.е. вдоль оси у), а отрицательные – вверх от оси балки.
Рассмотрим несколько примеров, из которых можно усвоить технику построения эпюр  и
и  .
.
Пример 1.
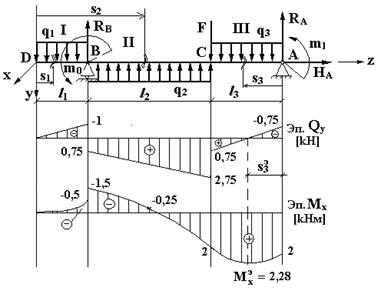 Рис.5.5
Рис.5.5
| Дано: Двухопорная балка с левой консолью. Нагрузки: 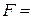 2кН, 2кН, 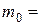 1кНм, 1кНм,  2кНм, 2кНм,  1м, 1м,  2м, 2м, 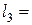 1,5м, 1,5м, 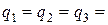 1кН/м (рис.5.5).
Решение задачи:
I. Начнем с определения опорных реакций: опора В – шарнирно-подвижная, в ней может возникнуть 1кН/м (рис.5.5).
Решение задачи:
I. Начнем с определения опорных реакций: опора В – шарнирно-подвижная, в ней может возникнуть
|
только вертикальная реакция  – направим ее произвольно вверх. Опора А – шарнирно-неподвижная, в ней могут быть две реакции:
– направим ее произвольно вверх. Опора А – шарнирно-неподвижная, в ней могут быть две реакции:  горизонтальная и
горизонтальная и  –вертикальная, нарисуем их тоже произвольно. Для определения всех реакций составим три уравнения статики для всей балки:
–вертикальная, нарисуем их тоже произвольно. Для определения всех реакций составим три уравнения статики для всей балки:
1) 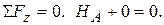 Откуда
Откуда 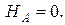
2) Для определения  составим сумму моментов относительно оси х, проходящей через т. А, т.е.
составим сумму моментов относительно оси х, проходящей через т. А, т.е. 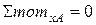 . Все внешние моменты, направленные против хода часовой стрелки, считаем положительными. Все погонные нагрузки
. Все внешние моменты, направленные против хода часовой стрелки, считаем положительными. Все погонные нагрузки 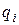 постоянные, поэтому их равнодействующие
постоянные, поэтому их равнодействующие 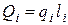 действуют в середине участков.
действуют в середине участков.
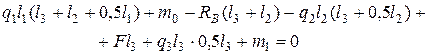
Откуда 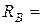 1,75кН.
1,75кН.
Реакция  получилась положительной, следовательно, направив ее вверх, мы угадали ее действительное направление.
получилась положительной, следовательно, направив ее вверх, мы угадали ее действительное направление.
3) Для определения  составим
составим  :
:
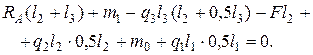
Откуда  = 0,75кН.
= 0,75кН.
Обязательно надо сделать проверку реакций, составив еще одно уравнение статики, например,  , т.е. суммировать все нагрузки и найденные реакции на ось у:
, т.е. суммировать все нагрузки и найденные реакции на ось у:  . Получим 0 = 0.
. Получим 0 = 0.
Итак:  = 0,75кН;
= 0,75кН; 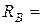 1,75кН;
1,75кН; 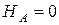 .
.
II. Построение эпюр внутренних силовых факторов. В соответствии с характером конструкции балки и нагрузки делим балку на три участка. Эпюры  и
и  будем строить по участкам, используя метод сечений и формулы (5.2) и (5.3):
будем строить по участкам, используя метод сечений и формулы (5.2) и (5.3):
I участок длиной 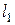 . Проведем сечение в пределах участка. Видно, что проще рассмотреть левую отсеченную часть. Тогда сечение определим расстоянием
. Проведем сечение в пределах участка. Видно, что проще рассмотреть левую отсеченную часть. Тогда сечение определим расстоянием 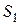 от т. D.
от т. D.  (лев) – пределы изменения
(лев) – пределы изменения 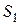 .
.
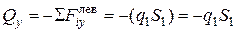
т.е. эпюра  линейна, поэтому для ее построения достаточно двух точек.
линейна, поэтому для ее построения достаточно двух точек.

т.е. эпюра  меняется по закону квадратной параболы, поэтому необходимо не менее трех точек на ней.
меняется по закону квадратной параболы, поэтому необходимо не менее трех точек на ней.
Посчитаем величины  и
и  при следующих значениях
при следующих значениях 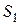 :
:
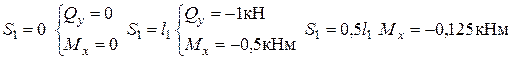
Строим эпюры  и
и  на этом участке, откладывая в масштабе отрицательные значения
на этом участке, откладывая в масштабе отрицательные значения  и
и  вверх от оси бруса.
вверх от оси бруса.
II участок длиной 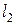 . Рассмотрим тоже левую часть
. Рассмотрим тоже левую часть  (лев)
(лев)
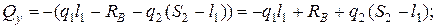

Считаем:
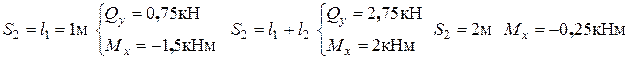 Строим эпюры
Строим эпюры  и
и  на этом участке, учитывая, что для построения
на этом участке, учитывая, что для построения  надо два значения (линейная зависимость), а для построения
надо два значения (линейная зависимость), а для построения  необходимо не менее трех значений
необходимо не менее трех значений  в пределах участка (парабола).
в пределах участка (парабола).
III участок. Проводим сечение, видно, что проще рассмотреть правую отсеченную часть. В этом случае расстояние до сечения  будем отсчитывать от опоры А,
будем отсчитывать от опоры А, 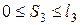 (правая часть)
(правая часть)
а) 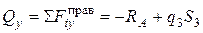
б) 
Считаем:
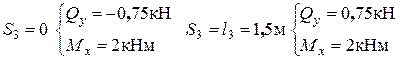
Эпюра  линейна, строим ее по двум точкам. Видно, что при некотором значении
линейна, строим ее по двум точкам. Видно, что при некотором значении 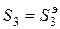 эпюра
эпюра  меняет знак, т.е.
меняет знак, т.е.  = 0, а согласно зависимости (5.4) в этом сечении величина
= 0, а согласно зависимости (5.4) в этом сечении величина 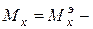 принимает экстремальное значение. Подставим в формулу а)
принимает экстремальное значение. Подставим в формулу а)  = 0 при
= 0 при 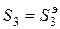 :
:  , отсюда
, отсюда  0,75 м. Подставим
0,75 м. Подставим 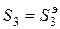 = 0,75 м в формулу б) и найдем
= 0,75 м в формулу б) и найдем 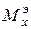 = 2,28 кНм. Это будет третьей точкой для построения эпюры
= 2,28 кНм. Это будет третьей точкой для построения эпюры  .
.
Экстремальные значения 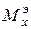 при построении эпюр
при построении эпюр  вычислять обязательно.
вычислять обязательно.
На эпюрах ставим знаки, размерность величин, штриховка перпендикулярна к оси бруса (вертикальная).
Проверка построенных эпюр
Существует несколько способов проверки эпюр, в том числе с использованием зависимостей (5.4) и (5.5). Рассмотрим два самых простых способа:
1. Проверка эпюры  : при движении по эпюре
: при движении по эпюре  (ее обводке) справа – налево скачки на ней должны быть равны по величине и направлению локальным силам, приложенным к балке в этих сечениях. Проверим эпюру
(ее обводке) справа – налево скачки на ней должны быть равны по величине и направлению локальным силам, приложенным к балке в этих сечениях. Проверим эпюру  на рис. 5.5: в сечении А скачок вверх на 0,75кН, здесь действует
на рис. 5.5: в сечении А скачок вверх на 0,75кН, здесь действует 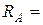 0,75кН вверх; сечение С, здесь скачок вниз от 0,75 до 2,75 т.е. на 2 кН, здесь действует
0,75кН вверх; сечение С, здесь скачок вниз от 0,75 до 2,75 т.е. на 2 кН, здесь действует 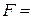 2кН вниз; в сечении В скачок от 0,75 до -1, т.е. на 1,75кН вверх, здесь действует
2кН вниз; в сечении В скачок от 0,75 до -1, т.е. на 1,75кН вверх, здесь действует  = 1,75кН вверх; в сечении D нет скачка и нет силы.
= 1,75кН вверх; в сечении D нет скачка и нет силы.
Итак, во всех сечениях правило выполняется.
2. Проверка эпюры  : скачки на эпюре
: скачки на эпюре  по модулю должны быть равны локальным моментам, действующим на балку в этих сечениях. Проверим эпюру
по модулю должны быть равны локальным моментам, действующим на балку в этих сечениях. Проверим эпюру  на рис. 5.5: в сечении А скачок на 2кНм, здесь действует
на рис. 5.5: в сечении А скачок на 2кНм, здесь действует  2кНм; в сечении В скачок на 1кНм, здесь приложен
2кНм; в сечении В скачок на 1кНм, здесь приложен 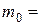 1кНм; больше скачков на эпюре
1кНм; больше скачков на эпюре  нет и на балке нет локальных моментов.
нет и на балке нет локальных моментов.
Итак, во всех сечениях правило выполняется. Наличие на эпюре  скачка без приложенного момента на балке говорит об ошибочности эпюры
скачка без приложенного момента на балке говорит об ошибочности эпюры  .
.
Пример 2.
Криволинейный брус радиуса 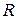 (арка)
(арка)
Дано: 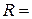 2м,
2м, 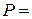 2кН,
2кН, 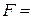 4кН,
4кН, 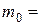 2кНм (рис.5.6)
2кНм (рис.5.6)
|
|
|
|




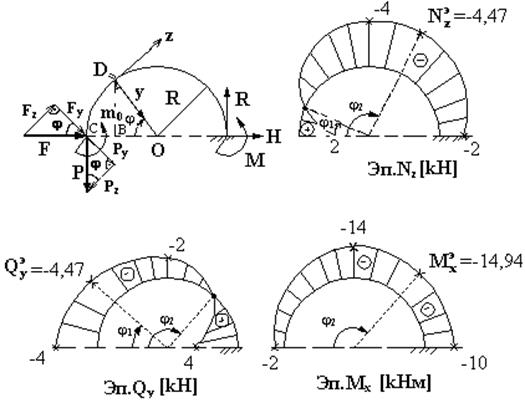
Рис.5.6
Опорные реакции в заделке 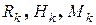 можно определить из обычных трех уравнений статики. По виду конструкции арки и ее нагрузки имеем только один участок. В произвольном месте арки делаем разрез (сечение) в т. D. Очевидно, что проще рассмотреть ту часть арки
можно определить из обычных трех уравнений статики. По виду конструкции арки и ее нагрузки имеем только один участок. В произвольном месте арки делаем разрез (сечение) в т. D. Очевидно, что проще рассмотреть ту часть арки 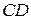 , где приложены нагрузки, тогда не надо определять все реакции опор
, где приложены нагрузки, тогда не надо определять все реакции опор 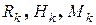 . Положение разреза т. D определим угловой координатой
. Положение разреза т. D определим угловой координатой 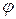 (т. D надо выбрать так на рис. 5.6, чтобы угол
(т. D надо выбрать так на рис. 5.6, чтобы угол 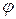 был острым). В сечении D вводим оси
был острым). В сечении D вводим оси 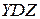 так, чтобы ось
так, чтобы ось 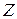 была направлена по касательной к арке в т. D,а ось
была направлена по касательной к арке в т. D,а ось 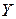 по радиусу. Здесь
по радиусу. Здесь 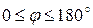 , т.е. в пределах всей арки рассматривается левая часть арки от разреза. Силы
, т.е. в пределах всей арки рассматривается левая часть арки от разреза. Силы 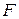 и
и 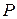 разложим на составляющие по осям
разложим на составляющие по осям 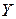 и
и 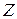 на рис. 5.6. При этом получим два прямоугольных треугольника, в которых необходимо найти
на рис. 5.6. При этом получим два прямоугольных треугольника, в которых необходимо найти 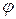 по признакам равенства углов (два угла равны, если их стороны параллельны или взаимно перпендикулярны).
по признакам равенства углов (два угла равны, если их стороны параллельны или взаимно перпендикулярны).
Кроме  и
и  в поперечном сечении арки возникают
в поперечном сечении арки возникают  – внутренние продольные силы, которые определяются по формулам, аналогичным (5.2) и (5.3), полученным в разделе 1.
– внутренние продольные силы, которые определяются по формулам, аналогичным (5.2) и (5.3), полученным в разделе 1.
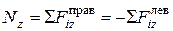 (5.7)
(5.7)
Учитывая, что мы рассматриваем левую отсеченную часть арки, по формулам (5.2), (5.3) и (5.7) получим:
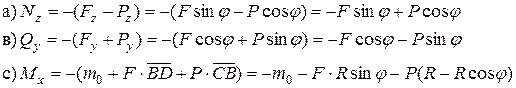 (5.8)
(5.8)
Здесь  и
и  плечи у сил
плечи у сил 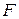 и
и 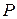 , определяются из рис. 5.6. Все эпюры криволинейны, поэтому определяем не менее трех точек на каждой эпюре по формулам (5.8):
, определяются из рис. 5.6. Все эпюры криволинейны, поэтому определяем не менее трех точек на каждой эпюре по формулам (5.8):
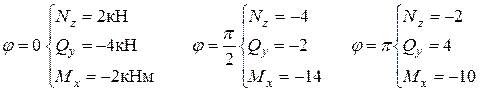
Выбираем масштабы для 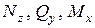 и откладываем полученные значения с учетом знаков: положительные – внутрь, т.е. вдоль оси
и откладываем полученные значения с учетом знаков: положительные – внутрь, т.е. вдоль оси 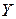 , отрицательные – наружу, против оси
, отрицательные – наружу, против оси 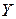 . В каждом сечении величины откладываются по радиусам. На каждой эпюре полученные точки соединяем плавными кривыми. Далее, при необходимости, надо уточнить эпюры с учетом следующих правил:
. В каждом сечении величины откладываются по радиусам. На каждой эпюре полученные точки соединяем плавными кривыми. Далее, при необходимости, надо уточнить эпюры с учетом следующих правил:
1. Если на эпюре  меняется знак, надо найти величину
меняется знак, надо найти величину 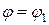 , где
, где  = 0. В этом сечении, при
= 0. В этом сечении, при 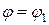 на эпюре
на эпюре  будет экстремум. Для этого в формулу (5.8а) подставим
будет экстремум. Для этого в формулу (5.8а) подставим  = 0 при
= 0 при 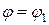 и найдем угол
и найдем угол  . Далее в (5.8в) подставим
. Далее в (5.8в) подставим 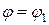 и найдем
и найдем 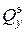 . На нашей эпюре
. На нашей эпюре  этот случай присутствует. Вычислим:
этот случай присутствует. Вычислим:
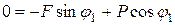
Отсюда  и угол
и угол 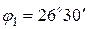
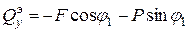 = – 4,47кН
= – 4,47кН
2. Если на эпюре  меняется знак (как у нас), надо найти
меняется знак (как у нас), надо найти  , где
, где  = 0 по (5.8в). В этом сечении, т.е. при
= 0 по (5.8в). В этом сечении, т.е. при  на эпюре
на эпюре  и на эпюре
и на эпюре  будут экстремумы. Вычислим их:
будут экстремумы. Вычислим их:
По (5.8в) 
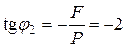 и угол
и угол 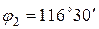
По (5.8а) и (5.8с) найдем при 
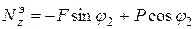 = – 4,47кН
= – 4,47кН
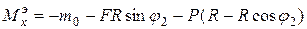 = – 14,94кНм
= – 14,94кНм
Найденные экстремальные значения откладываем на эпюрах и с их учетом строим окончательные эпюры 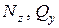 и
и  , которые показаны на рис. 5.6. На эпюрах ставятся знаки, штриховка делается по радиусам.
, которые показаны на рис. 5.6. На эпюрах ставятся знаки, штриховка делается по радиусам.
Нормальные напряжения при чистом изгибе
Выше (см. зависимости (5.1)) было установлено, что при отсутствии в балке продольных сил нормальные напряжения в поперечных сечениях зависят от изгибающего момента, а касательные – лишь от поперечной силы.
Это позволяет упростить вычисление 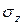 , а именно провести его для случая, когда
, а именно провести его для случая, когда  . Такой случай, как уже было установлено выше, называется чистым изгибом.
. Такой случай, как уже было установлено выше, называется чистым изгибом.
Кроме того полагаем, что балка симметрична относительно плоскости внешних сил, поэтому обе ее половинки деформируются симметрично относительно этой плоскости, т.е. рассматриваем случай плоского изгиба.
Уравнения статики (5.1) в таком случае имеют вид
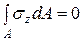 и
и 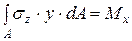 (5.9)
(5.9)
Однако найти 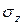 из этих уравнений нельзя, т.к. мы не знаем закона распределения
из этих уравнений нельзя, т.к. мы не знаем закона распределения 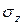 по ординате у.
по ординате у.
Для решения задачи необходимо привлечь условия деформации, которые можно сформулировать только на основании экспериментальных наблюдений. Так, например, если на боковую поверхность бруса нанести сетку в виде продольных и поперечных прямых и загрузить брус по концам положительными изгибающими моментами, то после деформации продольные линии примут криволинейное очертание, а поперечные линии останутся прямыми. Этот факт и другие экспериментальные исследования изгиба балок дают основания для ряда допущений, положенных в основу дальнейших выводов:
1. При чистом изгибе поперечные сечения, плоские до деформации, остаются плоскими и после деформации (гипотеза Бернулли);
2. Продольные волокна друг на друга не давят и испытывают простое линейное растяжение или сжатие;
3. Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков.

 |
Рис.5.7





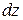 , который после деформации искривляется (рис. 5.7). Два смеж-ных сечения, согласно принятой гипотезе Бернулли, останутся плос-кими, но наклонятся друг к другу, образовав между собой угол
, который после деформации искривляется (рис. 5.7). Два смеж-ных сечения, согласно принятой гипотезе Бернулли, останутся плос-кими, но наклонятся друг к другу, образовав между собой угол 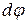 . При этом верхние волокна ока-жутся сжатыми, а нижние рас-тянутыми. На каком-то уровне по высоте балки волокна останутся
. При этом верхние волокна ока-жутся сжатыми, а нижние рас-тянутыми. На каком-то уровне по высоте балки волокна останутся
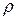 .
.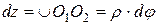 . После деформации его длина стала равной
. После деформации его длина стала равной 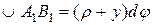 . Абсолютное удлинение
. Абсолютное удлинение 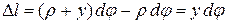 . Относительное удлинение равно
. Относительное удлинение равно
 или
или 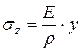 (5.10)
(5.10)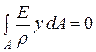
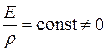 , то
, то
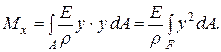
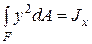

 (5.11)
(5.11) (5.12)
(5.12)
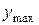 надо подставлять со своими знаками, при этом автоматически получается знак
надо подставлять со своими знаками, при этом автоматически получается знак 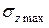 . Это важно для балок, изготовленных из хрупких материалов (чугун, бетон), которые хорошо работают на сжатие и плохо на растяжение. Балки из пластичных материалов (стали) одинаково сопротивляются растяжению и сжатию, поэтому обычно их поперечные сечения симметричны относительно оси х (двутавр), для них
. Это важно для балок, изготовленных из хрупких материалов (чугун, бетон), которые хорошо работают на сжатие и плохо на растяжение. Балки из пластичных материалов (стали) одинаково сопротивляются растяжению и сжатию, поэтому обычно их поперечные сечения симметричны относительно оси х (двутавр), для них и
и 
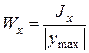 – момент сопротивления симметричного сечения (5.13)
– момент сопротивления симметричного сечения (5.13)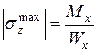 (5.14)
(5.14) »).
»).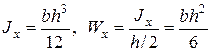

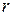

 для стандартных двутавров и швеллеров приводятся в таблицах ГОСТа.
для стандартных двутавров и швеллеров приводятся в таблицах ГОСТа.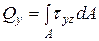
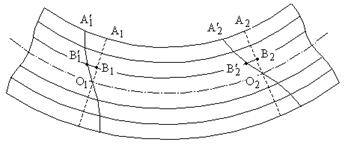 Рис.5.8
Рис.5.8
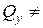 const, т.е.
const, т.е. 
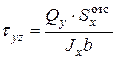 (5.15)
(5.15) ширина сечения, где определяются
ширина сечения, где определяются  статический момент относительно оси х отсеченной части сечения.
статический момент относительно оси х отсеченной части сечения.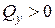 (вниз).
(вниз).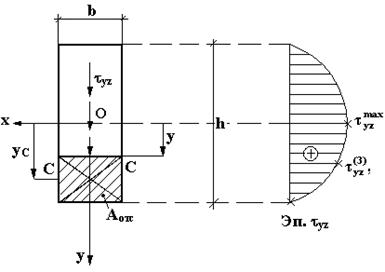
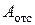 (заштрихована на рис. 5.9). Расстояние от оси х до центра тяжести
(заштрихована на рис. 5.9). Расстояние от оси х до центра тяжести  . Тогда
. Тогда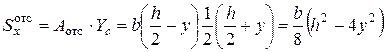
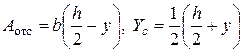
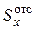 в формулу (5.15)
в формулу (5.15) (А)
(А)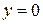 (точка на оси х)
(точка на оси х) 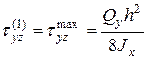
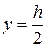
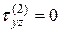




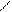


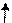





 ), допущения Журавского справедливы и
), допущения Журавского справедливы и  , где
, где 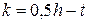 , можно записать с учетом обозначений на рис. 5.10
, можно записать с учетом обозначений на рис. 5.10 (В)
(В)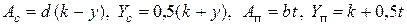
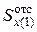 , подставим в (5.15) и вычислим
, подставим в (5.15) и вычислим 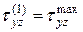 и откладываем ее в масштабе на эпюре
и откладываем ее в масштабе на эпюре 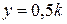 , аналогично вычислим
, аналогично вычислим 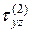 ;
;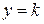 , находим
, находим 
 , которые можно найти по формуле
, которые можно найти по формуле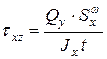 (5.16)
(5.16)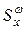 поясним с помощью рис. 5.10.
поясним с помощью рис. 5.10.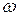 и в этом сечении найдем
и в этом сечении найдем 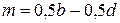 . Тогда
. Тогда 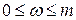 ,
, 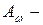 отсеченная площадь
отсеченная площадь (С)
(С)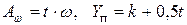
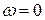 (конец консоли), по (С)
(конец консоли), по (С)  и из (5.16)
и из (5.16) 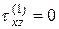 .
.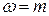 , вычислим
, вычислим 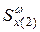 и по (5.16)
и по (5.16) 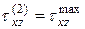
 , направления
, направления  , получим условие прочности
, получим условие прочности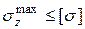
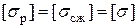 . Поэтому балки из пластичных материалов обычно имеют поперечные сечения, симметричные относительно своих нейтральных осей. Подбор сечения проводится из условия прочности действию наибольшего по абсолютной величине изгибающего момента
. Поэтому балки из пластичных материалов обычно имеют поперечные сечения, симметричные относительно своих нейтральных осей. Подбор сечения проводится из условия прочности действию наибольшего по абсолютной величине изгибающего момента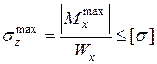 (5.17)
(5.17)

