Пусть 
положительно-определенная матрица, 
начальное приближение к решению системы 
. Следующее приближение 
ищется по формуле
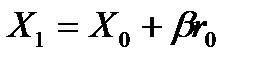
параметр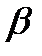 
выбирается так, что бы минимизировалась длина вектора невязки 
. После выполнения первого шага процесс повторяется.
Формулы, связывающие соседние приближения:
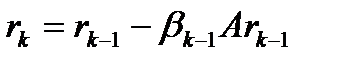
Градиентные методы с неполной релаксацией
Пусть 
положительно-определенная матрица и имеется решение системы .
Рассмотрим итерационный процесс, в котором каждое последующее приближение получается из предыдущего изменением в направлении, противоположному градиенту функции ошибок, причем так, что на каждом шаге функция ошибок уменьшается. Формулы для получения последовательных приближений:
Пусть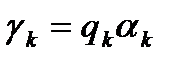 
, где 
соответствующий коэффициент в методе наискорейшего спуска.
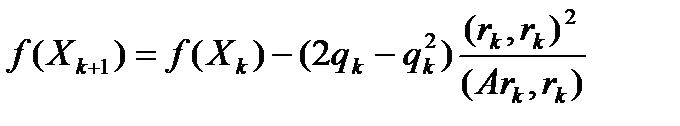
Для того, чтобы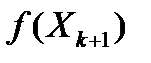 
, было бы меньше, чем 
, необходимо и достаточно выполнение для множителей релаксации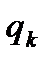 
неравенств
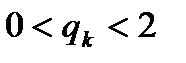
Будем называть группу методов, в которых не все 
равны 1, методами неполной градиентной релаксации. Если все множители релаксация 
, но не все равны единице, метод называется методом нижней релаксации, если все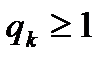 
, но не все 
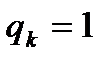,- методом верхней релаксации.
Метод Якоби
Исходную систему АХ=В (1.8.1)
преобразуем к виду:
(1.8.2)
где i=1,2,...,m; aii¹0.
Первая сумма равна нулю, если верхний предел суммирования меньше нижнего.
Так (1.8.2) при i=1 имеет вид
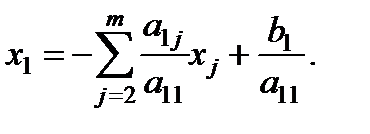
По методу Якоби (метод простых итераций) 
(n+1 приближение хi) ищем по формуле
(1.8.3)
где n – номер итерации (0,1,…,); i=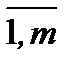 
.
Итерационный процесс (1.8.3) начинается с начальных значений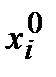 
, которые в общем случае задаются произвольно, но предпочтительнее, если за 
взять свободные члены исходной системы.
Условие окончания счета:
,
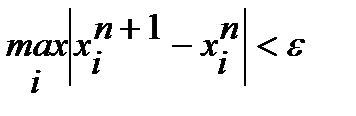где i=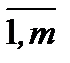 
.
Исходную матрицу системы (1.8.1) представим в виде суммы трёх матриц
A=A1+D+A2,
где D - диагональная матрица;
D =diаg[а11а22…аmm];
A1 - нижняя треугольная матрица;
A2 - верхняя треугольная матрица.
Тогда исходную систему (1.8.1) можно записать в виде
Х=-D-1A1 Х– D-1A2 Х+D-1 В.
Тогда метод Якоби можно записать в виде:
или
. (1.8.4)
Заключение
Список используемой литературы
1. Бахвалов Н.С. Численные методы. – М.: Наука, 1973.
2. Бахвалов Н.С., Жидков Н.П., Кобельников Г.М. Численные методы. – М.: Наука, 2001.
3. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2005.
4. Воеводин В.В. Численные методы алгебры (Теория и алгорифмы). –М.: Наука, 1966.
5. Воеводин В.В., Кузнецов Ю.А, Матрицы и вычисления. – М.: Наука, 1984.
6. Заварыкин В.М., Житомирский Г.В., Лапчик М.П. Численные методы. – М.: Просвещение, 1990.
7. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Численные методы. – М.: Наука, 2007.
8. Калиткин Н.Н. Численные методы. – М.:Наука, 1978.
9. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы (том I). – М.: Наука, 1977.
10. Тарасов В.Н., Бахарева Н.Ф. Численные методы. Алгоритмы. – Оренбург: ИПК ОГУ, 2003.
11. Фадеев Д.К., Фадеева В.Н. Вычислительные методы линейной алгебры. – М.: ФИЗМАТГИЗ, 1963.
