Для того чтобы симметрическая матрица 
была положительно определённой, необходимо и достаточно, чтобы все главные миноры матрицы были положительными:
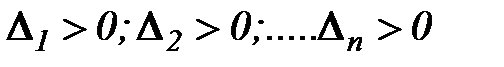
Для отрицательно определенных матриц знаки главных миноров чередуются начиная со знака «-» для: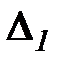 
:
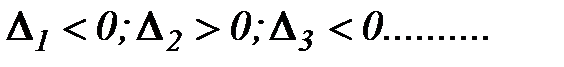
Замечание.
Если матрица знакоопределенная, то все её главные миноры не равны 0.
Экономическая интерпретация
В экономических исследованиях часто приходится сталкиваться с задачей анализа результатов наблюдений
Например, пусть имеются данные о цене нефти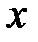 
и индексе нефтяных компаний 
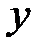, представленные в виде следующей таблицы по результатам биржевых торгов.
| 
| 
| … | 
| … | 
|
| 
| 
| … | 
| … | 
|
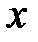
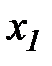
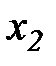
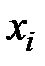
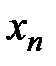
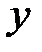
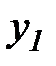
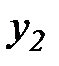
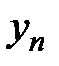
Требуется наилучшим образом сгладить зависимость между переменным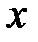и и 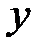, то есть отразить общую тенденцию зависимости 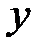от 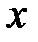в виде эмпирической формулы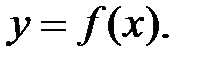 
Для решения подобной задачи используется метод наименьших квадратов.
Задача нахождения эмпирической формулы разбивается на два этапа.
Этап 1. Устанавливается общий вид зависимости 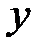от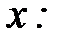 
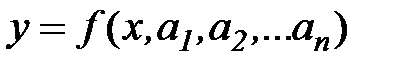
Например, в качестве зависимостей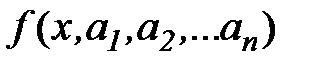 
могут быть взяты:
- линейная функция
;
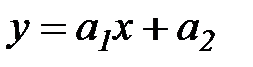-квадратичная функция
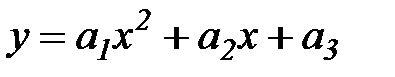
-показательная функция
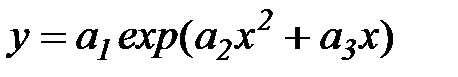
и т.д.
Строится функция
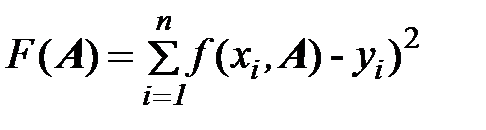(5)
где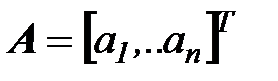 
– вектор неизвестных параметров.
Этап 2.
Решается задача определения неизвестных параметров (6) – задача безусловной оптимизации:
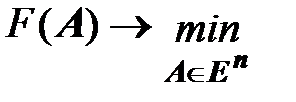(6)
Пусть решением задачи (6) является точка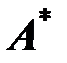 
тогда геометрически это можно представить на рисунке 3.
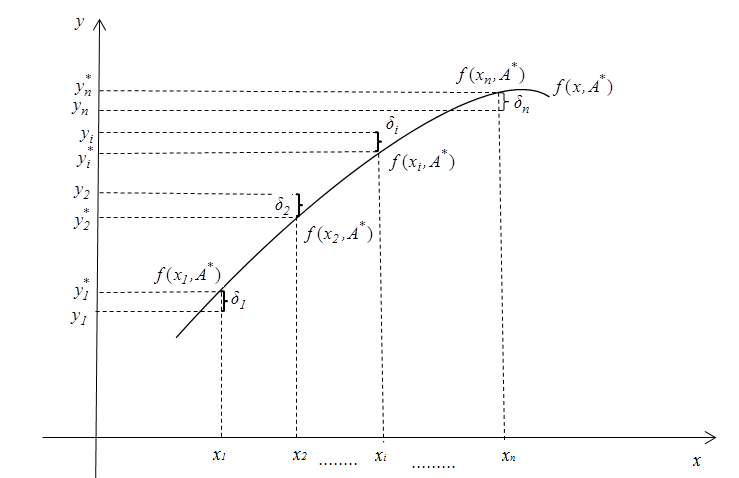
Рис. 3.
То есть кривая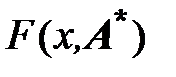 
является наилучшей в смысле минимума суммы квадратов невязок между значениями 
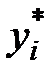, найденными по эмпирической формуле 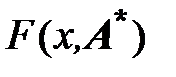и экспериментальными значениями
Рассмотрим конкретную задачу.
Задача 1. Пусть в качестве функции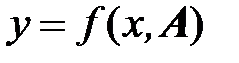 
взята линейная функция: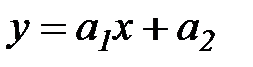
Тогда поиск наилучшей кривой сводится к решению задачи безусловной оптимизации:
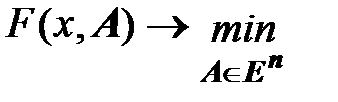(7)
где 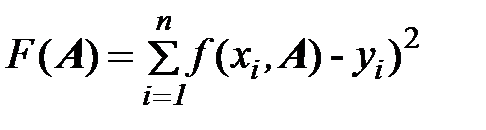зависит от двух переменных 
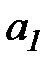и 
.
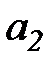Значения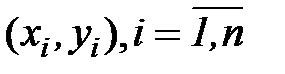 
при решении задачи (7) выступают как постоянные величины.
Вычислим частные производные:
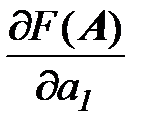и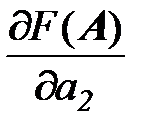 
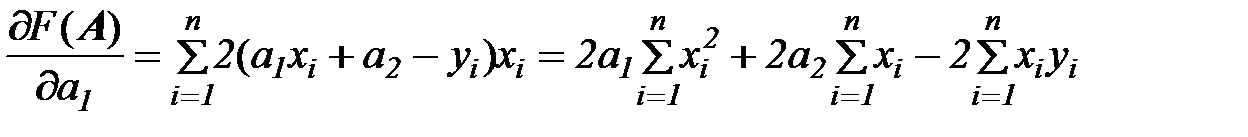
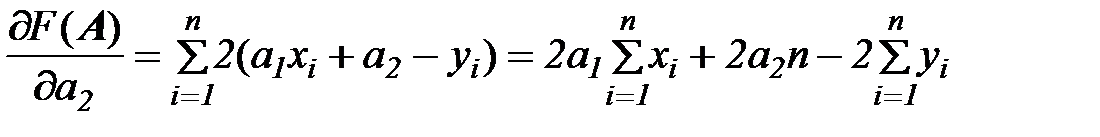
Запишем необходимые условия оптимальности:
; 
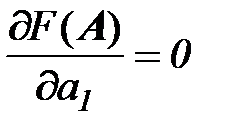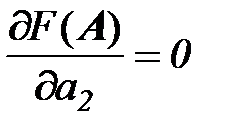
Получим систему двух линейных алгебраических уравнений относительно двух неизвестных 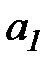и .
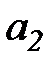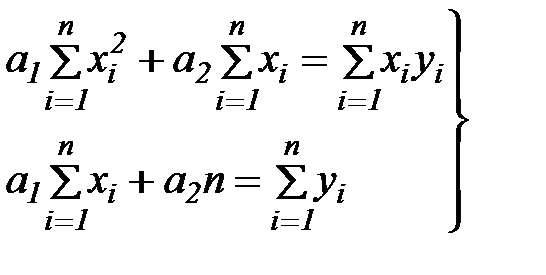(8)
Система уравнений (8) имеет единственное решение (так как определитель системы не равен нулю, а точнее, он больше нуля).
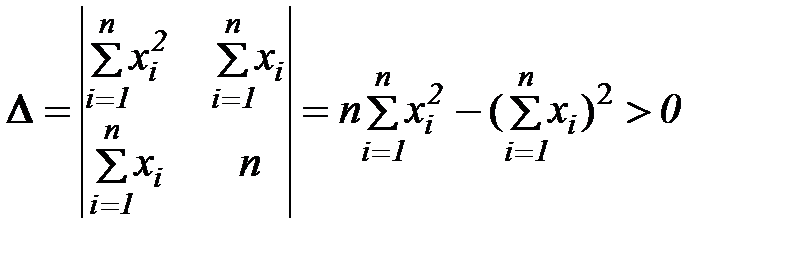
(можно доказать методом математической индукции).
Убедимся что решение системы (8) дает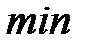 
функции 
.
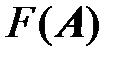Для этого вычислим матрицу Гессиана
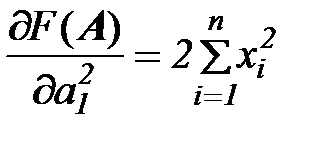
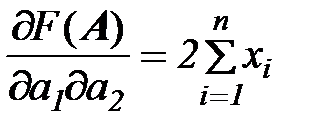
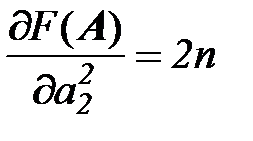
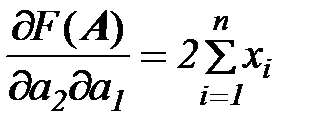
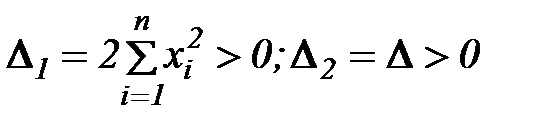(см. выше)
Следовательно, согласно критерию Сильвестра
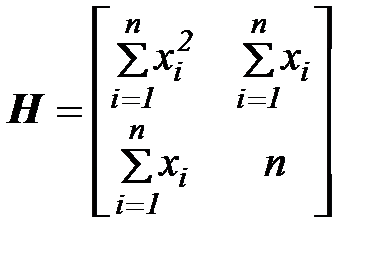
матрица 
является положительно определенной.
Следовательно, стационарная точка 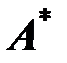являющаяся решением системы уравнений (8), обеспечивает 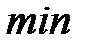функции 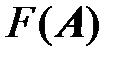в задаче (7).
