Множество действительных чисел и его свойства.
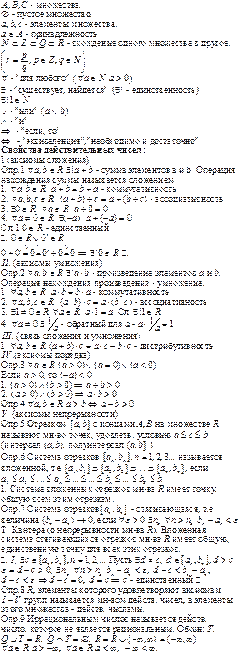
Модуль действ. числа и его свойства.

Функция (отображение). Действительные функции.
Действительные переменные и их простейшие свойства.
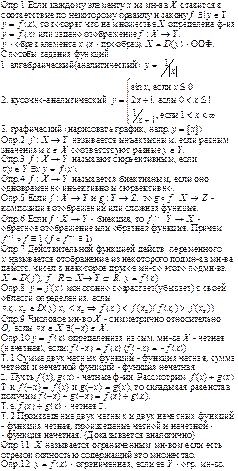
Числовые последовательности. Предел числовой
Числовой последовательности. Число е.

Предел функции в точке. Свойства функций,
Имеющих предел в точке. Предел на бесконечности.
Бесконечные пределы.

Бесконечно малые в точке функции и их свойства.
Необходимые и достаточные условия существования

Арифметические операции над пределами.

Предельный переход в неравенствах.

Односторонние пределы. Необходимое и достаточное
Условия существования предела в точке.

Первый замечательный предел.

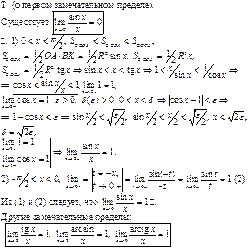
Второй замечательный предел и связанные с ним
Пределы.

Непрерывность функции в точке. Свойства функций,
Непрерывных в точке.
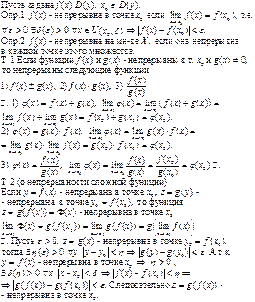
Классификация точек разрыва функции одной
Переменной.

Свойства функций, непрерывных на отрезке.

Обратная функция и ее непрерывность.

Определение производной. Геометрический и
Механический смысл производной.


Два определения дифференцируемой в точке
Функции и их эквивалентность. Дифференциал
Го порядка и его геометрический смысл.



Производные основных
Элементарных функций.

Правила дифференцирования.

Дифференцирование обратной и сложной функции.

§6. Метод логарифмического дифференцирования. 
Производные высших порядков. Бином Ньютона.

Дифференцирование функций,
Заданных параметрически.

Основные теоремы дифференциального
Исчисления.


Условия постоянства и монотонности функций
На интервале.

Экстремум функции. Необходимые и достаточные
Условия экстремума.

Наибольшее и наименьшее значения функции
На отрезке.
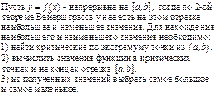
Выпуклость и вогнутость графика функции.
Точка перегиба.


Асимптоты графика функции. Полное
Исследование функции и построение ее графика.
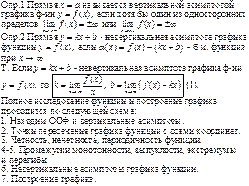
Раскрытие неопределенностей.
Правила Лопиталя.

Первообразная и неопределенный интеграл.
Свойства неопределенного интеграла.



Таблица основных интегралов.

Интегрирование по частям в неопределенном
Интеграле.

Замена переменной в неопределенном интеграле.

Интегрирование рациональных функций.


§6 Вычисление интегралов вида:


 §7. Интегрирование выражений вида
§7. Интегрирование выражений вида
. Подстановка Эйлера.

§8 Вычисление интегралов вида


Интегрирование тригонометрических функций.

Определение интеграла по Риману. Ограниченность
Интегрируемой функции.

Верхняя и нижняя интегральные суммы и их свойства.
Необходимые и достаточные условия интегрируемости
Функции по Риману.

Свойства неопределенного интеграла.







