Самоочищения оросительных каналов

 

Моделирование – это изучение объекта (оригинала) путем создания и исследования его копии (модели), замещающей оригинал с определенных сторон, интересующих познание. Модель всегда соответствует объекту – оригиналу – в тех свойствах, которые подлежат изучению, но в то же время отличается от него по ряду других признаков, что делает модель удобной для исследования интересующего нас объекта.

Модели, применяемые в обыденном научном познании, можно разделить на два больших класса: материальные и идеальные. Первые являются природными объектами, подчиняющимися в своем функционировании естественным законам. Вторые представляют собой идеальные образования, зафиксированные в соответствующей знаковой форме и функционирующие по законам логики, отражающей мир.

В области, которая может быть названа «моделированием, относящейся к исследованию тех или других физических явлений (в нашем случае – к исследованию движения жидкости), необходимо различать два совершенно различных вида моделирования: первый вид моделирования – физическое моделирование: в этом случае в модели воспроизводится изучаемое явления (оригинал, натура) с сохранением его физических свойств; например, в натуре мы имеем плотину, под которой фильтрует вода; модель здесь представляет собой плотину (созданную в некотором масштабе), под которой также фильтрует вода (физическое содержание процесса, имеющего место в натуре и на модели – одинакова: в порах грунта движется вода и в натуре, и на модели).

Второй вид моделирования – математическое моделирование: в этом случае исследование природных состояний или процессов выполняется путем изучения явлений, имеющих иное физическое содержание, однако описываемое теми же математическими зависимостями (которые описывают природные явления); примером такого моделирования может являться моделирование отмеченной выше плотины, когда фильтрация воды в ней изучается при помощи метода ЭГДА – электрогидродинамической аналогии (рис. 1) (23.С. 81-88).

 

Относящиеся к физическому моделированию

Гидравлические модели

Материальные (веществ.) модели могут быть выполнены: 1) В лаборатории 2) В полевых условиях и т.д.

Воображаемые (мысленные) модели могут быть описаны: 1) Чертежами, 2) словами 3) математическими знаками

Относящиеся к математическо-му моделиров

Относящиеся к физическому моделированию

Относящиеся к математическо-му моделиров.

ими

 

Здесь, обращаясь к модели рассматриваем не движение воды, а постоянный электрический ток, учитывая при этом, что и ламинарное движение воды (под плотиной в натуре) и электрический ток в соответствующей области подчиняются одному и тому же математическому уравнению – уравнению Лапласа.

К математическому моделированию следует отнести и расчет тех или других процессов, выполняемых по специально составленным программам на ЭВМ. Рассмотрим модель на примере моделирования извлечения органических веществ береговым биоплатом канала. Цель этой работы заключается в следующем: существует гидравлическая модель функционирования биоплата на канале, которая учитывает факторы площади поверхности и снижение концентрации ОВ в процессе их извлечения.

Предложенная модель демонстрирует математически строгий подход к этой проблеме, она позволяет исследовать гидродинамические характеристики движения воды в канале и зарослях тростника с учетом его замедляющего действия, а также влияние характеристик на диффузию примеси с учетом ее переноса потоком воды и поглощения тростником. Цель работы – оценка влияния характера течения в канале на скорость извлечения органической примеси. В работе гидравлической модели использовались два коэффициента шероховатости: один h₁ – для течения в основной части русла, свободной от растительности, а другой h₂ – для течения на поросшей тростником берме.

На рис. 2 показан профиль симметричного русла прямолинейного канала. Нулевая отметка на оси Х связана с плоскостью симметрии русла. Береговой склон бермы для удобства моделирования считался вертикальным, что, согласно и приведенным расчетам, незначительно повлияло на полученные профили скоростей и концентраций. Средние по времени скорости течения предполагались независящими от продольной координаты, а также от концентрации примеси.

 

 

 

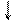
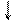
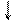
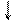
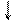
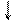
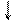
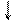
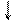
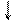
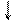
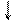
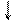
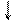
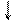
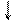
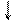
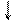
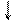
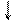
0 Х₁ 1 Х₂ Х₃ x,m

 

1 4,6

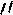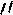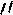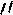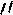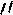2,3

 

h,m

Рис.2 Профиль расчетного канала

 

Расчет велся для d = 1см, N = 100м ^–2, n₁ = 0,025, Q = 3,1 м ³ с, чему соответствует гидравлический уклон Y = 0,0005

Коэффициент турбулентности вязкости а₁ полагался постоянным в области, свободной от тростника, и вычисляется по формуле, соответствующей вязкости в вертикальном направлении:

 

а₁ = R/М₁*С₁= Х/g*q

M₁ = 0,7C₁ + 6 при 10 = С₁ = 60

48 С > 60

где С₁ – коэффициент Шези части для русла свободной от тростника

М₁ – общий коэффициент.

В целях однородности вычислительной процедуры эта формула использовалась и для расчёта потока в части русла без растительности:

С₁ = 25 [ R / (80_n1)⁶ + ^0,025 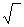RY ]^1/6

Определяем коэффициент шероховатости:

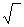H_{2 =} C_дdN * h₂^4/3 / 28

где d – средний диаметр одной тростинки;

H₂ – глубина на берме;

N – среднее число тростинок на квадратном метре бермы;

С_д = 1 – коэффициент их лобового сопротивления.

На рис. 3 изображён рассчитанный профиль средних скоростей в канале с параметрами, соответствующими водопроводному каналу средних размеров.

Точками обозначен профиль скоростей, полученный на физической напорной модели и пересчитанный на случай безнапорного течения в канале согласно известным принципам гидравлического моделирования. Физической моделью русла канала служил деревянный желоб, сечение которого было выполнено в масштабе 1:20 по вертикали и 1:30 по горизонтали.

 

V₁ м/с

 

1

0,5

1 2 3 4 4,6 х, м

 

 

Рис. 3. Эпюры средних скоростей течения в канале

1. – расчетная;

2. – по данным экспериментальных исследований;

3. – граница зарослей.

Тростник моделировался регулярно расположенными кусками нихромовой проволоки с соответствующей плотностью посадки, сверху желоб накрывался плоской стеклянной крышкой. Средняя скорость течения в эксперименте не соответствовала в точности расчетной, однако профиль осредненных по вертикали скоростей в такой модели можно считать с точностью до постоянного множителя не зависящим от средней скорости. Дальнейшие расчеты показали, что расчет извлекающий способности заросшей тростником бермы канала можно вести без учета профиля скоростей, зная лишь среднюю скорость течения в канале и извлекающую способность смоченной поверхности тростника. Таким образом моделирование играет огромную роль в процессах самоочищения оросительных каналов, что доказали результаты эксперимента.