—осто€ние однокомпонентных систем определ€ют две независимые переменные: давление и температура.
„исло степеней свободы равновесной термодинамической системы, на которую вли€ют только температура и давление, равно числу компонентов системы минус число фаз плюс 2, т.е. S = к Ц ф + 2 (по правилу фаз √иббса).
¬ однокомпонентной системе одновременно могут существовать три фазы: тверда€, жидка€ и парообразна€ и возможны следующие двухфазные равновеси€:
1) жидка€ фаза Ц тверда€ фаза
2) жидка€ фаза Ц пар
3) тверда€ фаза Ц пар
аждое из этих равновесий характеризуетс€ определенной кривой – = f(“). ѕоложение кривых определ€етс€ уравнением лапейрона Ц лаузиуса:
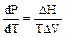
√рафическое изображение состо€ни€ равновесных фаз при разных температурах и давлени€х называетс€ диаграммой состо€ни€.
—осто€ние системы изображаетс€ частью плоскости, котора€ называетс€ фазовым полем.
‘азовое поле Ц геометрическое место точек, изображающих различные состо€ни€ одной и той же фазы.
‘азовые пол€ разделены фазовыми лини€ми.
ƒиаграмма состо€ни€ воды
 |
–исунок 3. ƒиаграмма состо€ни€ воды
|
„исло степеней свободы в этой точке определ€етс€ по формуле S = к Ц ф + 2 = 1 Ц 3 + 2 = 0.
≈сли изменить в этой точке одну из переменных, то исчезнет одна из фаз. Ќапример, если увеличить температуру, то исчезнет тверда€ фаза. ѕока исчезает тверда€ фаза, температура не изменитс€.
ѕосле исчезновени€ твердой фазы останетс€ двухфазна€ система жидкость Ц пар. ќна моновариантна т.е. S = 1 Ц 2 + 2 = 1.
—ледовательно, изображаетс€ фазовой линией.
Ћини€ ќ— отображает равновесие жидкость Ц пар. ¬ этой системе можно мен€ть либо давление, либо температуру. ≈сли увеличить температуру, то давление будет увеличиватьс€ и фигуративна€ точка будет двигатьс€ вверх по кривой ќ—. “очка — Ц это критическа€ точка, выше которой жидкость не может существовать, т.к. “ = 647,35 ; – = 221,406 ѕа.
Ћинию ќ— можно продолжить в обратную сторону за тройную точку ќ (лини€ ќƒ). ќна соответствует равновесию пар Ц переохлажденна€ жидкость, т.е. показывает давление пара над переохлажденной водой. ќно всегда выше, чем давление пара надо льдом. ѕоэтому переохлажденна€ вода €вл€етс€ неустойчивой (метастабильной) фазой относительно льда, который в этой области температур устойчив.
ѕри понижении температуры (в точке ќ) исчезает жидкость. —истема станет двухфазной: лед Ц пар, моновариантной (крива€ јќ). Ћини€ ќ¬ соответствует кривой плавлени€ (или кристаллизации).
„исло степеней свободы в любой точке, принадлежащей какой-либо фазовой линии, отражающей двух фазное равновесие, равно 1, т.е. S = 1 Ц 2 + 2 = 1.
Ёто значит, чтобы в системе сохран€лось равновесие, можно изменить лишь один из параметров (либо температуру, либо давление).
«ависимость давлени€ от температуры описываетс€ уравнением лаузиуса Ц лапейрона.
|
|
|
–ассмотрим конкретные случаи его применени€.
 а) –авновесие жидкость пар; DЌисп > 0,
а) –авновесие жидкость пар; DЌисп > 0,
тогда 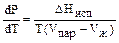
“ак как удельный мольный объем пара больше соответствующего объема жидкости, т.е. Vп >Vж, то 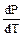 и значит
и значит 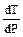 всегда положительна. —ледовательно, температура испарени€ всегда повышаетс€ с ростом давлени€. ¬еличина
всегда положительна. —ледовательно, температура испарени€ всегда повышаетс€ с ростом давлени€. ¬еличина 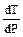 отражает наклон кривой и показывает изменение температуры с увеличением давлени€.
отражает наклон кривой и показывает изменение температуры с увеличением давлени€.
 б) –авновесие твердое жидкость; DЌпл (крива€ ќ¬)
б) –авновесие твердое жидкость; DЌпл (крива€ ќ¬)
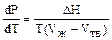 ; DV = (Vж Ц Vтв) Ц очень мала
; DV = (Vж Ц Vтв) Ц очень мала
—ледовательно, 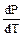 очень велика и крива€ равновеси€ твердое тело Ц жидкость (ќ¬) идет круто вверх.
очень велика и крива€ равновеси€ твердое тело Ц жидкость (ќ¬) идет круто вверх.
—ледует обратить внимание, что дл€ таких веществ, как вода, висмут, галлий в твердом состо€нии имеют плотность меньше, чем в охлажденном состо€нии.
ƒл€ них Vж >Vтв, т.е. Vж Ц Vтв < 0
ѕоэтому производна€ отрицательна и крива€ плавлени€ наклонена несколько влево.
ƒиаграмма состо€ни€ серы
¬ однокомпонентных системах может быть только одна парова€ и одна жидка€ фаза, а твердых фаз может быть несколько. ” серы, например, существует две модификации: ромбическа€ Sромб и моноклинна€ Sмонокл (рисунок 4).
 |
–ис. 4. ƒиаграмма состо€ни€ серы
|
ѕри нагревании обычной серы выше 95,50— она постепенно превращаетс€ в моноклинную Sмонокл
“аким образом, число возможных фаз дл€ серы равно 4: ромбическа€ (тверда€), моноклинна€ (тверда€), жидка€ и парообразна€.
—плошные линии дел€т диаграмму на четыре области:
область выше ƒј¬≈ Ц однофазна€ область ромбической твердой серы;
ј¬— Ц однофазна€ область твердой моноклинической серы;
EBCF Ц однофазна€ область серы в жидком состо€нии;
область ниже ƒј—F Ц однофазна€ область парообразной серы.
ажда€ крива€ этой диаграммы отражает соответствующие фазовые равновеси€:
 ј¬ Ц Sромб Sмонокл
ј¬ Ц Sромб Sмонокл
¬— Ц Sмонокл Sжид
ј— Ц Sмонокл Sпар
јƒ Ц Sромб Sпар
¬≈ Ц Sромб Sжид
CF Ц Sжид Sпар
 ¬ точке ј: Sромб Sмонокл Sпар
¬ точке ј: Sромб Sмонокл Sпар
¬: Sромб Sмонокл Sжид
—: Sмонокл Sжид Sпар
„исло степеней свободы в этих точках равно 0: S = 1 Ц 3 + 2 = 0
ѕредполагаема€ четверта€ точка, отвечающа€ равновесию
 Sмонокл Sжид Sпар
Sмонокл Sжид Sпар
практически трудно осуществимо, т.к. это равновесие метастабильное.
–авновесие всех четырех фаз
 Sромб Sмонокл Sжид Sпар
Sромб Sмонокл Sжид Sпар
не может быть осуществимо ни при каких услови€х, т.к. правило фаз дл€ этого равновеси€ приводит к отрицательному числу степеней свободы:
S = 1 Ц 4 + 2 = Ц 1
 »так, сера при нагревании может превращатьс€ из ромбической в моноклинную. ¬озможен и обратный процесс, т.е. при охлаждении переход серы из моноклинной в ромбическую Sмонокл Sромб.
»так, сера при нагревании может превращатьс€ из ромбической в моноклинную. ¬озможен и обратный процесс, т.е. при охлаждении переход серы из моноклинной в ромбическую Sмонокл Sромб.
“аким образом, взаимные превращени€ одной кристаллической формы серы в другую протекает обратимо.
≈сли данна€ модификаци€ кристаллического вещества обладает свойством при изменении внешних условий (например, температуры) переходить в другую модификацию и при восстановлении прежних условий возвращатьс€ в первоначальную модификацию, то такие полиморфные превращени€ называютс€ энантиотропными).
ѕримером энантиотропного фазового перехода может служить процесс взаимного перехода серы ромбической и серы моноклинической.
ѕревращени€ модификаций, которые могут протекать в одном направлении называютс€ монотропными (бензофенон).
|
|
|
ƒвухкомпонентные системы
ѕри изучении систем, состо€щих их двух компонентов, используетс€ метод графического изображени€ зависимости какого-либо свойства раствора от его концентрации.
“акое графическое изображение называют диаграммой состав Ц свойство.
ќбычно диаграмма должна укладыватьс€ на плоскость, ограниченную ос€ми ординат и абсцисс (рисунок 5).

–ис. 5. ƒиаграмма состав Ц свойство
Ќа оси ординат откладываетс€ любое свойство (температура, давление, плотность, показатель преломлени€ и т.д.).
Ќа оси абсцисс откладывают состав бинарной смеси, который может быть выражен в мольных дол€х или в процентах.
Ћева€ точка ј соответствует 100%-му содержанию компонента ј, права€ точка ¬ соответствует 100%-му содержанию компонента ¬. ѕромежуточные точки между ј и ¬ соответствуют смес€м, состо€щим из двух компонентов. ѕо мере удалени€ от точки ј уменьшаетс€ содержание компонента ј, но возрастает содержание компонента ¬.
|
≈сли смешать какие-либо две жидкости, которые ограниченно растворимы друг в друге, то через некоторое врем€ произойдет расслоение и получитс€ система, состо€ща€ из двух сопр€женных растворов, наход€щихс€ в равновесии. ќдин из них представл€ет собой раствор первой жидкости во второй, другой Ц раствор второй жидкости в первой.
—одержание обоих жидкостей в этих двух сопр€женных растворах зависит от состава и от температуры. ѕри некотором соотношении компонентов и при определенной температуре может наблюдатьс€ полна€ взаимна€ растворимость жидкостей.
ƒл€ изображени€ зависимости взаимной растворимости жидкостей от температуры при посто€нном давлении стро€т диаграмму состо€ни€ в координатах температура Ц состав, котора€ называетс€ диаграммой растворимости.






