Нормальные системы обыкновенных дифференциальных уравнений.
Определение. Совокупность соотношений вида:
где х - независимая переменная, у1, у2,…,уn – искомые функции, называется системой дифференциальных уравнений первого порядка.
Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.
Такая система имеет вид:
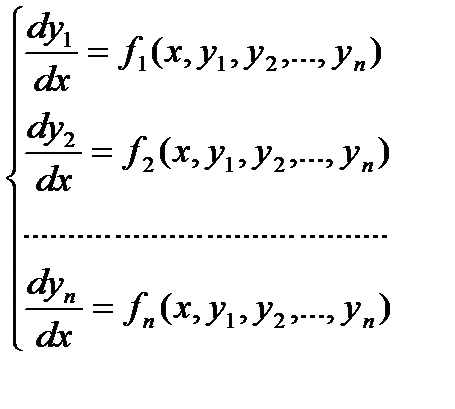(1)
Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.
Теорема. (Теорема Коши). Если в некоторой области (n-1) –мерного пространства функции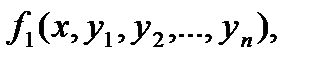 
… 
непрерывны и имеют непрерывные частные производные по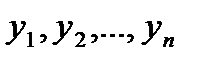 
, то для любой точки 
этой области существует единственное решение
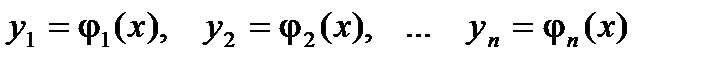
системы дифференциальных уравнений вида (1), определенное в некоторой окрестности точки х0 и удовлетворяющее начальным условиям 
Определение. Общим решением системы дифференциальных уравнений вида (1) будет совокупность функций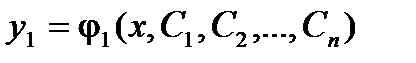 
, 
, … 
, которые при подстановке в систему (1) обращают ее в тождество.
П.1. Нормальные системы линейных однородных дифференциальных
уравнений с постоянными коэффициентами.
При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.
Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:
(2)
Решения системы (2) обладают следующими свойствами:
1) Если y, z, u – решения системы, то Cy, Cz, Cu, где C = const – тоже являются решениями этой системы.
2) Если y1, z1, u1 и y2, z2, u2 – решения системы, то y1 + y2, z1 + z2, u1 + u2 – тоже являются решениями системы.
Решения системы ищутся в виде: 
Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на ekx, получаем:
Для того чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.:
В результате вычисления определителя получаем уравнение третьей степени относительно k. Это уравнение называется характеристическим уравнением и имеет три корня k1, k2, k3. Каждому из этих корней соответствует ненулевое решение системы (2):
Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):
Пример 1. Найти общее решение системы уравнений:
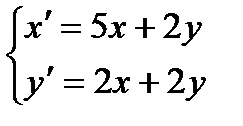
Решение. Составим характеристическое уравнение:
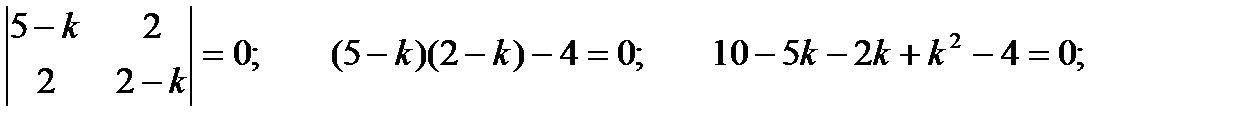
Решим систему уравнений:
Для k1: 
Полагая 
(принимается любое значение), получаем: 
Для k2: 
Полагая 
(принимается любое значение), получаем: 
Общее решение системы: 
Этот пример может быть решен другим способом:
Решение. Продифференцируем первое уравнение: 
Подставим в это выражение производную у¢ = 2 x + 2 y из второго уравнения.
Подставим сюда у, выраженное из первого уравнения: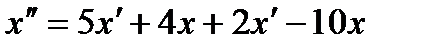 
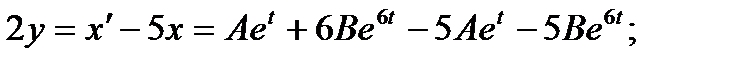
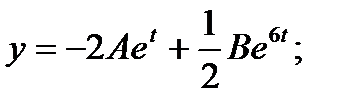
Обозначив 
, получаем решение системы:
Пример 2. Найти решение системы уравнений
Решение. Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т.к. не является однородным (в уравнение входит независимая переменная х).
Для решения продифференцируем первое уравнение по х. Получаем: 
Заменяя значение z’ из второго уравнения получаем: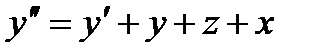 
.
С учетом первого уравнения, получаем: 
Решаем полученное дифференциальное уравнение второго порядка.
Общее решение однородного уравнения: 
Теперь находим частное решение неоднородного дифференциального уравнения по формуле 
Общее решение неоднородного уравнения: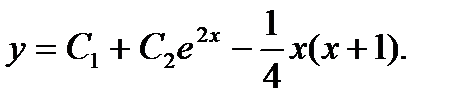 
Подставив полученное значение в первое уравнение системы, получаем:
Пример 3. Найти решение системы уравнений: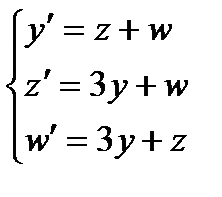 
Решение. Составим характеристическое уравнение:
1) k = -1.
Если принять g = 1, то решения в этом случае получаем:
2) k2 = -2.
Если принять g = 1, то получаем:
3) k3 = 3.
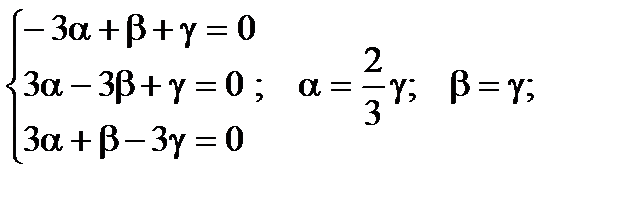
Если принять g = 3, то получаем:
Общее решение имеет вид:
Пример 4. Найти частное решение системы уравнений, удовлетворяющее начальным
условиям: 
Примеры. Найти решение систем уравнений:
Пример. Найти частное решение системы уравнений, удовлетворяющее начальным
условиям:
Пример. Найти решение системы уравнений:
