МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Информатика и программное обеспечение»
КУРСОВАЯ РАБОТА
по курсу
«ИНФОРМАТИКА»
Тема: «Решение задач вычислительной математики с помощью программ Excel и Mathcad»
Выполнил ст. гр. 11-КТО2
___________Бородынкин А. Д.
Проверил:
_______доц. Азарченков А.А.
БРЯНСК 2012
Оглавление
Введение. 3
Задание №1.. 6
1.1. Условие задачи.. 6
1.2. Решение в Mathcad.. 6
1.3. Решение в Excel 7
Задание №2.. 10
2.1. Условие задачи.. 10
2.2. Решение в Mathcad.. 10
2.3. Решение в Excel 10
Задание №3.. 13
3.1. Условие задачи.. 13
3.2. Решение в Mathcad.. 13
3.3. Решение в Excel 14
Задание №4.. 16
4.1. Условие задачи.. 16
4.2. Решение в Mathcad.. 16
4.3. Решение в Excel 20
Задание №5.. 23
5.1. Условие задачи.. 23
5.2. Решение в Mathcad.. 23
5.3. Решение в Excel 23
Заключение. 26
Список использованный литературы... 27
Введение
Предназначение пакета Excel.
Программа excel создана специально для работы с электронными таблицами корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS. В этой программе можно производить экономико-статистические расчеты, строить диаграммы, автоматизировать расчетную деятельность, как бухгалтерского характера, так и инженерно-технического, а также обрабатывать большие массивы данных, визуализируя их с помощью графических элементов.
Каждый офисный работник без всяких промедлений может ответить вам, для чего нужен Excel, поскольку большую часть рабочего времени проводит в этой программе. Чтобы найти работу на рынке труда, в большинстве случаев требуют от потенциальных работников умение пользоваться персональным компьютером, а также свободно пользоваться таким программным продуктом, как Excel, поскольку большинство подотчетной документации готовиться именно в нем. Таблицы, которые создаются в этой программе, можно с легкостью открывать и редактировать или же просто вставлять в необходимые документы, только с тем условие, чтобы они поддерживали этот продукт.
Предназначение пакета Mathcad.
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Corporation).
Mathcad имеет простой и интуитивный для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.
Некоторые из математических возможностей Mathcad (версии до 13.1 включительно) основаны на подмножестве системы компьютерной алгебры Maple (MKM, Maple Kernel Mathsoft). Начиная с 14 версии — использует символьное ядро MuPAD.
Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий.NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).
Задание №1
Условие задачи
Дано нелинейное уравнение вида f(x)=0. Решить заданное нелинейное уравнение с помощью программ Excel и Mathcad.
Решение в Mathcad
1) С помощью программы Mathcad построим график функции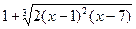 
на интервале [-5;15] (рис.1. 1). По графику определяем приближенные значения корней уравнения 0.8, 1.4 и 7.
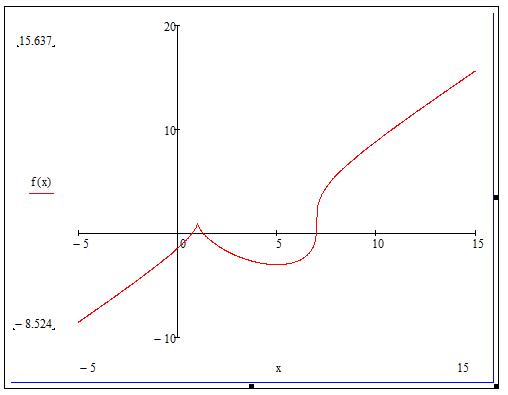
Рис.1. 1. График функции f(x), построенный в Mathcad
2) С помощью функции root находим точные значения корней уравнения x1=0.7181; x2=1.29645; x3=6.98605.
3) Используя символьные вычисления Mathcad, найдем производную
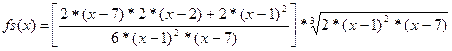
4) Построим график производной функции f(x). По графику определяем приближенное значение корней fs(x)=0: x=5; x=0.9. С помощью функции root находим точное значение первого корня уравнения fs(x)=0. Второй корень находим с помощью функции «maximize», так как при х=1 производная функции не существует. Получили следующие значения экстремумов: xmin = 5; xmax = 1 (рис.1. 2).
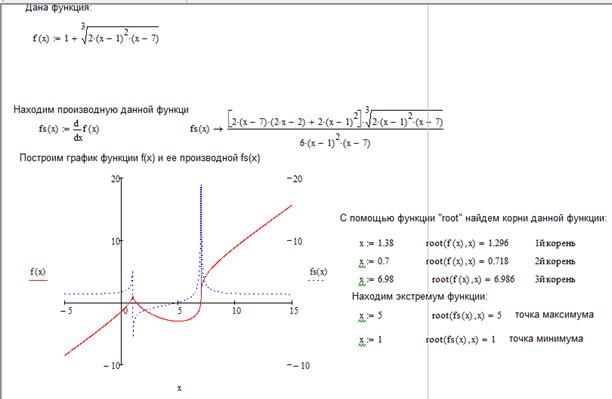
Рис.1. 2. Нахождение корней уравнения и экстремумы функции при помощи Mathcad
Решение в Excel
5) Выполним табулирование функции 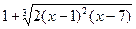в Excel на интервале [-5;15] с шагом 0,2.
6) На основе полученной таблицы табуляции строим график функции f(x) (рис.1. 3).
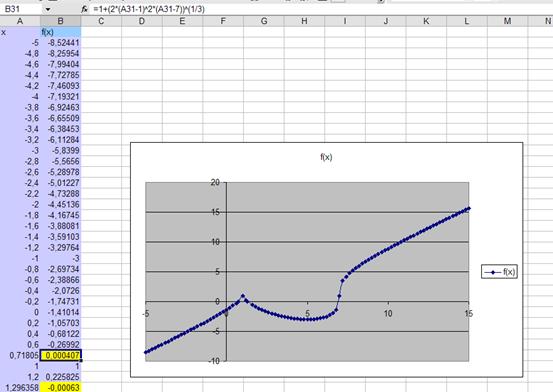
Рис.1. 3. Табуляция функции и построение графика в Excel
7) На полученном графике определяем приближенные значения корней уравнения. Данные корни будут находиться в точках пересечения графика функции с осью абсцисс, а также их приближенные значения можно определить по таблице табуляции в строках, где значения в столбце y меняют свой знак. Получаем следующие приближенные значения корней уравнения: 0,8; 1,4 и 7. С помощью процедуры «Подбор параметра» определяем точное значение корня для каждого приближенного значения. Получаем следующие значение корней уравнения: x1=0,71805; x2=1,29636; x3=6,98604 (рис.1. 4).
Рис.1. 4. Фрагмент листа Excel с найденными корнями уравнения
8) Найдем в Excel экстремумы функции f(x). По графику видно, что данная функция имеет две точки экстремума (максимум и минимум) в районе x=1 и x=5. Скопируем данные из таблицы табуляции для поиска максимума и минимума. Для нахождения этих экстремумов, воспользуемся надстройкой «Поиск решения» и настроим ее согласно рис.1. 5. Отсюда видно, что xmin=5; xmax=1.
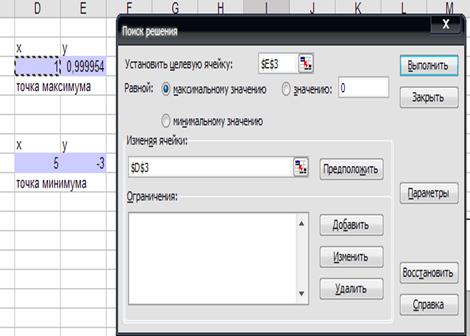
Рис.1. 5. Настройка «Поиска решения» для задачи нахождения экстремумов
Задание №2
Условие задачи
Даны матрицы A, B и С.
, 
, 
.
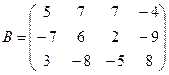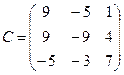Вычислить матрицу D по формуле согласно варианту (прил.2). Задание выполнить в Excel и Mathcad.
Решение в Mathcad
1) Расчет матрицы D средствами Mathcad показан на рис.2. 1
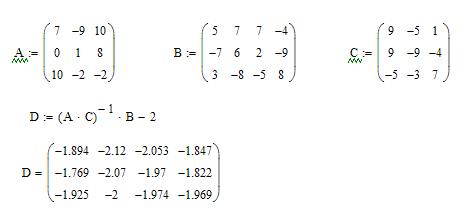
Рис.2. 1. Вычисление матрицы D в Mathcad
Решение в Excel
2) Вычислим значение матрицы D по формуле: D=A*B+5*C^T c помощью Excel. (Рис.2. 2)
Рис.2. 2. Вычисление матрицы D в Excel
Задание №3
Условие задачи
Используя коэффициенты полученной матрицы D, решить систему следующих нелинейных уравнений:
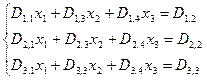
Решение в Mathcad
1) Решение системы уравнений в Mathcad приведено на рис.3. 1
Рис.3. 1. Решение системы уравнений с помощью Mathcad
Решение в Excel
2) Решим следующую систему линейных уравнений, используя коэффициенты из полученной матрицы D в Excel с применением последовательности операций линейной алгебры, а именно – с применением обратной матрицы (рис.3. 2 ). В результате получили вектор решения:
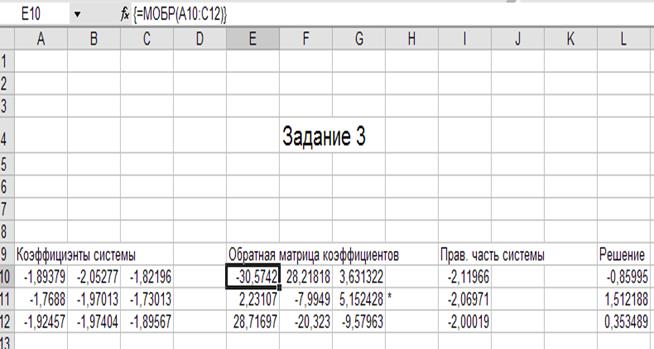
Рис.3. 2. Решение системы нелинейных уравнений с помощью Excel
Задание №4
Условие задачи
Ø С помощью программы Mathcad провести кусочно-линейную интерполяцию и найти значения y для следующих значений x: 1.3, 2.6, 4.4, 5.9, 7.1, 8.75. Построить график.
Ø С помощью программы Mathcad провести полиномиальную интерполяцию и найти значения y для следующих значений x: 1.3, 2.6, 4.4, 5.9, 7.1, 8.75. Построить график. Записать уравнение полинома (коэффициенты полинома указать с точностью 10 знаков после запятой)
Ø Провести 2 вида аппроксимации: (полином 5-й степени и линейная функция). Построить оба графика на одной координатной плоскости. В обоих случаях определить сумму квадратов отклонений для узловых точек. Данное задание выполнить как в Excel, так и в Mathcad.
Выполним это задание для следующих точек:
| x | 0.01 | |||||||||
| y | -7.36 | -3.87 | 24.94 | 5.94 | 42.2 | 35.7 | -0.91 | 24.72 | -24.42 | 29.2 |
Решение в Mathcad
1) Проведем кусочно-линейную интерполяцию с помощью функции «linterp» для заданных точек и определяем значение функции для указанных значений аргумента (рис.4. 1):
| x | 1.3 | 2.6 | 4.4 | 5.9 | 7.1 | 8.75 |
| y | 4.773 | 13.54 | 39.6 | 2.751 | 19.806 | 15.795 |
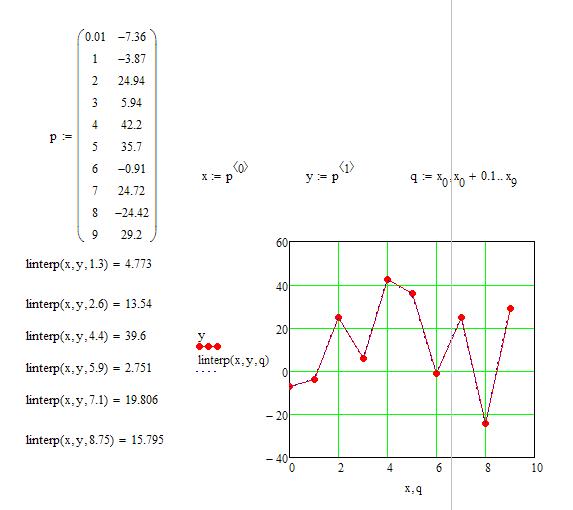
Рис.4. 1. Кусочно-линейная интерполяция в Mathcad
2) Проведем полиномиальную интерполяцию с помощью функции «regress». Учитывая, что задано 10 точек, то полином должен быть 9-й степени. В результате получили полином, представленный на рис.4. 2. Построим его график, на котором отметим исходные точки (рис.4. 1). По графику можно убедиться, что полином проходит через все заданные точки.
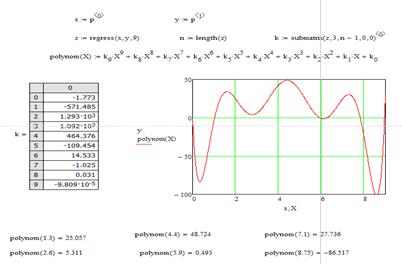
Рис.4. 2. Полиномиальная интерполяция в Mathcad
3) Используя функцию «polynom», определим для заданных точек значение функции (рис.4. 2):
| x | 1.3 | 2.6 | 4.4 | 5.9 | 7.1 | 8.75 |
| y | 25.057 | 5.311 | 48.724 | 0.493 | 27.736 | -86.517 |
4) Проведем с помощью Mathcad аппроксимацию для заданных точек с помощью полинома 5-й степени и линейной функции. Вторая есть полином 1-й степени, потому расчеты будут похожи (рис.4. 3). Определим сумму квадратов отклонений для узловых точек (рис.4. 3):
· Для полинома 5-й степени эта величина равна 1881.
· Для линейной функции эта величина равна 4177.
5) Можно сделать вывод, что с помощью полинома 5-й степени мы получаем более точное приближение.
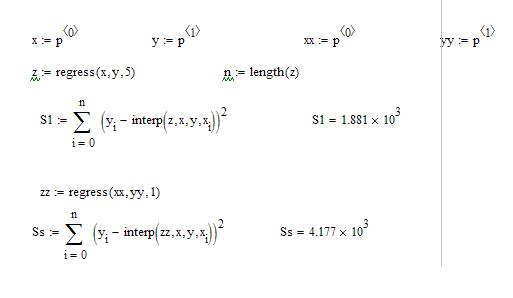
Рис.4. 3. Аппроксимация точек в Mathcad
6) Построим на одной координатной плоскости графики аппроксимирующих функций (рис.4. 4).
Рис.4. 4. Графики аппроксимирующих функций
Решение в Excel
7) Проведем аппроксимацию точек с помощью Excel. Для этого сначала заполним исходную таблицу точек и отметим эти точки на графике (рис.4. 5).
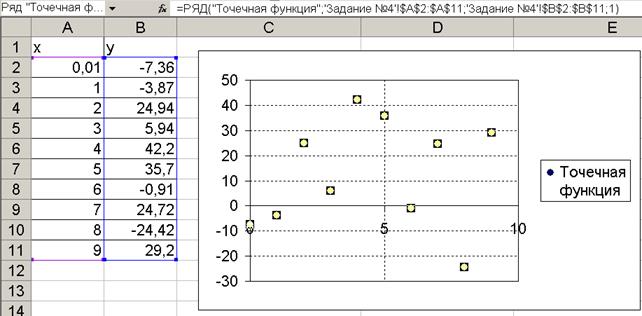
Рис.4. 5. Исходные точки для аппроксимации на графике
8) Вызовем контекстное меню для одной из точек на графике и выберем пункт «Добавить линию тренда…». Для начала проведем аппроксимацию с помощью полинома 5-й степени. Для этого в открывшемся диалоговом окне «Линия тренда» выберем «Полиномиальная» и укажем степень «5».
9) Аналогично добавим линию тренда на основе линейной функции. В настройках линий тренда выставим галочку «показывать уравнение на диаграмме». Результат представлен на рис.4. 6. Получили следующие аппроксимирующие функции:
· Для полинома 5-й степени:
· Для линейной функции:
Рис.4. 6.Получение графиков функций апроксимации
10) Определим сумму квадратов отклонений для полученных функций в узловых точках (рис.4. 7). Получим:
· Для полинома 5-й степени эта величина равна 1882,9.
· Для линейной функции эта величина равна 4176,8.
Следовательно, аппроксимация набора данных полинома 5-й степени более точна, чем линейной функции.
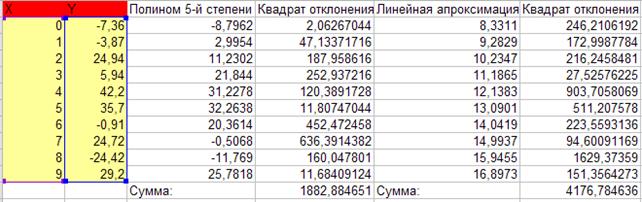
Рис.4. 7. Расчет в Excel суммы квадратов отклонений для аппроксимирующих функций
Задание №5
Условие задачи
Найти экстремум функции двух переменных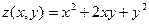 
в Excel и Mathcad. Построить график двумерной поверхности в Excel и Mathcad. Сравнить результаты и сделать выводы.
Решение в Mathcad
1) Построим график функции в Mathcad ( рис.5. 1)
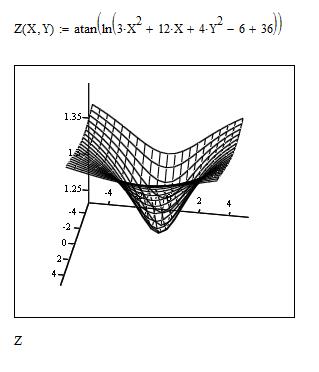
Рис.5. 1. Построение поверхность в Mathcad
2) По графику определяем, что функция z имеет множество точек минимума, которые располагаются в пересечении значений x и у с разными знаками.
3) Воспользуемся блоком решения Mathcad и функцией Minimize. За начальное приближение точки минимума возьмем x=0 и y=0. В качестве ограничений укажем интервалы для xÎ[-4;4] и yÎ[-4;4]. Также можно взять любую пару точек (х; у), но с разными знаками.
4) Получили решение x=0; y=0 (рис.5. 2).
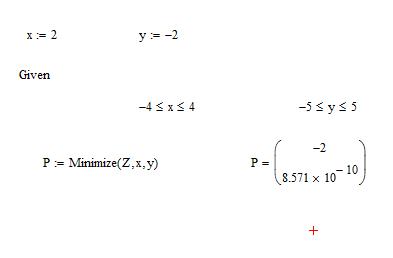
Рис.5. 2. Минимизация функции в Mathcad
Решение в Excel
5) Для выполнения сначала проведем табуляцию функции с шагом 0,5 на интервале по xÎ[-4;4] и yÎ[-4;4] (рис.5. 3).
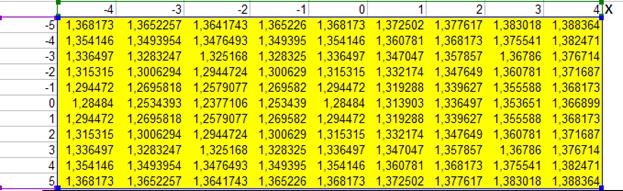
Рис.5. 3. Табулирование функции 2-х переменных в Excel
6) На основе полученной таблицы строим поверхность (рис.5. 4).
Рис.5. 4. График функции 2-х переменных в Excel
7) С помощью надстройки «Поиск решения» найдем точку минимума. Для этого настроим соответствующее диалоговое окно следующим образом (рис.5. 5). В результате выполнения получим искомую точку минимума: x=0; y=0 (рис.5. 5). Также отмечаем всю диагональ, значения которой равны 0.
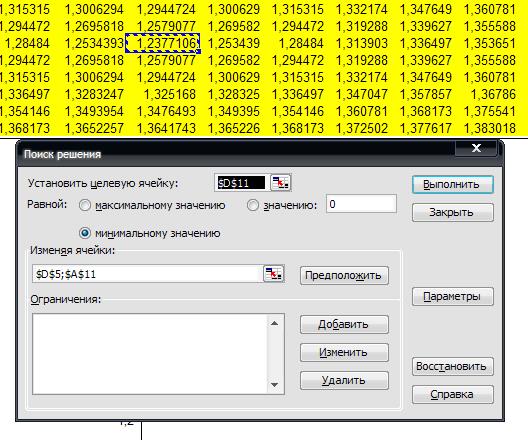
Рис.5. 5. Настройка «Поиска решения» для задачи нахождения минимума
Заключение
В ходе выполнения данной курсовой работы, мне удалось узнать многие новые, ранее мне неизвестные возможности пакетов Excel и Mathcad. Я понял, что данные программы очень полезны и многофункциональны, являются очень популярными в использовании в разных областях. Создавая курсовую работу, осуществляется изучение систем связанных электронных таблиц, включая конструирование и трассировку связей между таблицами, внедрение диаграмм в расчетные листы, овладение навыками редактирования и оформления электронных табличных расчетов. В ходе курсового проектирования проведено: исследование нелинейной функции одной переменной, основные операции с матрицами, решение системы линейных уравнений, приближение таблично заданной функции, экстремум функции двух переменных.
Список использованный литературы
1. Зернин, М.В., Коростелёв, Д.А. Информатика. Решение инженерно-математических задач с помощью программ Excel и Mathcad: методические указания к выполнению курсовой работы для студентов очной формы обучения технических специальностей. – Брянск: БГТУ, 2011 – 55с.
2. А. С. Грошев. Информатика. Учебник для вузов. — Архангельск: Арханг. гос. техн. ун-т, 2010. — 470 с. — ISBN 978-5-261-00480-6
3. Дж. Гленн Брукшир. Введение в компьютерные науки = Computer Science: An Overview. — 6-е изд. — М.: Вильямс, 2001. — 688 с. — ISBN 5-8459-0179-0
4. Глушков В. М. Безбумажная информатика. — М.: Наука, 1978.
5.
